Алгоритмы / Алгоритм Дейкстры

1. Алгоритм Дейкстры (Нахождение кратчайших путей от выделенной вершины до всех остальных вершин графа)

Алгоритм Дейкстры – алгоритм на графах, который находит кратчайший путь между двумя данными вершинами в графе с неотрицательными длинами дуг. Также часто ставится задача расчёта кратчайшего пути от данной вершины до всех остальных. Алгоритм широко применяется в программировании, например, его используют протоколы маршрутизации.

Описание

На вход алгоритма подаётся взвешенный ориентированный граф с дугами неотрицательного веса. На выходе получается набор кратчайших путей от данной вершины до других.

В начале расстояние для начальной вершины полагается равным нулю, а расстояния до всех остальных понимаются бесконечными. Массив флагов, обозначающих то, пройдена ли вершина, заполняется нулями. Затем на каждом шаге цикла ищется вершина с минимальным расстоянием до изначальной и флагом равным нулю. Для неё устанавливается флаг и проверяются все соседние вершины. Если рассчитанное ранее расстояние от исходной вершины до проверяемой больше, чем сумма расстояния до текущей вершины и длины ребра от неё до проверяемой вершины, то расстояние до проверяемой вершины приравниваем к расстоянию до текущей+ребро от текущей до проверяемой. Цикл завершается, когда флаги всех вершин становятся равны 1, либо когда расстояние до всех вершин c флагом 0 бесконечно. Последний случай возможен тогда и только тогда, когда граф несвязеный.

Алгоритм Дейкстры в псевдокоде

Вход: С : array [l..p, l..p] of real – матрица длин дуг графа; s – вершина, от которой ищется кратчайший путь и t – вершина, к которой он ищется.

Выход: векторы Т : array [l..p] of real; и Н : array [l..p] of 0..р. Если вершина v лежит на кратчайшем пути от s к t, то T[v] — длина кратчайшего пути от s к у; Н[у] — вершина, непосредственно предшествующая у на кратчайшем пути.

Н – массив, в котором вершине n соответствует вершина m, предыдущая на пути к n от s.

T – массив, в котором вершине n соответствует расстояние от неё до s.

X – массив, в котором вершине n соответствует 1, если путь до неё известен, и 0, если нет.

инициализация массивов:

for v from 1 to р do

Т[v]: = ∞ { кратчайший путь неизвестен }

X[v]: = 0 { все вершины не отмечены}

end for

H[s]: = 0 { s ничего не предшествует }

T[s]: = 0 { кратчайший путь имеет длину 0...}

X[s]: = 1 { ...и он известен } v: = s { текущая вершина }

поиск:

М: { обновление пометок }

for и ∈ Г(и) do

if Х[и] = 0 & Т[и] > T[v] + C[v, u] then

Т[и]: = T[v] + C[v, и] { найден более короткий путь из s в и через v}

H[u]: = v { запоминаем его }

end if

end for

m: = ∞

v : = 0

{ поиск конца кратчайшего пути }

for и from 1 to p do

if X[u] = 0 &T[u] < t then

v: = u;

m: = T[u] { вершина v заканчивает кратчайший путь из s

end if

end for

if v = 0 then

stop { нет пути из s в t} end if

if v = t then

stop { найден кратчайший путь из s в t} end if

X[v]: = 1 { найден кратчайший путь из s в v } goto M

Обоснование

Для доказательства корректности алгоритма Дейкстры достаточно заметить, что при каждом выполнении тела цикла, начинающегося меткой М, в качестве v используется вершина, для которой известен кратчайший путь из вершины s. Другими словами, если X[v] = 1, то T[v] = d(s,v), и все вершины на пути (s,v), определяемом вектором Н, обладают тем же свойством, то есть

Vu Т[и] = 1 => Т[и] = d(s,u)&T[H[u]] = 1.

Действительно (по индукции), первый раз в качестве v используется вершина s, для которой кратчайший путь пустой и имеет длину 0 (непустые пути не могут быть короче, потому что длины дуг неотрицательны). Пусть Т[u] = d(s,u) для всех ранее помеченных вершин и. Рассмотрим вновь помеченную вершину v, которая выбрана из условия T[v] = min Т[и]. Заметим, что если известен путь, проходящий через помеченные вершины, то тем самым известен кратчайший путь. Допустим (от противного), что T[v] > d(s, v), то есть найденный путь, ведущий из s в v, не является кратчайшим. Тогда на этом пути должны быть непомеченные вершины. Рассмотрим первую вершину w на этом пути, такую что T[w] = 0. Имеем: T[w] = d(s,w) ⩽ d(s>v) < Т[v], что противоречит выбору вершины u.

Временная сложность

Сложность алгоритма Дейкстры зависит от способа нахождения не посещённой вершины с минимальным расстоянием до изначальной, способа хранения множества непосещённых вершин и способа обновления меток. Пусть n количество вершин, а через m — количество рёбер в графе. Тогда в простейшем случае, когда для поиска вершины с минимальным расстоянием до изначальной вершины просматривается всё множество вершин, а для хранения расстояний используется массив, время работы алгоритма - О(n²). Основной цикл выполняется порядка n раз, в каждом из них на нахождение минимума тратится порядка n операций. На циклы по соседям каждой посещаемой вершины тратится количество операций, пропорциональное количеству рёбер m (поскольку каждое ребро встречается в этих циклах ровно дважды и требует константное число операций). Таким образом, общее время работы алгоритма O(n²+m), но, так как m много меньше n(n-1), в конечном счёте получается О(n²).

Для разреженных графов (то есть таких, для которых m много меньше n²) непосещённые вершины можно хранить в двоичной куче, а в качестве ключа использовать значения расстояний. Так как цикл выполняется порядка n раз, а количество релаксаций (смен меток) не больше m, время работы такой реализации — О(nlogn+mlogn)

Пример

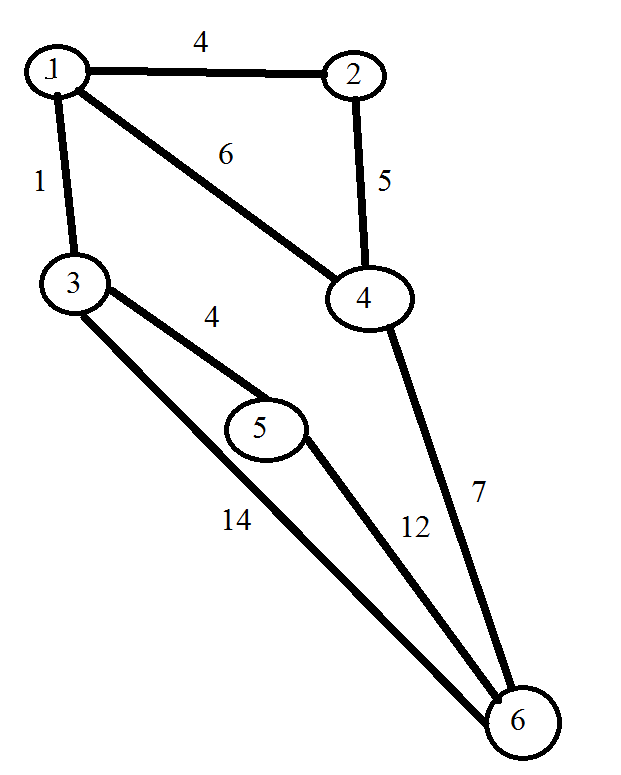
	1	2	3	4	5	6
1	0	4	1	6	∞	∞
2	4	0	∞	5	∞	∞
3	1	∞	0	∞	4	14
4	6	5	∞	0	∞	7
5	∞	∞	4	∞	0	12
6	∞	∞	14	7	12	0

Вычисление расстояний от вершины 1 по проходимым вершинам:

	1	2	3	4	5	6
1	0	4	1	6	∞	∞
3	0	4	1	6	5	15
2	0	4	1	6	5	15
5	0	4	1	6	5	15
4	0	1	4	6	5	13
6	0	1	4	6	5	13