Теорема. R(sin X, cos X) интегрируема в элементарных функциях.

Доказательство. Введем новую переменную .

Это универсальная тригонометрическая подстановка.

..

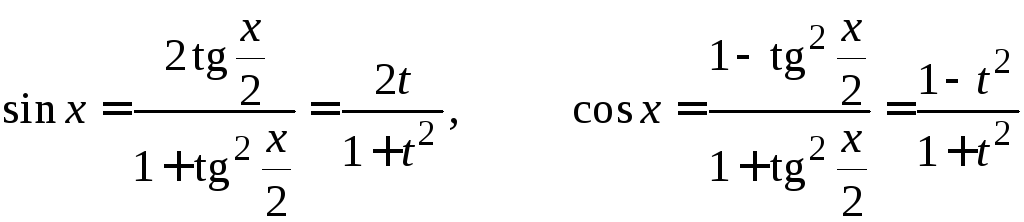Поэтому .

Получен интеграл от рациональной функции имеет элементарную первообразную, в которую подставим

Пример..

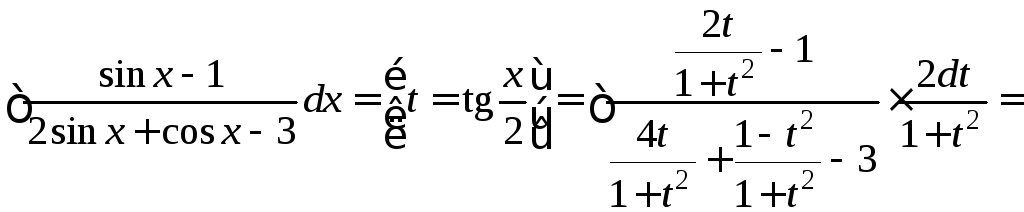
Определение. Подстановку, превращающую интеграл в интеграл от рациональной функции будем называть рационализирующей подстановкой для рассматриваемого интеграла.

Замечание. Часто другие подстановки дают более короткие решения. Например:

а) .

б).

в)

 или.

При этом, ,

.

Пример. =

= .

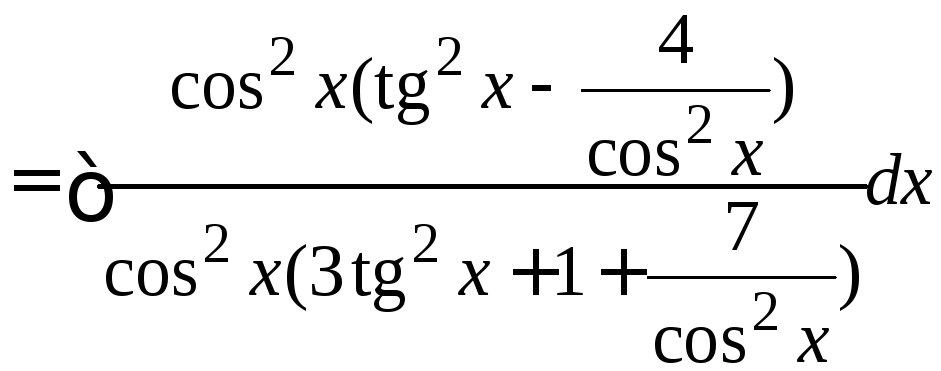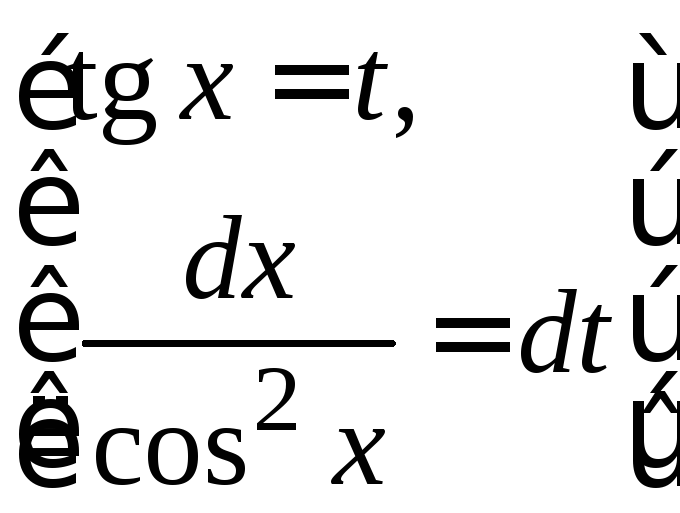
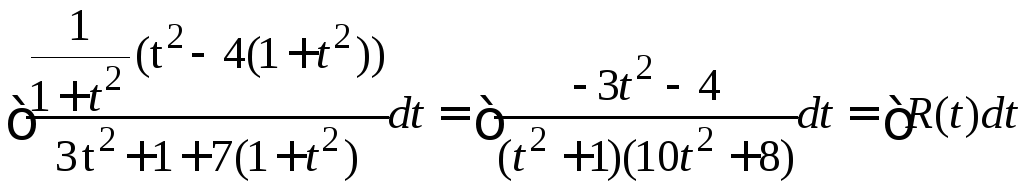г) .

;

д) . Понизим степень:.,.

Далее – возведение в степень (которая теперь вдвое меньше, чем в условии задачи) и т.д.

Примеры.

1.

= .

2.==.

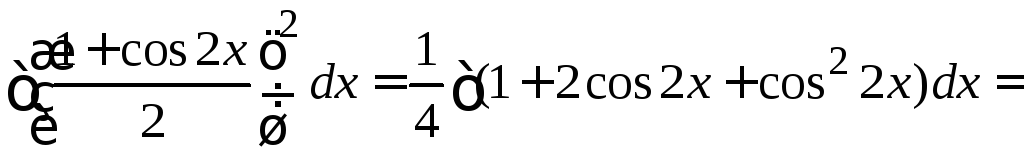е) .

Пример. .

7. Рационализирующие подстановки для интегралов от иррациональных функций: под корнями - линейная или дробно-линейная функция. (7.5.4, 7.5.5)

7.5.4. Класс ,n_i N, m_i N (i = 1, 2, …, k), дроби не сократимы.

Теорема. Функции класса интегрируемы в элементарных функциях.

Доказательство.Рационализирующей является подстановка (Nесть наименьшее общее кратное показателей корней).,

новые показатели степеней – целые.

Пример.

Проинтегрировав, подставим

7.5.5. Классы .

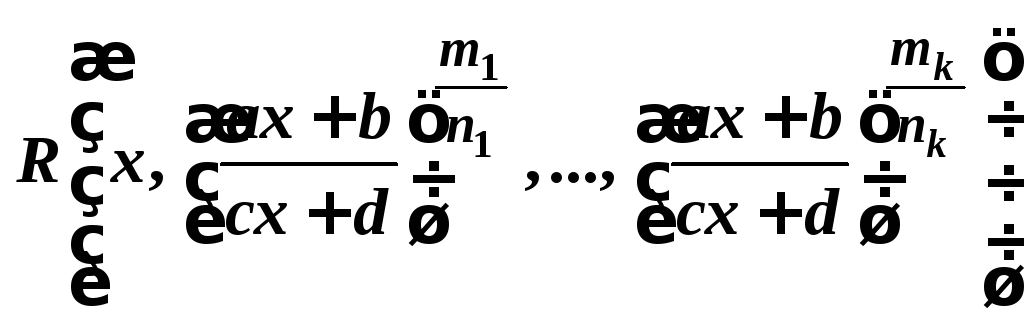Здесь n_i и m_i (i = 1, 2, …, k) натуральные, a, b, c, d – действительные.

Теорема. Каждая функция этих классов интегрируема в элементарных функциях.

Рационализирующей является подстановка.

Пример.

=

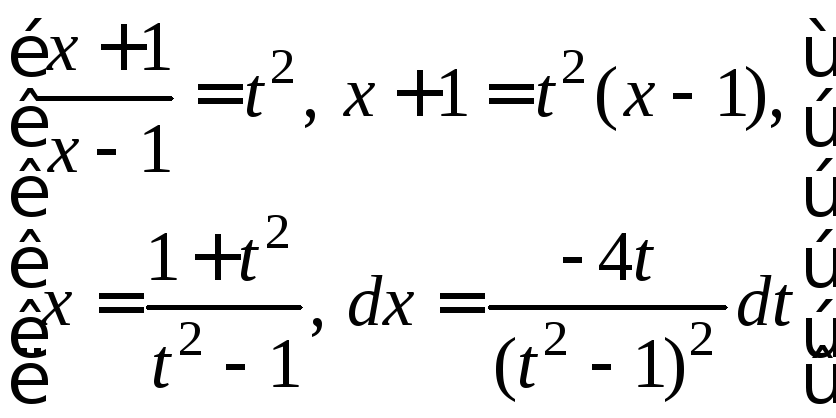
8. Подстановки для интегралов от иррациональных функций: под корнем – квадратный трехчлен. (7.5.6)

7.5.6. Класс ,a,b,cR.

Теорема.Функцииинтегрируемы в элементарных функциях.

Доказательство.

Достаточно рассмотреть функции трех следующих видов:

, a >0,так как общий случай сводится к одному из них выделением полного квадрата и введением новой переменной.

Будем использовать формулы

а)

; .

б) ;

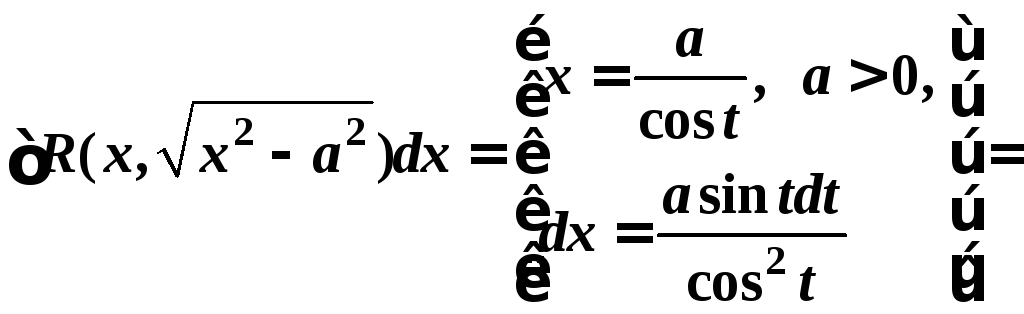
в) ;

Примеры.

1. .

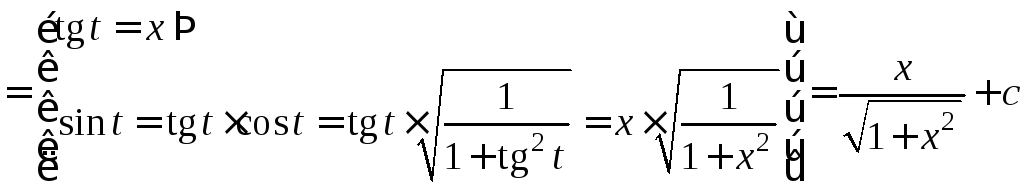2.

.

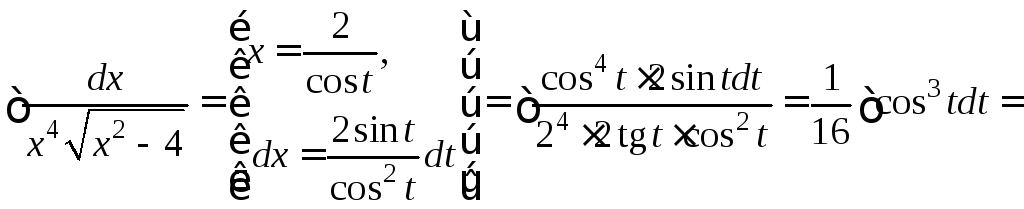
Замечание. Существуют другие рационализирующие подстановки при интегрировании функций класса . А иногда подстановки не нужны.

Приведем несколько частных случаев.

а).Интегралы виданаходятся аналогично интегралам(от рациональных дробей 3-го типа).

б)Рационализирующая подстановка:

в) Интегралы вида можно привести к одному из видов

и проинтегрировать по частям.

Пример.

.

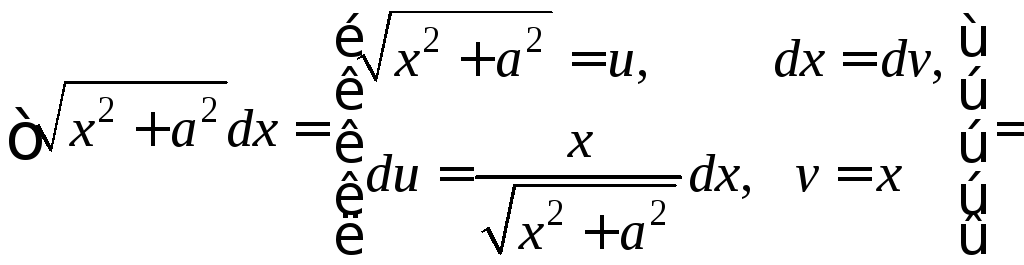
Получено уравнение, содержащее искомый интеграл  .

Аналогично;.

9.Задачи, приводящие к понятию определенного интеграла Римана. (8.1)

f: RR. Определенный интеграл Римана.

8.1. Задачи, приводящие к понятию определенного интеграла.

1. Вычисление пути s, пройденного за время Т телом, движущимся прямолинейно с переменной скоростью.

t [0, Т]; v(t) – известная зависимость скорости от времени.

Если v(t)=const: s = vТ.

Если v(t) переменная:

• разобьем отрезок времени [0, T] точками ;

• на каждом отрезке [t_i-1, t_i] (i=1, 2, , n) скорость будем считать постоянной, равной ее истинному значению v(t_i*) в некоторой точке t_i* [t_i-1, t_i].

• i 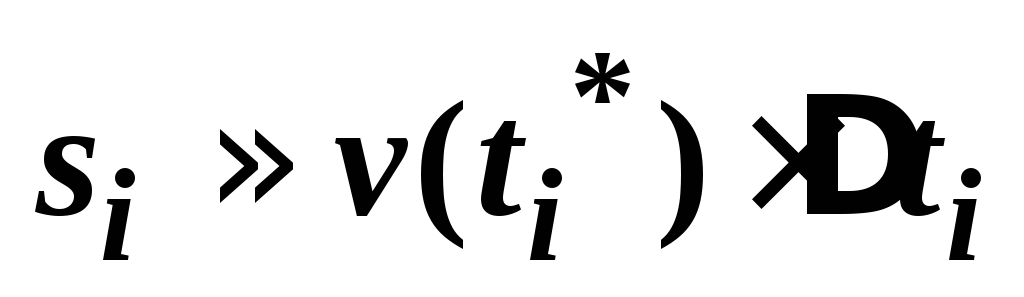– путь, пройденный за время t_i = t_i – t_i-1.

• весь путь .

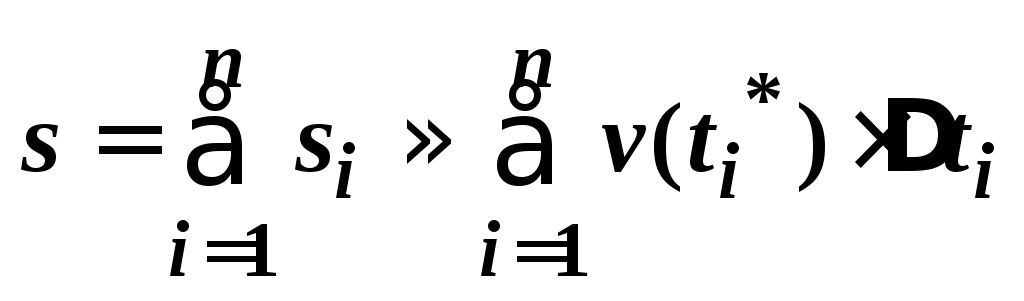Заложенная ошибка будет уменьшаться, если v(t) непрерывна, а максимальная длина отрезков [t_i-1, t_i] стремится к нулю.

2. Вычисление массы прямолинейного стержня длины l с переменной плотностью (l).

Сечение стержня считаем постоянным, с площадью 1.l[0, L], (l) = известная зависимость линейной плотности от длины.

Если (l) =const: m =  L.

Если (l) переменная:

• разобьем отрезок [0, L] точками

;

• на каждом отрезке [l_i-1, l_i] (i=1, 2, , n) плотность будем считать постоянной, равной ее истинному значению (l_i*) в некоторой точке l_i* [l_i-1, l_i].

• i 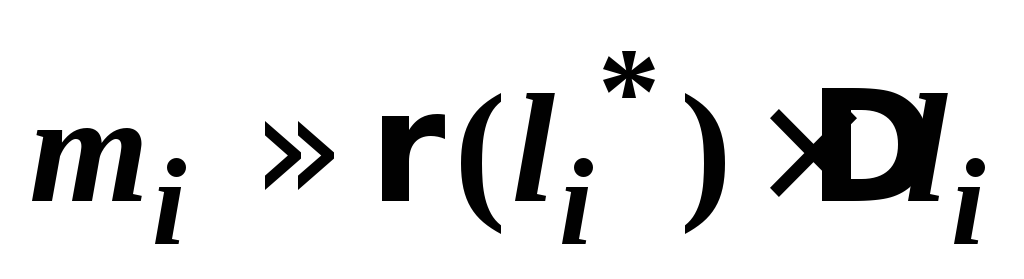– масса части стержня для l [l_i-1, l_i], .

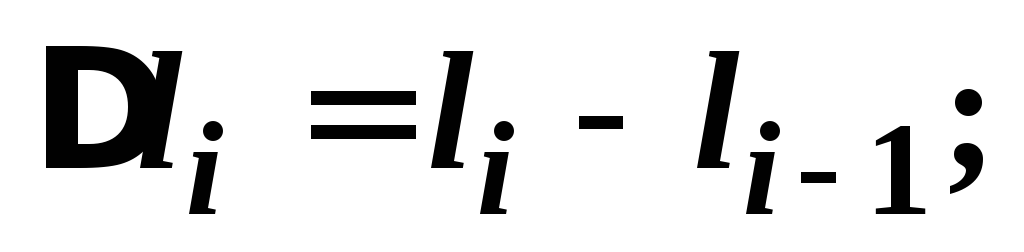• масса всего стержня

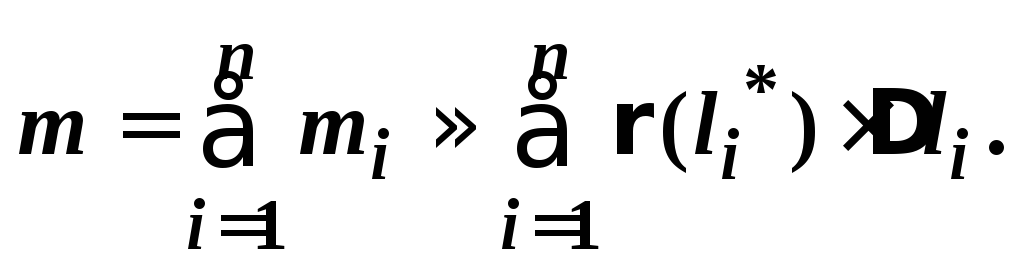
Заложенная ошибка будет уменьшаться, если (l) непрерывна, а максимальная длина отрезков [l_i-1, l_i] стремится к нулю.

3. Вычисление площади криволинейной трапеции, ограниченной сверху кривой y=f(x), снизу осью абсцисс, справа и слева прямыми x=a, x=b.

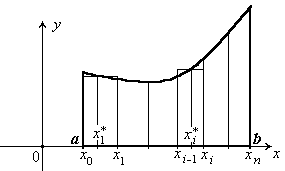Если y = h =const,S = h (b – a).

Если h = f(x) – переменная:

• разобьем отрезок [a, b]

точками ;

• на каждом отрезке [x_i-1, x_i] (i=1, 2, , n) высоту будем считать постоянной, равной ее истинному значению f(x_i*) в некоторой точке x_i* [x_i-1, x_i].

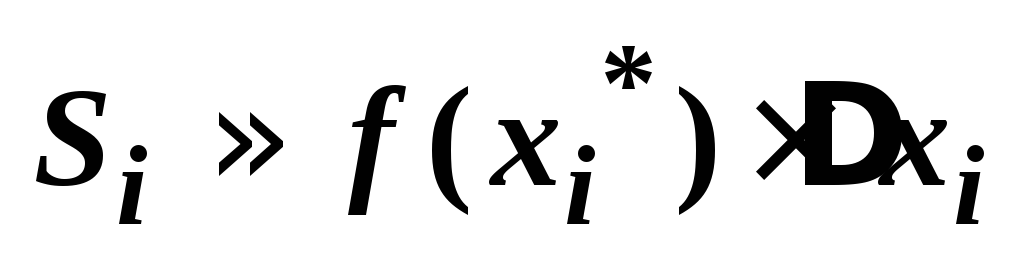• i – площадь части области при x [x_i-1, x_i], ;

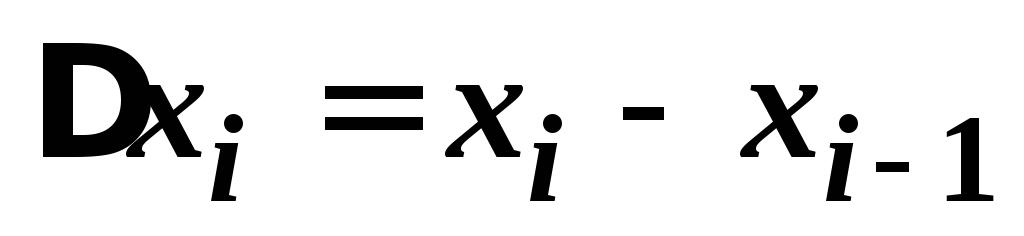• вся площадь .

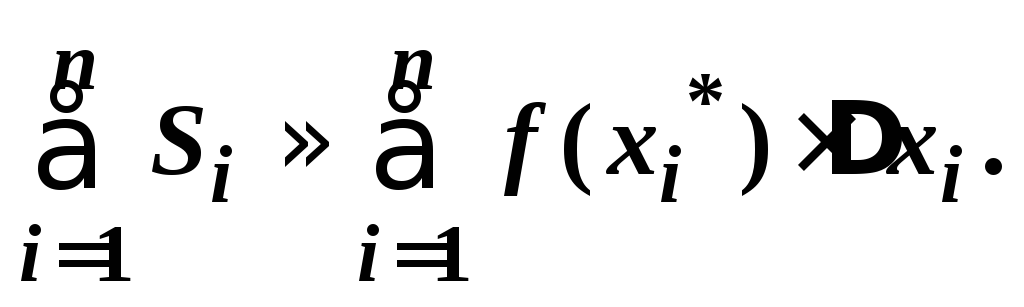Заложенная ошибка будет уменьшаться, если f(x) непрерывна, а максимальная длина отрезков [x_i-1, x_i] стремится к нулю.