Понятия первообразной и неопределенного интеграла. Существование первообразных, структура множества первообразных для функции. Свойства неопределенного интеграла. (7.1, 7.2)
7.1. Первообразные.
Определение.
Функция F(x)
называется первообразной
для
функции f(x)
на интервале (a,
b),
если x(a,
b):
.
Возникают вопросы:
когда первообразная для f(x),
сколько первообразных у f(x) и чем они различаются,
как находить первообразные.
Ответ на первый вопрос. Докажем позднее, что у непрерывных функций существуют первообразные.
Ответ на второй вопрос.
Теорема 1. Если функция f(x) имеет на (a, b) первообразную, то она имеет на (a, b) бесконечно много первообразных.
Доказательство.
F(x)
– первообразная для f(x)
сR
F(x)
+ c
– тоже первообразная для f(x),
так как
.
Теорема
2.
Пусть
и
– две первообразные для одной и той же
функцииf(x)
на (a,
b),
тогда
.
Доказательство.
,
(по
следствию теоремы Лагранжа, п. 4.1.4).
Замечание. Если первообразные определять не на интервале, теорема 2 будет не верна, что показывает следующий пример.
Пример.
на (–,
0)(0,
+).
Покажем, что F(x)
= ln
|x|
–
первообразная для f(x).
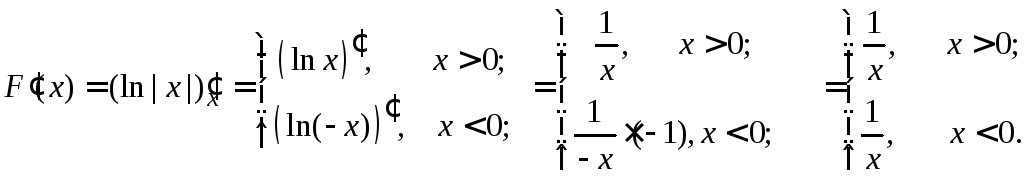
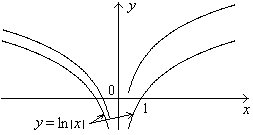сR
функция ln
|x|
+ c
– тоже первообразная для
на (–,
0)(0,
+),
но первообразными будут и функции вида
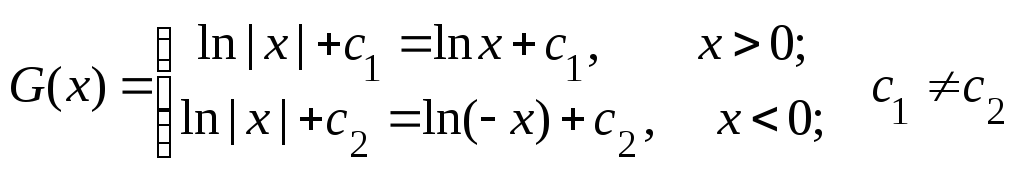
7.2. Неопределенный интеграл.
Определение. Неопределённым интегралом от функции f(x) на интервале (a, b) называется совокупность всех её первообразных на (a, b).
Обозначение:
,
f(x) – подынтегральная функция,
х – переменная интегрирования.
Из теорем пункта
7.1:
,
F(x) – одна из первообразных для f(x) на (a, b), сR.
Замечание 1. Из
определения следует:
.
Замечание 2.Под интегралом пишетсядифференциал первообразной:
f(x)dx = F (x)dx = dF(x).
Пример.
.
На (0, +)
,
на (–,
0)
.
Сокращенная запись:
.
Теорема. Основные свойства неопределённого интеграла.
1.
Линейность.
.
Доказательство. В левой части равенства бесконечно много функций, отличающихся на константу, в правой части – тоже.
Это множества первообразных для одной и той же функции.
2. Взаимная обратность операций дифференцирования и неопределенного интегрирования.
;
Пример.
,
.
3. Инвариантность интегральных формул.
(x = x(t) – функция, имеющая непрерывную производную).
Доказательство. f(x)dx = dF(x)
(по инвариантности формы дифференциала) f(x(t))dx(t) = dF(x(t))
.
Пример.
.(подчеркнем,
что
).
Замечание. Не для всех элементарных функций первообразные являются элементарными функциями. Примеры «не берущихся» интегралов:
,
,
,
,
,
.
Основные методы нахождения неопределенного интеграла. (7.4.1-7.4.3)
7.4.1. Разложение интеграла в сумму более простых интегралов (использование свойства линейности).
Примеры.
1.
2.
=
=
=
=
.
3.
.
7.4.2. Замена переменной в неопределенном интеграле (использование свойства инвариантности интегральных формул). Рассмотрим две разновидности этого метода
а) Внесение функции под знак дифференциала
Если интеграл
имеет вид
,то
запишем его так:
и
будем интегрировать по переменнойu.
Если найдем
,то
сделаем подстановкуu
=
u(x).
Примеры.
1.
=
.
2.
=
3.
4.
.
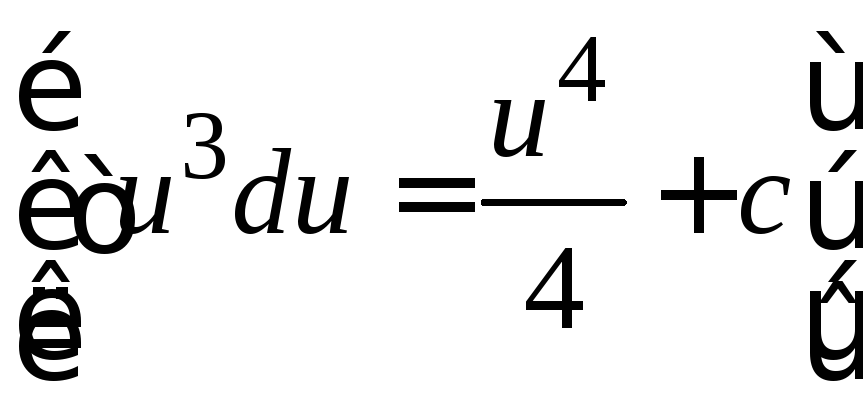
5.
=
.
6.
.
7.
=
б)
Подстановка вместо переменной
интегрирования монотонной непрерывно
дифференцируемой функции другого
аргумента и переход к интегрированию
по новой
переменной.
.
Примеры.1.
.
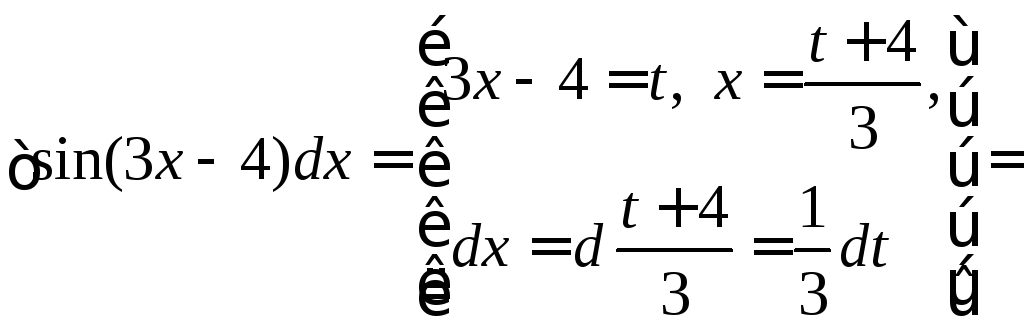
2.
.
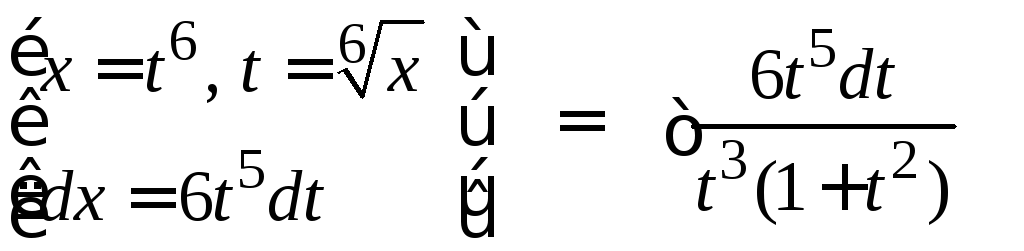
3.
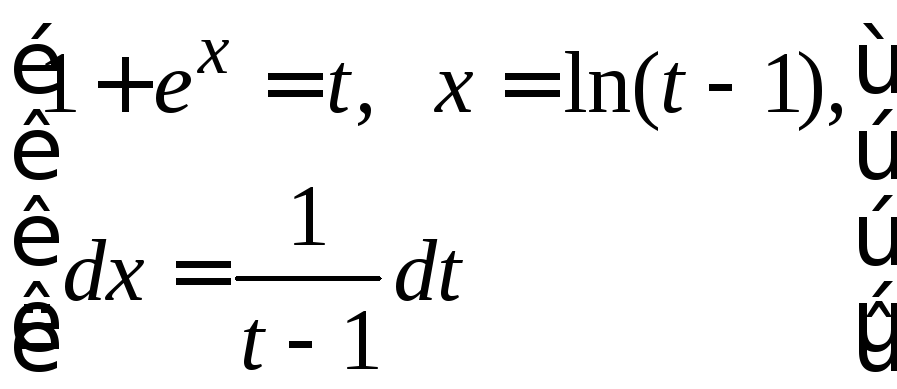
7.4.3. Интегрирование по частям (основывается на формуле производной произведения).
Пусть u(x)
иv(x)
имеют непрерывные производные. Тогда
.\
Доказательство.
.
Интегрируем:
,
,
.
Чтобы лучше понять
возможности метода, перепишем формулу
в виде
.
Один из множителей подынтегрального выраженияв новом интеграле заменен своей производной, а второй заменен своей первообразной.
Примеры.
1.
.
Функцию x можно уничтожить дифференцированием.
=
=
.
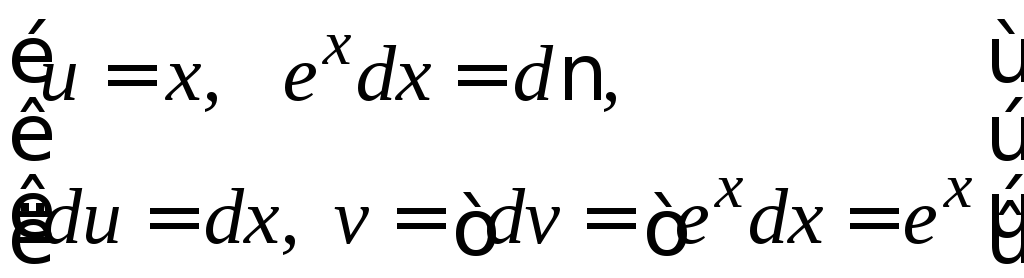Замечание.
Неверный
выбор u
и dv
может завести в тупик. Например, если
в
взять
(тогда
),
придем к равенству
,говорящему
о бессмысленности выполненных действий.
2.
(
=
=
.
3.
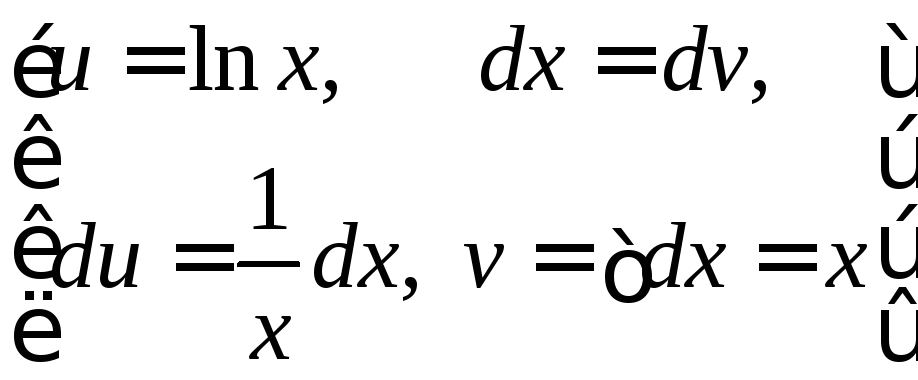
4.
=
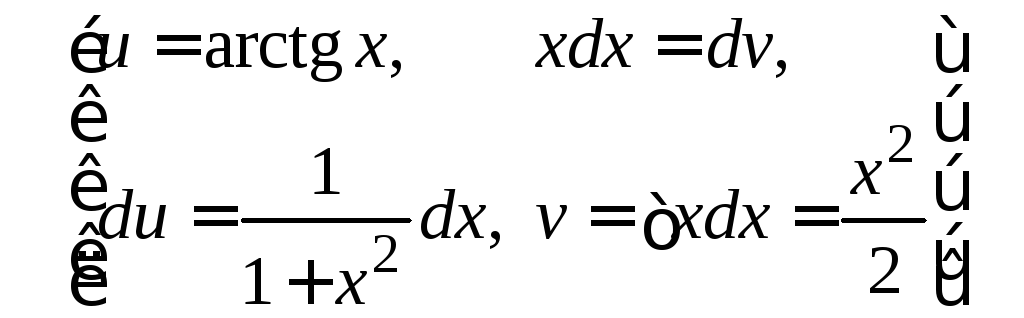5. Пример «циклического» интеграла: после двух применений формулы метода интегрирования по частям интеграл находится решением полученного уравнения.
=
.
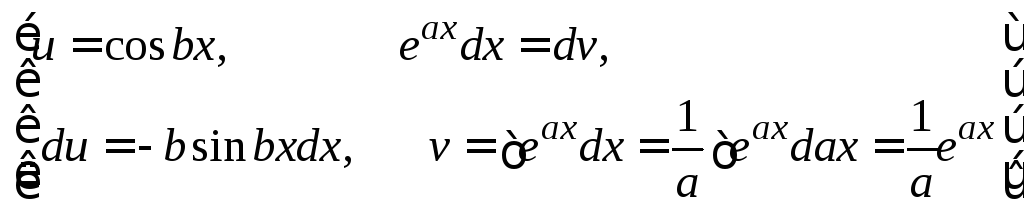
Получено уравнение, содержащее искомый интеграл:
.
.Окончательно,
.
Аналогично
.
Интегрирование рациональных функций. (7.5.1)