12. Инвариантность формы дифференциала. Формулы частных производных сложных функций.(6.2.9)

6.2.9. Свойства дифференциала. Частные производные сложной функции.

Теорема 1. Алгебраические свойства дифференциала.

Пусть u(x₁, x₂, …, x_n) и v(x₁, x₂, …, x_n) дифференцируемы, c = const.

1. d(cu) = cdu;

2. d(u  v) = du  dv;

3. d(uv) = udv + vdu;

4.

Доказательство (n = 2).

Дифференциалы представим как суммы частных дифференциалов функций одной переменной, свойства которых известны.

Свойство 3:

Теорема 2. Инвариантность формы дифференциала. Дифференциал сложной функции может быть получен с помощью подстановок из дифференциалов составляющих ее функций.

Справедливость теоремы следует из представления дифференциала функции нескольких переменных в виде суммы дифференциалов функций одной переменной, которые обладают инвариантностью формы.

Несколько частных случаев (все функции дифференцируемы).

1. Пусть

z= z₁(u,v) ( будем писатьz(u,v)). .

Подставим дифференциалы dx,dy:=

.

Из единственности дифференциала 

или

2. .

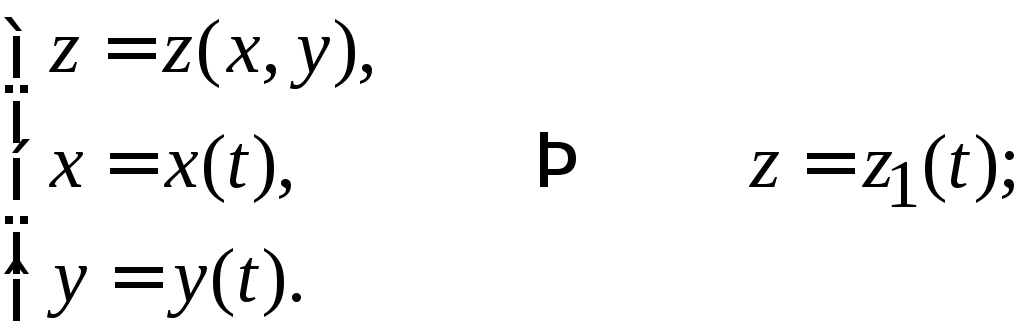
3. .

Пример. ,



.



13. Инвариантность формы дифференциала. Формулы частных производных неявных функций. (6.2.10)

6.2.10. Теорема существования неявной функции. Производная (частные производные) неявной функции.

Теорема 1. Пусть (x₀, y₀) – одно из решений уравнения F(x, y) = 0.

Если F(x, y) дифференцируема в окрестности т.(x₀, y₀), F_y (x, y) непрерывна и F_y (x₀, y₀)  0, то в некоторой U_(x₀)(–; )  дифференцируемая функция y(x), которая при подстановке в уравнение превращает его в тождество и y(x₀) = y₀.

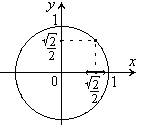Примеры.

1. x² + y² = 1. F(x, y) = 0, F(x, y) = x² + y² –1.

Точка (x₀, y₀) = – одно из решений.

F_y (x, y) = 2y в т.(x₀, y₀) непрерывна и  0.

Изображена окрестность т. x₀ =, в которой  дифференцируемая неявная функция, задаваемая уравнением, ее график проходит через т. (x₀, y₀).

2. x² + y² = 1, (x₀, y₀) = (1, 0) – решение.

F_y (x, y) = 2y непрерывна,

но = 0 в т. (x₀, y₀).

Точка x₀ = 1 не имеет окрестности,

в которой  неявная функция, заданная уравнением.

3. (x₀, y₀) = (0, 1) – решение.

F(x, y) =  F(x, y) = 0.

F_y (x, y) = в т. (x₀, y₀) непрерывна и  0.

Но F(x, y) в этой точке не дифференцируема, так как F_x (x, y) = в точке (0, 1) не .

В окрестности т. x₀ = 0 определена неявная функция, задаваемая уравнением, такая, что y(x₀) = y₀, однако она не является дифференцируемой.

Теорема 2. Пусть (x₀, y₀, z₀) – одно из решений уравнения F(x, y, z) = 0.

Если F(x, y, z) дифференцируема в окрестности точки (x₀, y₀, z₀),F_z (x, y, z) непрерывна и F_z (x₀, y₀, z₀)  0, то в некоторой окрестности т. (x₀, y₀) на плоскости  дифференцируемая функция z(x, y), которая при подстановке в уравнение превращает его в тождество и z (x₀, y₀) = z ₀.

Методы нахождения производной (частных производных) неявной функции.

1. y(x) задана уравнением F(x, y) = 0.

Метод первый (уже знаком нам):( F(x, y(x)) )_x = 0.

Метод второй. F(x, y) = 0, y = y(x). Имеем сложную функцию.

. Но (*)

Метод третий. F(x, y) = 0, y = y(x).

Используем свойство инвариантности формы дифференциала.

1. (x, y) – независимые переменные:.

2. y = y(x)  F(x, y(x))  0  снова(*)

Пример. По формуле (*) .

2. z(x, y) задана уравнением F(x, y, z) = 0. Используем третий метод как самый короткий.

1) ,

2) z = z(x, y)  dF  0:

.

В силу единственности дифференциала:,получаем(**) или, в других обозначениях,,. (**)

Пример. z ³ – 3xyz = 8. F(x, y, z) = z ³ – 3xyz – 8,

По формуле (**)

Замечание. Производная (частные производные) неявной функции выражаются не только через независимые переменные, но и через саму неявную функцию.