8. Предел функции двух переменных. Связь двойного предела с повторными. (6.1.1)

6.1.1. Предел функции нескольких переменных. Повторные пределы.

f: RⁿR задана в некоторой окрестности точки M₀, кроме, может быть, самой точки M₀.

Определение. Число А называется пределом функции

f(x₁, x₂, …, x_n) в точке M₀, если

>0 >0 M ( 0 < (М₀, М) <   | f (M) – A|<  ).

Формы записи:

n = 2:

Это двойной предел.

На языке окрестностей точек: >0 >0 M(x, y) (M U_(M₀)\M₀  f (x, y) U_(А) ).

(M может приближаться к М₀ по любому пути).

Повторные пределы:

и .

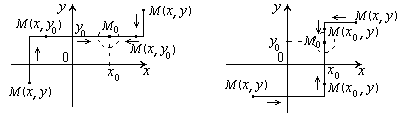
(M приближается к М₀ соответственно по горизонтали и по вертикали).

Теорема о связи двойного и повторных пределов.

Если  двойной предел и пределы ,,

то  повторные пределы ,и равны двойному.

Замечание 1. Обратное утверждение не верно.

Пример. f (x, y) =

,.

Однако двойной предел =

не существует, так как в любой окрестности точки (0, 0) функция принимает и «далекие » от нуля значения, например, если x = y, то f (x, y) = 0,5.

Замечание 2. Даже если  АR: f (x, y)  А

при движении M к M₀ по любой прямой, двойной предел может не существовать.

Пример. f (x, y) = ,M₀ (0, 0). M (x, y)  M₀ (0, 0)

4. вдоль осей x = 0 или y = 0 f (x, y) = 0 .

5. y = kx, k  0 

6. y = x², 

Вывод: предел (двойной) не существует.

Пример нахождения предела.

f (x, y) = , M₀ (0, 0).

Покажем, что число 0 есть предел функции в точке M₀.

= ,

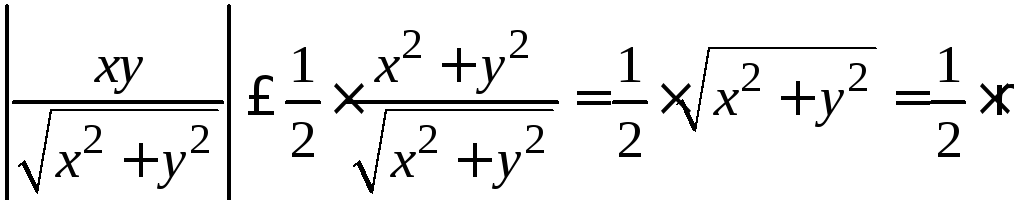 – расстояние между точками М и M₀.( воспользовались неравенством ,

которое следует из неравенств )

Зададим  > 0 и пусть  = 2.  <  

9.Определение частной производной. Частные производные высших порядков. Теорема о смешанных производных. (6.2.3, 6.3.1)

6.2.3. Частные производные.

Определение. Зафиксируем значения всех переменных, кроме одной  f (x₁, x₂, …, x_n) становится функцией одной переменной. Если полученная функция имеет производную, эта производная называется частной производной функции f (x₁, x₂, …, x_n) по соответствующей переменной.

n = 2, f(x, y).

Фиксируем y = y₀. f(x, y₀).

Частная производная по x:

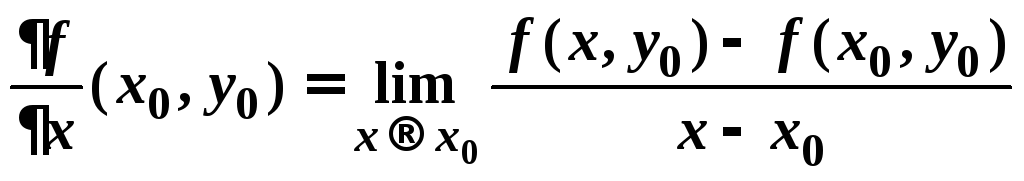или

В числителе – частное приращение функции f(x, y)

в т. (x₀, y₀) по переменной x.

Аналогично

Замечание 1. Символы , должны рассматриваться как целое, числитель и знаменатель не имеют отдельного смысла

(в отличие от символа в случае функции одной переменной, обозначающего отношение дифференциала функции к дифференциалу (приращению) независимой переменной).

Замечание 2. Могут использоваться другие обозначения частных производных, например,

.

Пример. , т.M₀(1,1).

1 способ. Подставим y =1: , т.M₀(1,1).

.

2 способ. При нахождении частной производной вторую переменную фиксируем на произвольном значении

(с переменной обращаемся как с константой)

и только затем подставим заданные значения.

, т. M₀(1,1).

,.

6.3.1. Частные производные высших порядков.

Функция – частные производные первого порядка.

Частные производные второго порядка:

.

Производная приk  i называется смешанной.

Другие обозначения: _.Частными производными порядка m от функции называются частные производные 1-го порядка от любых ее частных производных порядка m – 1.

Пример. .

,

,

(одно дифференцирование по y и два по x):.

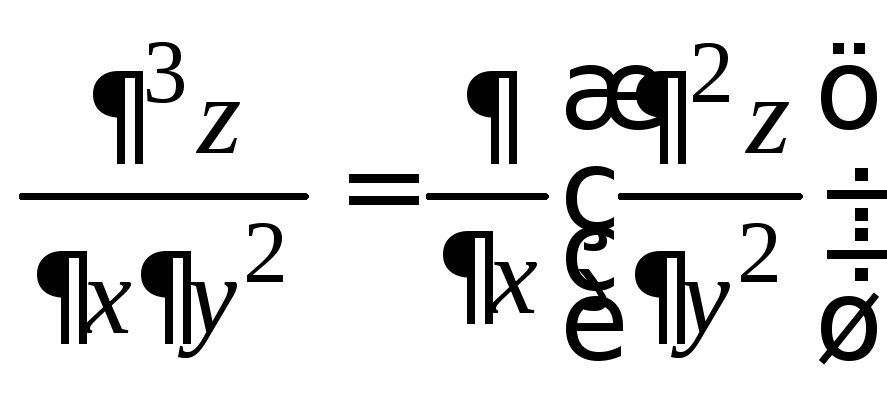
(одно дифференцирование по x и два по y): 36x²y².