5. Производная и дифференциал векторной функции, геометрическая интерпретация.Уравнения касательной к кривой в пространстве. (5.3)

5.3. Производная и дифференциал векторной функции.

5.3.1. Определение и геометрическая интерпретация производной векторной функции.

Понятие производной вводится, как и в случае

f: R  R для характеристики мгновенного изменения функции.

Определение.

.

Определим направление производной :

Вектор направлен по секущей, поэтому вектортакже направлен по секущей,

причем всегда в направлении движения, соответствующем возрастанию параметра t.

Вывод: вектор направлен по касательной к траектории в сторону движения точки при возрастании параметра t.

Теорема. .  .

При этом .

Доказательство.

=

Следствие. В декартовой системе координат =

5.3.2. Дифференциал векторной функции.

Обозначим

,

, – приимеет первый порядок относительноt.

Главную часть приращения, линейную относительно t назовем дифференциалом: ,

функцию – дифференцируемой: .

При  0 и t  0 выполняются соотношения ,

Очевидно, дифференцируемая функция непрерывна.

5.3.3. Правила дифференцирования.

Теорема. Пусть ,,– дифференцируемые векторные функции,f(t) – дифференцируемая скалярная функция, R. Тогда

1. .

2. =.

3. = .

4. = .

5. =.

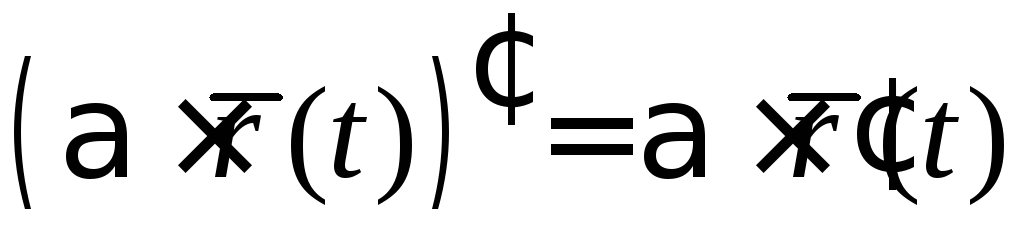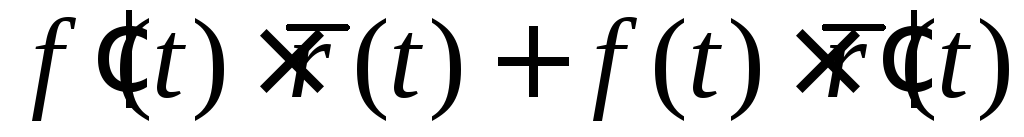Пример. = – производная скалярного квадрата.

Докажем 3:

=

= .

Докажем 5:

=

(в числителе добавим и вычтем слагаемое )

=

=.

Использовались свойства предела суммы и произведения, а также непрерывность дифференцируемой функции .

5.3.4. Уравнения касательной к кривой в трехмерном пространстве.

Кривая

Рассмотрим векторную функцию –радиус-вектор движущейся точкиM(t) L.

Вектор

может быть использован в качестве направляющего вектора касательной к кривой в точке для составленияканонических уравнений касательной:

.

Пример. L: _,

Составить уравнение

касательной.М().

.

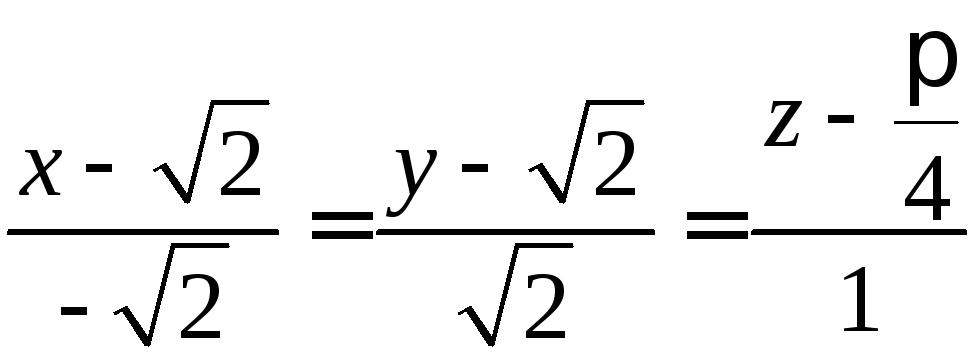6. Определение декартова произведения множеств. Определение функции нескольких переменных. График. Линии и поверхности уровней. (1.2, 6, 6.2.8)

АB – декартово произведение множеств – множество, содержащее все возможные упорядоченные пары (a, b) элементов aА и bB.

Примеры.

–декартов квадрат множества действительных чисел – состоит из упорядоченных пар (x; y) действительных чисел и изображается точками плоскости с декартовой системой координат.

состоит из упорядоченных троек действительных чисел (x; y; z) и изображается точками трехмерного пространства.

–декартова n-ая степень множества R – это множество всех упорядоченных наборов (строк) из n действительных чисел; один элемент (точка) M множества есть строка(x₁, x₂, …, x_n).

6. F: Rnr – действительные функции нескольких (многих) действительных переменных.

D(f)Rⁿ (пространстве строк длины n из действительных чисел).

Заметим, что Rⁿ не является упорядоченным множеством, но является линейным пространством.

М  Rⁿ  М = (x₁, x₂, …, x_n)  М(x₁, x₂, …, x_n);

f(M) = f(x₁, x₂, …, x_n)  R.

n = 2  f(x, y);

n =3  f(x, y, z).

Дляf: R²R возможно построение графика – поверхности в трехмерном пространстве, состоящей из точек (x, y, f(x, y)).

Примеры.

1. u = x²yz; область определения D(u) = R³.

2. ; D(u) = R³ \ (плоскость z= 0).

3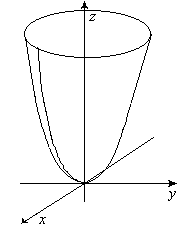. ;D(z) определяется неравенством xy > 0.

4. z = x² + y², D(z) = R²,

график – параболоид вращения.

6.2.8. Градиент. Линии или поверхности уровней.

Определение. Градиентом непрерывно дифференцируемой функции f(x₁, x₂, …, x_n) в т. М(x₁, x₂, …, x_n) называется вектор

f(M) = grad f(M) =

n = 3, f(x, y, z) 

Теорема.

Доказательство. По определению

Это скалярное произведение векторов

f(M) = и ⁰= {cos, cos, cos}.

Следствие (механический смысл градиента). Пусть f(M)  0. Производная максимальна, когда направление вектора совпадает с направлением градиента функции. Величина ее в этом случае равна

Таким образом, градиент задает максимальную для данной точки скорость роста функции как по величине, так и по направлению.

Определение. Линия на плоскости, определяемая уравнением f(x, y) = с, где f(x, y) непрерывна, а с = const,

называется линией уровня с функции f(x, y).

Поверхность в трехмерном пространстве, определяемая уравнением f(x,y,z) = с, где f(x,y,z) непрерывна, а с = const, называется поверхностью уровня с функции f(x, y, z).

Другими словами, линия уровня функции – это геометрическое место точек в ее области определения, в которых она принимает одно и то же значение. Через каждую точку области определения функции проходит линия уровня, линии различных уровней не пересекаются.

Аналогично для поверхностей уровня.

Теорема. Пусть f непрерывно дифференцируема и grad f(M₀)  0. Вектор grad f (M₀) перпендикулярен поверхности (линии) уровня функции f, проходящей через т. М₀.

Доказательство. Пусть S – поверхность f(x, y, z) = с. М₀  S, М  S, М  М₀ по поверхности.

Тогда f (М₀)|_МS = f(M) – f(M₀) = 0, т.е.

df (М₀) )|_МS + o() = 0,

df (М₀) )|_МS = – o(),

где  = (М, М₀) – расстояние между точками.

Пусть  – угол между градиентом и вектором (между градиентом и отрезком, секущим поверхность).

( |f(M₀)|cos )|_МS = – o(),

т. е.Но это возможно только если ,

т. е. (угол между градиентом и касательным направлением к поверхности)._.

Выбирая путь приближения МкМ₀, мы можем получить в пределе любое направление, касательное к поверхностиS.Градиент перпендикулярен касательной плоскости, проходящей через т. М₀.

Следствие. для любого направления, касательного к проходящей через точку Мповерхности (линии) уровня функцииf.

Примеры.

1.z = x²+y².

Область определения: вся плоскость (x, y).

z = 0  x² + y² = 0 – линия нулевого уровня вырождается в точку;

z = с > 0  x² + y² = c – линия уровня c есть окружность радиуса с центром в точке (0, 0).

z(x, y) = {2x, 2y} – направление градиента совпадает с направлением радиус-вектора точки.

2. z = 3x – y.

Область определения: вся плоскость (x, y).

Линии уровней z = c представляют из себя параллельные прямые y = 3x – c;

градиент есть постоянный вектор: z(x, y) = {3, –1}.

3. .

Область определения: вся плоскость (x, y).

z = 0  xy = 0  (x = 0  y = 0).

Линия нулевого уровня – пара пересекающихся прямых (оси координат).

z = с  0  xy = 2c  .

Линии уровней есть гиперболы.

Градиент z(x, y) = .

4. u = x² + y² + z².

Область определения: все пространство (x, y, z).

Поверхностями уровней с > 0 являются концентрические сферы x² + y² + z² = с.

u(x, y, z) = {2x, 2y, 2z}, направление градиента совпадает с направлением радиус-вектора точки, т.е. перпендикулярно поверхности проходящей через эту точку сферы.

7. Предел функции двух переменных. Непрерывность. Множество значений непрерывной функции на замкнутом ограниченном множестве. (6.1.1, 6.1.2, 6.1.3)