2.2. Сложная функция.
Пусть заданы две функции: f: D(f) E(f), g: D(g) E(g).
Если E(f) D(g), то на D(f) определена сложная функция (композиция, суперпозиция)
,
.
Пример. y = sin x, z = y2 z = sin2 x.
Замечание.
В общем случае
.
Пример. f(х) = sinx, g(х) = x2, то
=
sin
x2,
= sin2
x.
2.5.13. Предел сложной функции. Замена переменной при вычислении предела.
Теорема. Пусть в окрестности точки x0 (возможно, кроме самой x0) определена сложная функция
и пусть
и
,
причем f(x) y0 при x x0
.
Доказательство. Зададим >0.
Найдем 1 > 0: y (0<|y – y0|< 1 | g (y) – z0|< ).
Найдем >0:
x (0<|x – x0|< |f (x) – y0| < 1).
В итоге для заданного >0 найдено >0 такое, что
x (0<|x – x0|<
(| g(f(x)) – z0| = | g(y) – z0| <).
Следствие. Из теоремы следует формула замены переменной:
Примеры.
1.
.
2.
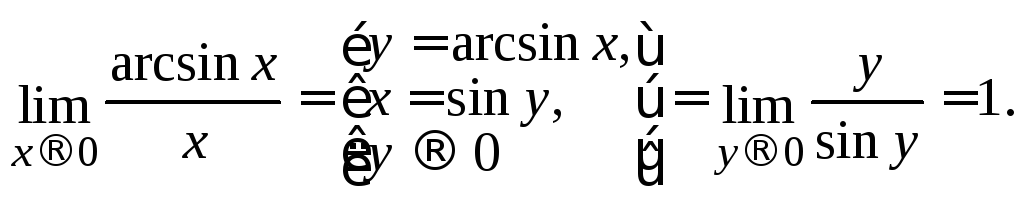
3.
Если (x)
– б.м. в точке x0,
т. е. если
и если (x) 0 при x x0 в некоторой U(x0),
то
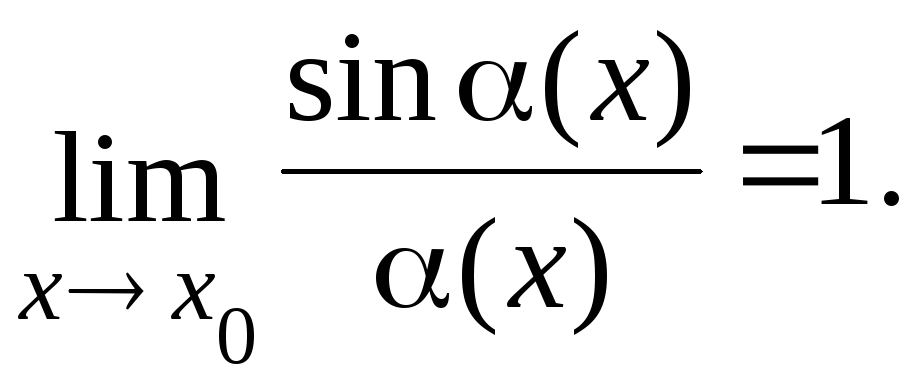
7.Определение непрерывной функции, различные формы записи. Свойства функций, непрерывных в точке. Элементарные функции. Предел показательно-степенной функции, возникающие неопределенности. (2.1, 2.4, 2.5.2, 2.5.14, 2.5.16, 2.5.17)
Запишем определение непрерывности функции из R в R
с использованием конкретной метрики.
Определение. Функция f: RR называется непрерывной в точке x0, если x0 принадлежит области определения D(f) вместе с некоторой своей окрестностью и
>0 >0 x (|x – x0|< | f (x) – f (x0)|< ).
Или, на языке окрестностей точек:
>0 >0 : f(U(x0)) U(f(x0)).
Замечание. Графиком непрерывной функции f: RR является непрерывная кривая в плоскости (x, y).
Среди других свойств функций f: RR выделим четность, нечетность и периодичность. Повторить самостоятельно.
Сведем вместе все формы записи определения непрерывности функции в точке.
Определение. Функция f: RR называется непрерывной в точке x0, если x0 принадлежит области определения D(f) вместе с некоторой своей окрестностью и верно одно из утверждений:
(1) >0 >0 x ( |x – x0|< | f(x) – f(x0)|< )
или
(2)
или
(3)
или
(4)
или
(5)
или
(6) >0 >0 x ( x U(x0) f(x) U(f(x0)) ).
2.5.16. Свойства функций, непрерывных в точке.
Теорема 1. Сохранение знака.
Если f(x) непрерывна в т. x0 и f(x0) 0, то в некоторой U(x0) f(x) имеет тот же знак, что и f(x0).
Если f(x) непрерывна в т. x0 и сохраняет знак на
U (x0)\{x0}, то f(x0) имеет тот же знак или f(x0) = 0.
Теорема 2. Алгебраические свойства. Пусть f(x) и g(x) непрерывны в т. x0 и сR.
Тогда в т. x0 непрерывны функции f(x) g(x), с∙f(x),
f(x)g(x);
при g(x0)
0.
Докажем, например, что произведение непрерывных функций есть непрерывная функция.
Теорема 3. Непрерывность сложной функции.
Пусть в окрестности
точки x0
определена сложная функция
.
Если f(x)
непрерывна в точке x0,
g(y)
непрерывна в точке
то
непрерывна в точке
x0.
Доказательство. Зададим >0.
Найдем 1 > 0:
Найдем >0:
для заданного >0 найдено >0:
Теорема 4. Непрерывность обратной функции.
Если f(x)
непрерывна в точке x0
и взаимно
однозначна в некоторой ее окрестности,
то обратная функция
непрерывна в точке
.
Доказательство. Зададим >0. Нужно найти >0 такое, что
y (0 < |y – y0| < | f–1 (y) – f–1 (y0)| < ).
Последнее неравенство означает: | f–1 (y) – x0|< .
Непрерывная взаимнооднозначная функция монотонна.
Рассмотрим U(x0). Ее образом будет некоторый интервал (c; d) оси Oy, содержащий точку y0.
Возьмем U(y0) (c; d).
y U(y0) | f–1 (y) – x0|< .