2.5.10. Неопределенности.
Алгебраические свойства предела допускают обобщение на функции, являющиеся б. м. или б. б. в точке х0. Например (здесь с 0):
Но должны быть исключены случаи так называемых неопределенностей:
,
когда применение алгебраических свойств не имеет смысла: заранее не известен результат.
Примеры.
Пусть
Тогда
.
Вычислим предел
суммы:
(Вместо могло быть любое число. А если
2 заменить на
получится
бесконечно большая).
Пусть
Вычислим предел
произведения:
Пусть
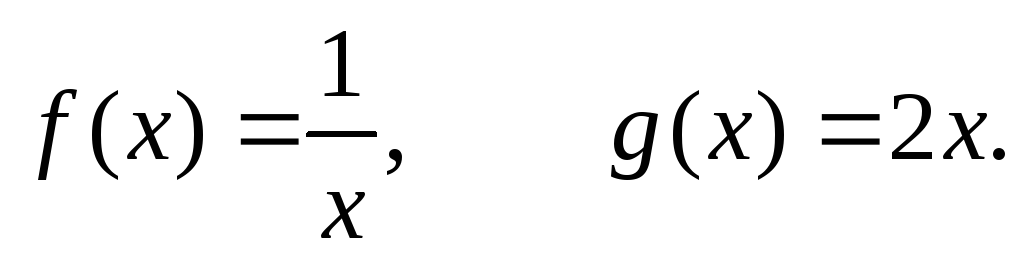
Вычислим предел
произведения:
Замечания.
1.
Если
не существуют,
то пределы
,
,
могут
и существовать.
2.
Если существует
только один
из пределов:
а
второй
не существует,
то
не
существует,
может
существовать
при А
= 0.
Пока у нас есть один способ избавления от неопределенности – тождественные преобразования функции
(на основании теоремы о единственности предела), например, сокращение одинаковых множителей в числителе и знаменателе дроби. В дальнейшем наши возможности в борьбе с неопределенностями расширятся.
5.Односторонние пределы функции в точке. I замечательный предел. (2.5.1, 2.5.11, 2.5.12)
2.5.11. Односторонние пределы.
Иногда
ищется при условии x
> x0
(предел
справа, правосторонний предел)
или при условии x < x0 (предел слева, левосторонний предел).
В этих случаях вместо окрестности точки x0 рассматривается полуокрестность (правая или левая).
,
.
Пример.
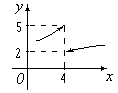
В дальнейшем будем также использовать следующие обозначения:
,
Теорема. Предел функции в точке односторонние пределы и равны между собой.
Доказательство следует из определений (две полуокрестности точки x0 определяют окрестность, о которой идет речь в определении предела).
Замечание. Для односторонних пределов могут быть переформулированы все свойства и теоремы, сформулированные для обычного (двустороннего) предела.
2.5. Предел функции в точке.
2.5.1.
Пример.
Рассмотрим функцию
D(f) = (– , 0) (0, ). Это четная функция.
x
> 0
: –
1
sin x
1
график расположен между графиками двух гипербол.
Что будет при x 0?
Оказывается, что значения функции f(х) при стремлении x к нулю неограниченно приближаются к единице, хотя и никогда ей не равны. При этом точность приближения мы можем задавать сами:
>0 >0 x (0< |x|< |f(x) – 1|<).
Здесь зависит от : чем точнее мы хотим приблизиться к 1, тем ближе мы должны подойти к точке x = 0.
Коротко
происходящее записывается так:
Это первый замечательный предел (позднее мы докажем его).
2.5.12. Доказательство первого замечательного предела
В
следствие
четности функции
достаточно рассматривать предел справа.
Пусть x > 0. Переобозначим
x = .
Из рисунка:
.
То
есть:
.
Умножим
на 2 и разделим на sin
0:
или
Теперь
,
> 0.
.
По
лемме о двух милиционерах делаем вывод
о существовании предела
Из
четности функции
6.Понятие сложной функции. Предел сложной функции. Замена переменной при вычислении пределов. (2.2, 2.5.13)