21. Дифференциалы высших порядков. Формула Тейлора. Приближенные вычисления с заданной точностью (3.15.2, 4.3.2, 4.4.3)
3.15.2. Дифференциалы высших порядков.
df (x) = f (x)dx – линейная функция от dx = x
с коэффициентом f (x). Это дифференциал (первый дифференциал).
Первый дифференциал дает линейное приближение приращения функции (с точностью до слагаемого,
«о-малого» по сравнению с x).
Пусть у функции f (x) в точке x существуют производные более высоких порядков.
Второй дифференциал, дифференциал второго порядка:
d2 f (x) = f (x) (dx)2 – квадратичная функция от dx = x.
Скобки на dx принято опускать:
d2 f (x) = f (x) dx2.
Третий дифференциал функции f(x) в точке x:
d3 f (x) = f (x)(dx)3 – кубическая функция от dx = x.
d3 f (x) = f (x)dx3.
Дифференциал n-го порядка функции f(x) в точке x: степенная функция от x
dn f (x) = f (n) (x)(dx)n.
Принятая форма записи:
dn f (x) = f (n)(x)dxn.
Замечание 1. Далее мы увидим, что с помощью дифференциалов высших порядков можно в окрестности рассматриваемой точки приблизить приращение функции с точностью до слагаемого, «о-малого» по сравнению
с (x)n.
Замечание 2. На основании определений дифференциалов применяются следующие обозначения производных:
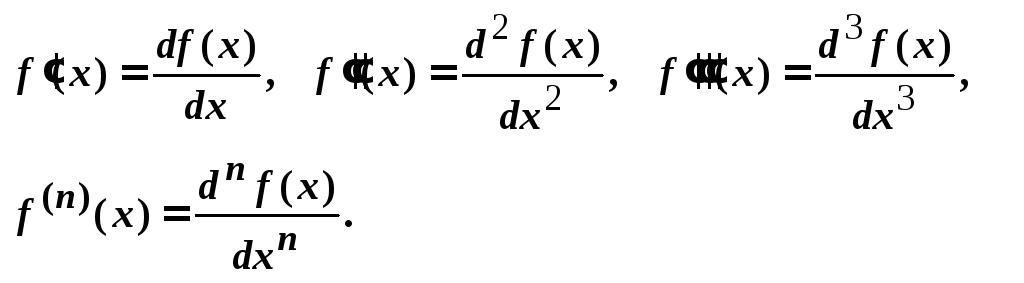
Замечание 3. Дифференциалы высших порядков инвариантностью формы не обладают.
В выражения, их содержащие, нельзя делать функциональные подстановки.
Пример. f (x) = x2, x(t) = t2.
Образуем сложную функцию: f (x(t)) = t4.
Ее первый и второй дифференциалы равны
d(f (x(t))) = 4t3dt и d2(f (x(t))) = 12t2dt2.
Если же мы попытаемся получить эти дифференциалы подстановкой дифференциалов функции x(t)
dx(t) = 2tdt и d2x(t) = 2dt2
в дифференциалы df (x) = 2xdx и d2 f (x) = 2dx2,
то получим:
d(f (x(t))) = 2t2 2tdt = 4t3dt и
d2(f (x(t))) =2(2tdt)2= 8t2dt2.
Второй результат не верен.
Для первого же дифференциала мы получили одинаковые результаты: первый дифференциал обладает инвариантностью формы.
Замечание 4. Предостерегаем от ошибок следующего рода.
Одна и та же запись dx2 может означать
dx2 = (dx)2 и dx2 = d(x2) = 2x dx.
Конкретное содержание определяется контекстом, смыслом формулы.
4.3.1. Формула Тейлора для многочлена. Запишем многочлен по возрастанию степеней его слагаемых:
Многочлен записан по степеням x. Если он изучается в окрестности точки x0, то его удобнее записать по степеням
(x – x0).
Подставим x = (x – x0) + x0 и приведем подобные:
Pn (x) = a0 + a1(x – x0) + a2(x – x0)2 + … + ak(x – x0)k +
+ … + an(x – x0)n.
Выведем формулы для новых коэффициентов.
a0 = Pn (x0).
Pn (x) = a1 + 2a2(x – x0) + 3a3(x – x0)2 + …+ kak(x – x0)k–1 + …+ nan(x – x0)n–1,
a1 = Pn (x0);
Pn (x) = 2a2 + 32a3(x – x0) +…+ k(k–1)ak(x – x0)k–2 +
…+ n(n–1) an(x – x0)n–2,
Pn(k)(x) = k!ak + … + n(n–1)…(n – k +1) an(x – x0)n–k,
Итак
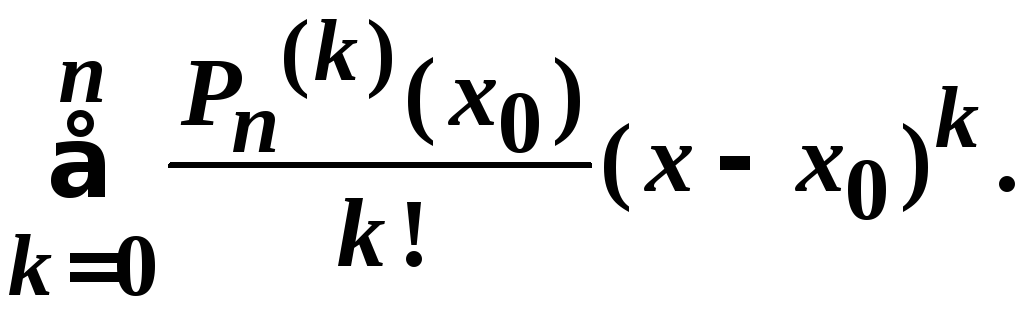
Это формула Тейлора для многочлена в окрестности точки x0 ( по степеням (x– x0) ).
0! = 1.
Разложение многочлена по степеням (x – x0) единственно, т. к. коэффициенты определяются однозначно (по полученным формулам).
Пример. Разложить многочлен P5(x) = P(x) = x5 – 2x по степеням (x + 1).
Здесь x0 = –1. Найдем коэффициенты формулы Тейлора.
a0 = P (–1) = (–1)5 – 2(–1) = 1,
a1 = P (–1) / 1! a1 = (5x4 – 2)|x = –1 = 3,
a2
= P
(–1) / 2!
,
a3
=
P
(–1) / 3!
a4
= P
(4)(–1) / 4!
a5
=
P
(5)(–1) / 5!
Запишем искомое разложение:
x5 – 2x =
= 1+ 3 (x + 1) – 10 (x + 1)2 + 10 (x + 1)3 – 5 (x + 1)4 +
+(x + 1)5.
Первое приближение: x5 – 2x 1 + 3 (x + 1).
Это приближение с помощью дифференциала:
