
Variant15
.docВариант № 15
В задачах 1-9 найти общие решения уравнений и частные решения, если есть начальные условия.
1.
![]() .
Уравнение является однородным. Сделаем
замену
.
Уравнение является однородным. Сделаем
замену
![]() Тогда
Тогда
![]() .
Получим уравнение
.
Получим уравнение
![]() ,
или
,
или
![]() .
Разделяем переменные:
.
Разделяем переменные:
![]() .
Интегрируем уравнение:
.
Интегрируем уравнение:
![]() .
Получим:
.
Получим:
![]() или
или
![]() .
Вернёмся к переменной y,
делая обратную замену u=y/x:
.
Вернёмся к переменной y,
делая обратную замену u=y/x:
![]() .
Определим постоянную С из начальных
условий:
.
Определим постоянную С из начальных
условий:
![]() ,
отсюда C=π. Подставляя
это значение в общее решение, получим
частное решение:
,
отсюда C=π. Подставляя
это значение в общее решение, получим
частное решение:
![]() .
Ответ:
.
Ответ:
![]() .
.
2.
![]() .
Уравнение является линейным. Решим его
методом Бернулли. Будем искать решение
в виде произведения y=U∙V,
где U и V
неизвестные функции, определяемые в
данном случае уравнениями
.
Уравнение является линейным. Решим его
методом Бернулли. Будем искать решение
в виде произведения y=U∙V,
где U и V
неизвестные функции, определяемые в
данном случае уравнениями
![]() и
и
![]() .
Решим первое уравнение:
.
Решим первое уравнение:
![]() или
или
![]() .
Отсюда
.
Отсюда
![]() (произвольная постоянная добавляется
при решении второго уравнения). Потенцируя,
находим:
(произвольная постоянная добавляется
при решении второго уравнения). Потенцируя,
находим:
![]() .
Подставим найденную функцию U
во второе уравнение и решим его:
.
Подставим найденную функцию U
во второе уравнение и решим его:
![]() или
или
![]() .
Тогда
.
Тогда
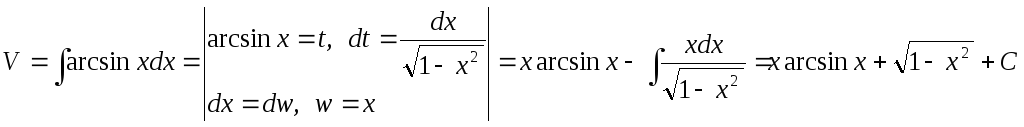 .
Таким образом, общее решение имеет вид:
.
Таким образом, общее решение имеет вид:
![]() .
Найдём C, исходя из
начальных условий:
.
Найдём C, исходя из
начальных условий:
![]() .
Тогда
.
Тогда
![]() .
Таким образом, частное решение есть
.
Таким образом, частное решение есть
![]() .
Ответ:
.
Ответ:
![]() .
.
3.
![]() .
Это уравнение Бернулли. Его можно решать
непосредственно как линейное уравнение,
применяя метод вариации произвольной
постоянной. Решим однородное уравнение:
.
Это уравнение Бернулли. Его можно решать
непосредственно как линейное уравнение,
применяя метод вариации произвольной
постоянной. Решим однородное уравнение:
![]() или
или
![]() .
Отсюда находим
.
Отсюда находим
![]() .
Будем предполагать, что решение исходного
уравнения имеет
.
Будем предполагать, что решение исходного
уравнения имеет
такую же структуру, но C=C(x),
т.е.
![]() ,
где C(x)
– некоторая неизвестная функция.
Определим эту функцию, подставляя данное
(предполагаемое) решение в исходное
уравнение. Найдём
,
где C(x)
– некоторая неизвестная функция.
Определим эту функцию, подставляя данное
(предполагаемое) решение в исходное
уравнение. Найдём
![]() .
.
Тогда
![]() .
Или
.
Или
![]() .
Разделяем переменные:
.
Разделяем переменные:
![]() .
Интегрируем уравнение:
.
Интегрируем уравнение:![]() .
Следовательно,
.
Следовательно,
![]() .
Общие решение уравнения
.
Общие решение уравнения
![]() .
Воспользуемся начальными условиями:
.
Воспользуемся начальными условиями:
![]() , т.е. C1=−1/2. Тогда
частным решением будет
, т.е. C1=−1/2. Тогда
частным решением будет
![]() .
Ответ:
.
Ответ:
![]() .
.
4.
![]() .
.
Найдём частные производные:
![]() ,
,
![]() .
Следовательно, уравнение является
уравнением в полных дифференциалах.
Левая часть этого уравнения представляет
полный дифференциал некоторой функции
U(x,y),
так что
.
Следовательно, уравнение является
уравнением в полных дифференциалах.
Левая часть этого уравнения представляет
полный дифференциал некоторой функции
U(x,y),
так что
![]() и
и
![]() .
Проинтегрируем второе уравнение по y:
.
Проинтегрируем второе уравнение по y:
![]() .
Таким образом,
.
Таким образом,
![]() ,
где φ(x) –
произвольная функция. Найдём эту функцию,
пользуясь первым уравнением. С одной
стороны
,
где φ(x) –
произвольная функция. Найдём эту функцию,
пользуясь первым уравнением. С одной
стороны
![]() .
С другой стороны,
.
С другой стороны,
![]() .
Приравнивая эти выражения, получим:
.
Приравнивая эти выражения, получим:
![]() .
Отсюда,
.
Отсюда,
![]() .
Согласно уравнению, dU=0.
Решением уравнения будет U(x,y)=C.
В данном случае
.
Согласно уравнению, dU=0.
Решением уравнения будет U(x,y)=C.
В данном случае
![]() .
Ответ:
.
Ответ:
![]() .
.
5.
 Уравнение второго порядка, допускающее
понижение порядка. В уравнении отсутствует
искомая функция y.
Сделаем замену
Уравнение второго порядка, допускающее
понижение порядка. В уравнении отсутствует
искомая функция y.
Сделаем замену
![]() .
Тогда
.
Тогда
![]() .
Получим уравнение Бернулли:
.
Получим уравнение Бернулли:
![]() .
Решим его методом Бернулли:
.
Решим его методом Бернулли:
![]() .
Функцию U найдём из
уравнения
.
Функцию U найдём из
уравнения
![]() .
Или
.
Или
![]() .
Функцию V найдём из
уравнения
.
Функцию V найдём из
уравнения
![]() .
Подставляя сюда функцию U,
получим:
.
Подставляя сюда функцию U,
получим:
![]()
![]() .
Или
.
Или
![]() Таким
образом,
Таким
образом,
![]() .
Определим постоянную C1,
пользуясь начальным условием
.
Определим постоянную C1,
пользуясь начальным условием
![]() :
:
![]() .
Следовательно,
.
Следовательно,
![]() .
Тогда
.
Тогда
![]() .
Или
.
Или
![]() .
Определим C2,
пользуясь вторым начальным условием
.
Определим C2,
пользуясь вторым начальным условием
![]() :
:
![]() .
Окончательно,
.
Окончательно,
![]() .
Ответ:
.
Ответ:
![]() .
.
6.
![]() Линейное неоднородное уравнение второго
порядка. Решим уравнение методом вариации
произвольных постоянных. Найдём сначала
решение однородного уравнения
Линейное неоднородное уравнение второго
порядка. Решим уравнение методом вариации
произвольных постоянных. Найдём сначала
решение однородного уравнения
![]() Характеристическое уравнение
Характеристическое уравнение
![]() имеет два равных корня:
имеет два равных корня:
![]() .
Получаем два частных решений:
.
Получаем два частных решений:
![]() .
Общее решение однородного уравнения
имеет вид:
.
Общее решение однородного уравнения
имеет вид:
![]() .
Будем считать, что решение неоднородного
уравнения имеет такую же структуру, но
С1 и С2 являются
функциями переменной х:
.
Будем считать, что решение неоднородного
уравнения имеет такую же структуру, но
С1 и С2 являются
функциями переменной х:
![]() .
Тогда, в соответствии с методом вариации
произвольных постоянных, неизвестные
функции С1(х) и С2(х)
определяются системой уравнений:
.
Тогда, в соответствии с методом вариации
произвольных постоянных, неизвестные
функции С1(х) и С2(х)
определяются системой уравнений:
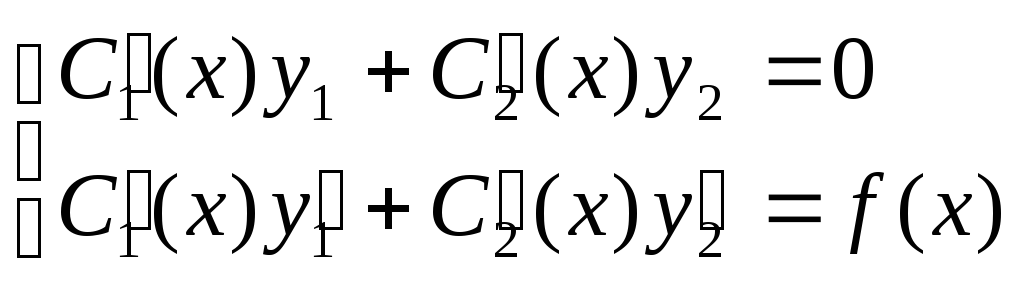 ,
где f(x)
– правая часть неоднородного уравнения.
В данном случае имеем систему:
,
где f(x)
– правая часть неоднородного уравнения.
В данном случае имеем систему:
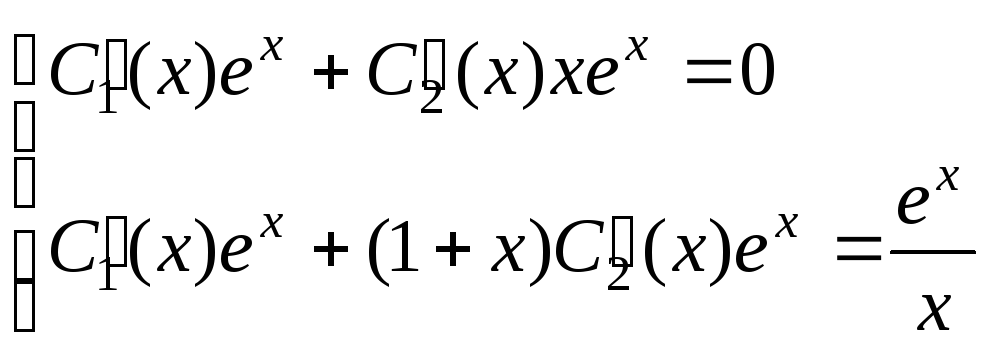 .
Поделим все уравнения на
.
Поделим все уравнения на
![]() :
:
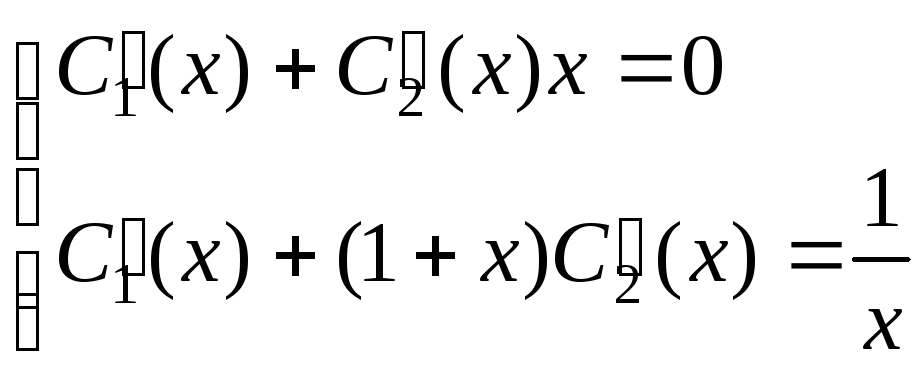 .
Решим систему методом Крамера:
.
Решим систему методом Крамера:
![]()
![]() .
Интегрируя, получаем:
.
Интегрируя, получаем:
![]() .
Следовательно, решением неоднородного
уравнения будет
.
Следовательно, решением неоднородного
уравнения будет
![]() .
Теперь можно вернуться к прежним
обозначениям произвольных постоянных.
Положим С3=С1 и
С4-1=С2. Окончательно,
.
Теперь можно вернуться к прежним
обозначениям произвольных постоянных.
Положим С3=С1 и
С4-1=С2. Окончательно,
![]() .
Ответ:
.
Ответ:
![]() .
.
7.
![]() .
Линейное неоднородное уравнение пятого
порядка. Найдём сначала решение
однородного уравнения
.
Линейное неоднородное уравнение пятого
порядка. Найдём сначала решение
однородного уравнения
![]() Характеристическое уравнение
Характеристическое уравнение
![]() ,
или
,
или
![]() ,
имеет пять корней:
,
имеет пять корней:
![]() .
Получаем четыре частных решений:
.
Получаем четыре частных решений:
![]() .
Общее решение однородного уравнения
имеет вид:
.
Общее решение однородного уравнения
имеет вид:
![]() .
Найдём частное решение неоднородного
уравнения, исходя из структуры его
правой части:
.
Найдём частное решение неоднородного
уравнения, исходя из структуры его
правой части:
![]() .
Здесь множитель х4 обусловлен
тем, что корень характеристического
уравнения r=0 совпадает
с коэффициентом α в экспоненте eαx,
«стоящей» в правой части уравнения
(α=0). Найдём производные yчн::
.
Здесь множитель х4 обусловлен
тем, что корень характеристического
уравнения r=0 совпадает
с коэффициентом α в экспоненте eαx,
«стоящей» в правой части уравнения
(α=0). Найдём производные yчн::
![]()
![]()
![]() . Подставим это в исходное уравнение:
. Подставим это в исходное уравнение:
![]() .
Отсюда находим
.
Отсюда находим
![]() .
Или
.
Или
![]() .
Следовательно,
.
Следовательно,
![]() .
Общее решение неоднородного уравнения
равно сумме общего решения однородного
уравнения и частного решения неоднородного:
.
Общее решение неоднородного уравнения
равно сумме общего решения однородного
уравнения и частного решения неоднородного:
![]() .
.
Ответ:
![]() .
.
8.
![]() .
Линейное неоднородное уравнение второго
порядка. Найдём сначала решение
однородного уравнения
.
Линейное неоднородное уравнение второго
порядка. Найдём сначала решение
однородного уравнения
![]() Характеристическое уравнение
Характеристическое уравнение
![]() имеет два корня:
имеет два корня:
![]() .
Получаем два частных решения:
.
Получаем два частных решения:
![]() .
Общее решение однородного уравнения
имеет вид:
.
Общее решение однородного уравнения
имеет вид:
![]() .
Найдём частное решение неоднородного
уравнения, исходя из структуры его
правой части:
.
Найдём частное решение неоднородного
уравнения, исходя из структуры его
правой части:
![]() .
Найдём производные yчн::
.
Найдём производные yчн::
![]() ,
,
![]()
![]() .
Подставим это в исходное уравнение:
.
Подставим это в исходное уравнение:
![]() .
Отсюда находим
.
Отсюда находим
![]() или
или
![]() .
Следовательно,
.
Следовательно,
![]() .
Общее решение неоднородного уравнения
равно сумме общего решения однородного
уравнения и частного решения неоднородного:
.
Общее решение неоднородного уравнения
равно сумме общего решения однородного
уравнения и частного решения неоднородного:
![]() .
Воспользуемся начальными условиями:
.
Воспользуемся начальными условиями:
![]() .
По первому условию
.
По первому условию
![]() .
Найдём
.
Найдём
![]() .
Тогда, по второму условию,
.
Тогда, по второму условию,
![]() .
Решая систему уранений, получим:
.
Решая систему уранений, получим:
![]() .
Частное решение уравнения будет
.
Частное решение уравнения будет
![]() .
.
Ответ:
![]() .
.
9.
![]() .
Линейное неоднородное уравнение второго
порядка. Найдём сначала решение
однородного уравнения
.
Линейное неоднородное уравнение второго
порядка. Найдём сначала решение
однородного уравнения
![]() .
Характеристическое уравнение
.
Характеристическое уравнение
![]() имеет два корня:
имеет два корня:
![]() .
Получаем два частных решения:
.
Получаем два частных решения:
![]() .
Общее решение однородного уравнения
имеет вид:
.
Общее решение однородного уравнения
имеет вид:
![]() .
Найдём частное решение неоднородного
уравнения, исходя из структуры его
правой части:
.
Найдём частное решение неоднородного
уравнения, исходя из структуры его
правой части:
![]() .
Найдём производные yчн::
.
Найдём производные yчн::
![]() ,
,
![]() .
Подставим это в исходное уравнение:
.
Подставим это в исходное уравнение:
![]()
![]() .
Приравнивая коэффициенты при одинаковых
функциях в левой и правой частях
равенства, получим:
.
Приравнивая коэффициенты при одинаковых
функциях в левой и правой частях
равенства, получим:
![]() .
Или:
.
Или:
![]() .
Следовательно,
.
Следовательно,
![]() .
Общее решение неоднородного уравнения
равно сумме общего решения однородного
уравнения и частного решения неоднородного:
.
Общее решение неоднородного уравнения
равно сумме общего решения однородного
уравнения и частного решения неоднородного:
![]() .
.
Ответ:
![]() .
.
10. Решить систему линейных однородных
дифференциальных уравнений первого
порядка с постоянными коэффициентами
![]() ,
где
,
где
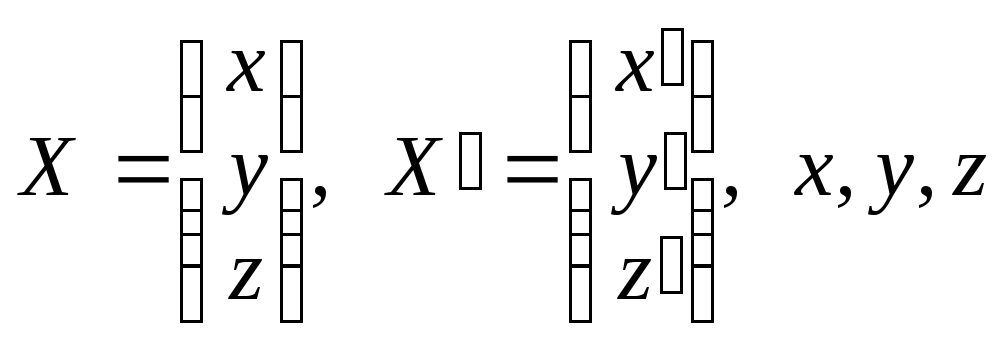 -
функции от t, M
– матрица коэффициентов, при начальных
условиях
-
функции от t, M
– матрица коэффициентов, при начальных
условиях
![]() :
:
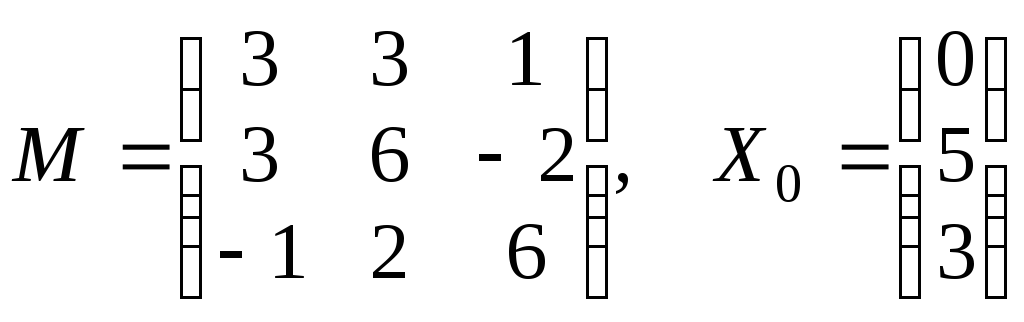 .
.
Запишем систему по исходным данным:
 .
Ищем решение в виде
.
Ищем решение в виде
 .
Тогда
.
Тогда
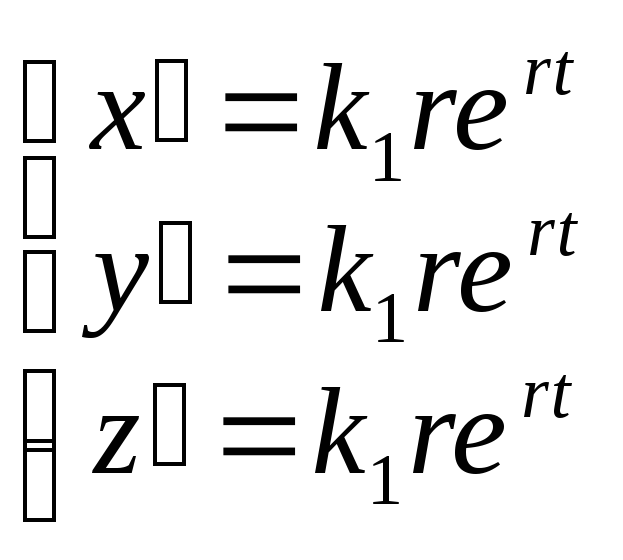 .
Подставляя это в систему, получим систему
алгебраических уравнений, которая
определяет неизвестные коэффициенты
.
Подставляя это в систему, получим систему
алгебраических уравнений, которая
определяет неизвестные коэффициенты
![]() :
:
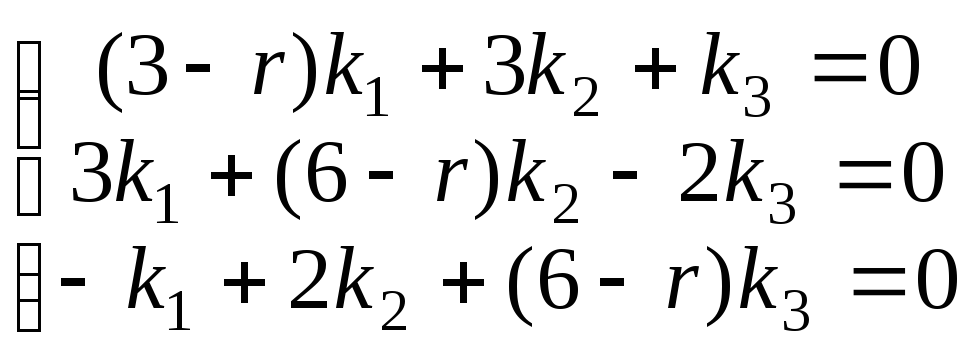 .
Приравнивая определитель системы к
нулю, получим характеристическое
уравнение исходной системы:
.
Приравнивая определитель системы к
нулю, получим характеристическое
уравнение исходной системы:
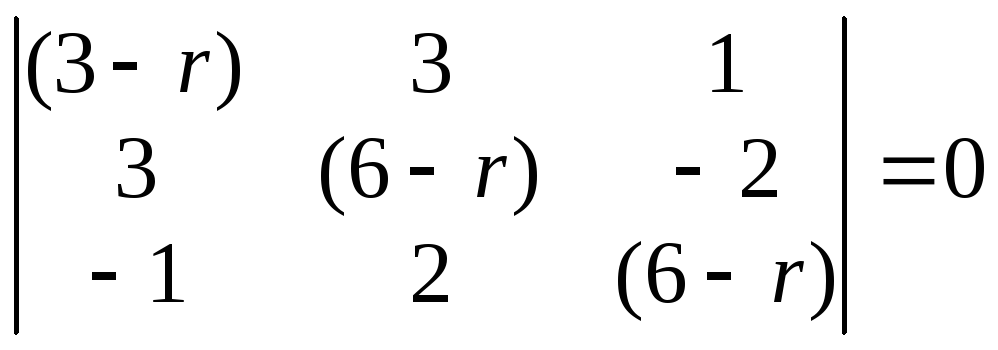 .
Раскроем определитель:
.
Раскроем определитель:
![]() .
Или
.
Или
![]() .
Следовательно,
.
Следовательно,
![]() .
При
.
При
![]() получим систему:
получим систему:
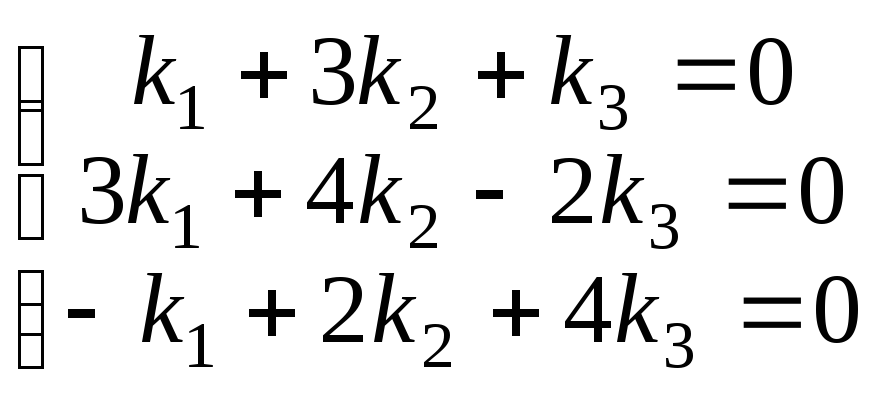 .
Отбросим второе уравнение, как линейно
зависимое. Получим
.
Отбросим второе уравнение, как линейно
зависимое. Получим
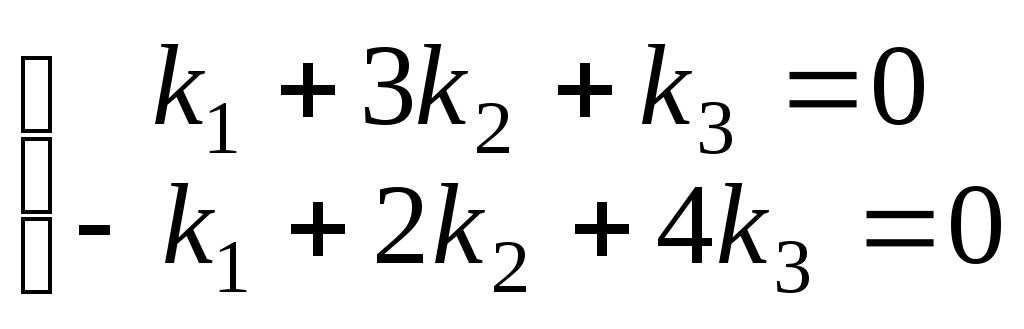 .
Положим
.
Положим
![]() .
Тогда
.
Тогда
![]() .
Получили первое частное решение:
.
Получили первое частное решение:
![]() .
При
.
При
![]() получим систему:
получим систему:
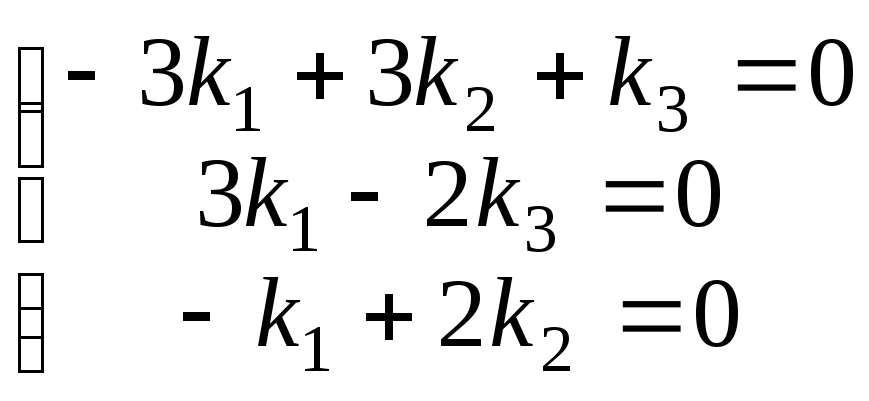 .
Отбросим первое уравнение, как линейно
зависимое. Получим
.
Отбросим первое уравнение, как линейно
зависимое. Получим
 .
Положим
.
Положим
![]() .
Тогда
.
Тогда
![]() .
Получили второе частное решение:
.
Получили второе частное решение:
![]() .
.
При
![]() получим систему:
получим систему:
 .
Отбросим второе уравнение, как линейно
зависимое. Получим
.
Отбросим второе уравнение, как линейно
зависимое. Получим
 .
Положим
.
Положим
![]() .
Тогда
.
Тогда
![]() .
Получили третье частное решение:
.
Получили третье частное решение:
![]() .
Общее решение записывается как линейная
комбинация частных решений:
.
Общее решение записывается как линейная
комбинация частных решений:
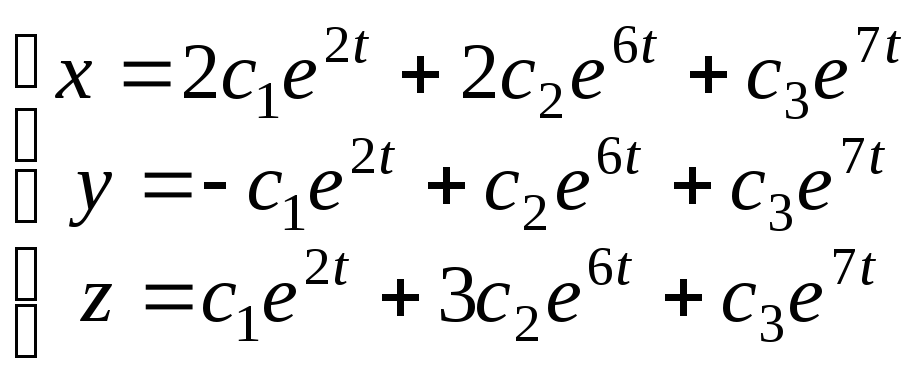 .
.
Найдём произвольные постоянные, пользуясь
начальными условиями. При t=0
получим систему:
 .
Вычитая из первого уравнения второе,
затем из первого уравнения третье,
получим:
.
Вычитая из первого уравнения второе,
затем из первого уравнения третье,
получим:
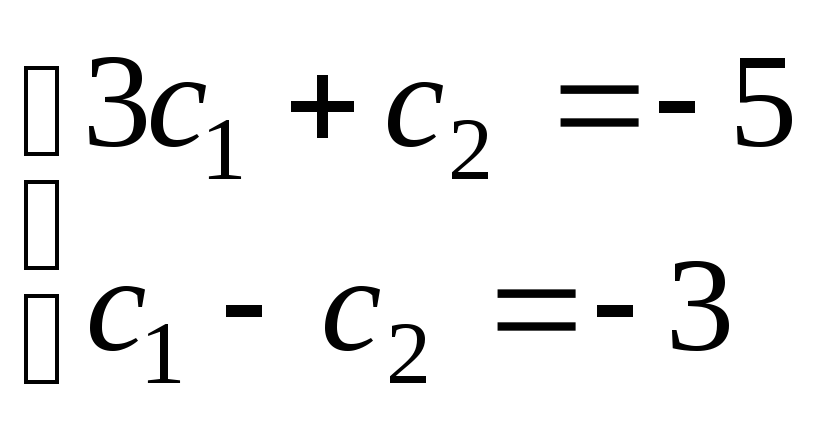 .
Следовательно,
.
Следовательно,
![]() .
Таким образом, частное решение системы
следующее:
.
Таким образом, частное решение системы
следующее:
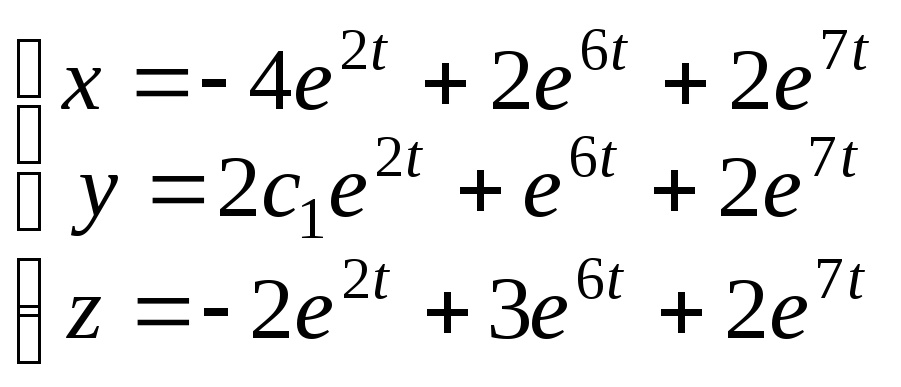 .
Ответ:
.
Ответ:
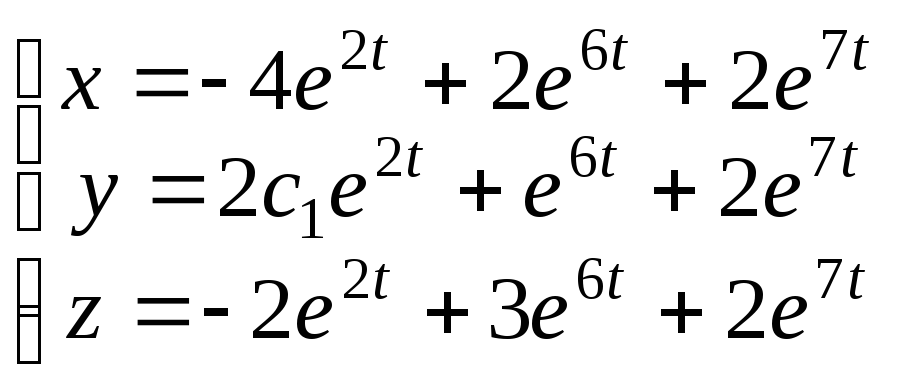 .
.
11. Найдите уравнение кривой, проходящей через точку M(3; 4) и обладающей свойством, что отрезок, отсекаемый любой касательной на оси ординат, равен удвоенному модулю радиус-ыектора точки касания.
Уравнение касательной к кривой
![]() в точке
в точке
![]() имеет вид
имеет вид
![]() .
Найдём точки пересечения касательной
с осью ОУ. Положим x=0.
Тогда
.
Найдём точки пересечения касательной
с осью ОУ. Положим x=0.
Тогда
![]() или
или
![]() .
Точка М1
.
Точка М1
![]() является точкой пересечения оси ОУ. По
условию задачи
является точкой пересечения оси ОУ. По
условию задачи
![]() .
Это равенство справедливо для любой
точки
.
Это равенство справедливо для любой
точки
![]() .
Заменим эту точку произвольной точкой
.
Заменим эту точку произвольной точкой
![]() ,
лежащей на кривой
,
лежащей на кривой
![]() .
Получим:
.
Получим:
![]() ,
или
,
или
![]() ,
или
,
или
![]() .
Это однородное уравнение. Положим
.
Это однородное уравнение. Положим
![]() .
Тогда
.
Тогда
![]() .
Или
.
Или
![]() .
При знаке «+» получим:
.
При знаке «+» получим:
![]() .
Найдём C, учитывая,
что кривая проходит через точку М(3, 4):
.
Найдём C, учитывая,
что кривая проходит через точку М(3, 4):
![]() .
Таким образом,
.
Таким образом,
![]() .
При знаке «-» получим:
.
При знаке «-» получим:
![]() .
Найдём C, учитывая,
что кривая проходит через точку М(3, 4):
.
Найдём C, учитывая,
что кривая проходит через точку М(3, 4):
![]() .
Таким образом,
.
Таким образом,
![]() .
.
Ответ:
![]() .
.
-
Во фляжку ёмкостью 1 л по трубке втекает кислород, и смесь с находившимся там воздухом, равномерно перемешиваясь, вытекает через другую трубку. Считая, что в нормальном состоянии воздух содержит 21% кислорода, найдите процент кислорода во фляжке после того, как сквозь неё протечёт 5 л газа.
Пусть
![]() доля кислорода в смеси, если во фляжку
втекло
доля кислорода в смеси, если во фляжку
втекло
![]() л кислорода. Тогда
л кислорода. Тогда
![]() ,
где V – объём фляжки.
Пусть во фляжку поступило дополнительно
,
где V – объём фляжки.
Пусть во фляжку поступило дополнительно
![]() л кислорода, при этом вытекло
л кислорода, при этом вытекло
![]() л смеси. Вместе со смесью вытекло
л смеси. Вместе со смесью вытекло
![]() л кислорода. Следовательно, доля кислорода
станет равной
л кислорода. Следовательно, доля кислорода
станет равной
![]() .
Приращение доли кислорода составит
величину
.
Приращение доли кислорода составит
величину
![]() .
Поделив на
.
Поделив на
![]() и перейдя к пределу при
и перейдя к пределу при
![]() ,
получим:
,
получим:
![]() .
Так как V =1, то
.
Так как V =1, то
![]() .
Решим уравнение:
.
Решим уравнение:
![]()
![]() При
При
![]() доля кислорода была равной 0,21. Тогда
доля кислорода была равной 0,21. Тогда
![]() .
После протекания 5 л газа, получим:
.
После протекания 5 л газа, получим:
![]() ,
что составляет 99,5%. Ответ: 99,5%.
,
что составляет 99,5%. Ответ: 99,5%.
