TR_4_задачи_5-10.doc / TR_4_задачи_5-10

ЗАМЕЧАНИЕ. При решении следующих задач будут использованы термины, которые мы сейчас введем.

Область (D) плоскости будем называть y-трапецией, если она может быть задана системой неравенств вида a x b, y₁(x)  y y₂(x). Такая область допускает удобную штриховку вертикальными отрезками: все их нижние концы лежат на кривой y = y₁(x), все верхние на кривой y y₂(x) (рис.71).

Аналогично введем понятие x-трапеции: c y d, x₁(y)  x x₂(y). (рис.71). Для x-трапеции удобна горизонтальная штриховка.

Рис.71

В случае y-трапеции =;

в случае x-трапеции =.

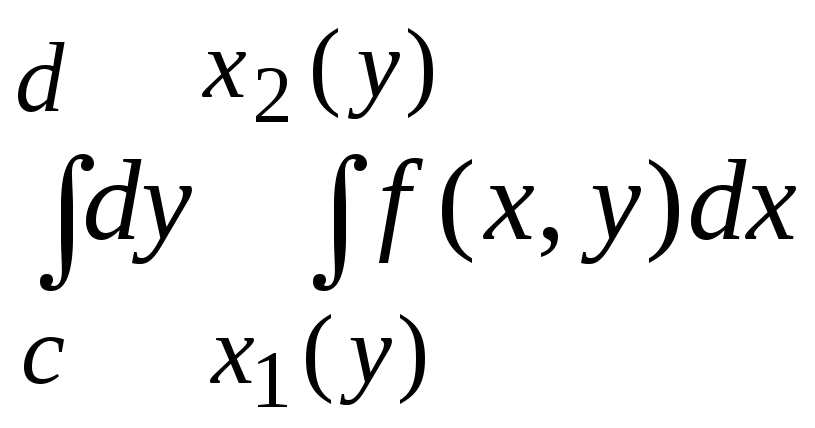Тело (T) в пространстве назовем z-брусом, если оно может быть задано следующим образом: (x, y)D длянекоторой области D в плоскости , ограниченной замкнутой кусочно-гладкой кривой, z₁(x,y)  z z₂(x,y). Каждый z-брус может быть “заполнен” отрезками ,параллельными оси , нижние концы которых лежат на поверхности z z₁(x,y) ”дне”, а верхние  на поверхности z z₂(x,y) ”крышке”. Аналогично введем понятия y-бруса и x-бруса (рис.72).

В случае z-бруса .

Рис.72

ЗАДАНИЕ 5. Изменить порядок интегрирования в интеграле

.

РЕШЕНИЕ.

Восстановим область интегрирования () по пределам повторных интегралов: =₁₂,

(₁): ;

(₂):

Изобразим область интегрирования на чертеже. Найдем точки пересечения параболы и прямой : т.е. точкам пересечения кривых соответствуют точки, для которых и . Вертикальной штриховкой покажем порядок интегрирования: сначала по y при фиксированном x. Сменим штриховку на горизонтальную. Из рисунка видно, что данная область является -трапецией.

Рис.73

Уравнение “нижней” кривой есть , “верхней” - прямая . Поэтому (): и в результате подстановки пределов получим следующий повторный интеграл:

Ответ.

ЗАДАНИЕ 6. Найти объем тела, ограниченного поверхностями

; .

РЕШЕНИЕ.

Тело ограничено с “боков” плоскостью и цилиндром (цилиндрической поверхностью) . “Снизу” тело “накрыто” плоскостью , сверху – плоскостью . Изобразим на чертеже заданное тело (рис.74).

Рис.74

Очевидно, тело есть - цилиндрический брус. Область (), являющуюся ортогональной проекцией тела на плоскость , изобразим на отдельном рисунке. Для этого найдем точки пересечения параболы с прямой . Опуская подробности вычислений, получим, что прямая и “положительная” ветвь параболы пересекаются в точке, в которой . Объем цилиндрического бруса может быть найден с помощью двойного интеграла. Учитывая, что тело “стоит” на плоскости , для объема запишем формулу и перейдем к повторному интегралу. Область (), изображенная на рисунке, очевидно не является - трапецией, но является - трапецией:

(): .

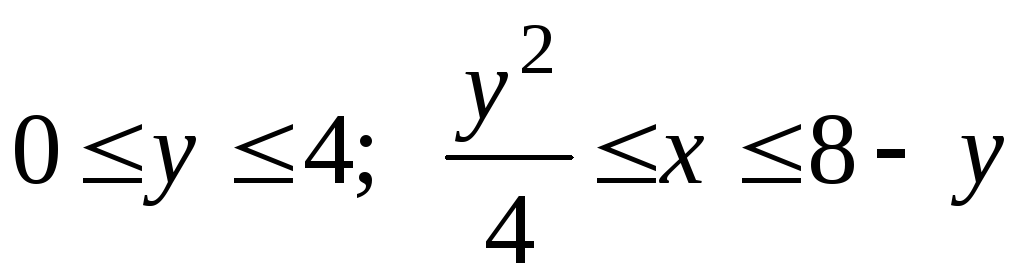Записав объем через повторный интеграл и производя вычисления, последовательно получим

V=.

Ответ. Объем тела равен 80.

ЗАДАНИЕ 7. Найти объем тела, ограниченного указанными поверхностями.

Приведем решение двух задач на вычисление объемов тел, рассматривая тела с различной геометрией поверхности.

1) ,

2) .

РЕШЕНИЕ.

1). Тело ограничено двумя поверхностями: параболоидом и плоскостью . Изобразим это тело на чертеже (рис.75).

Рис.75

Данное тело является -цилиндрическим брусом (рис.72); боковая поверхность выродилась в линию пересечения заданных поверхностей. Найдем область, в которую тело проектируется на плоскость , для чего из уравнений поверхностей, ограничивающих тело, следует исключить переменную (т.е. совершить ортогональное проектирование):

и .

Таким образом, областью () является круг с центром в точке (0; 1) радиуса =1 (см. рис.75).

Объем тела может быть вычислен с помощью тройного интеграла по формуле . В декартовой системе координат тройной интеграл записывается через повторный следующим образом:

,

откуда видно, что его вычисление сопряжено со значительными трудностями (на завершающей стадии вычисления повторного интеграла).

Запишем интеграл в цилиндрической системе координат , с которой декартова система связана формулами

.

Якобиан преобразования . Формула перехода (в интеграле) имеет вид

.

В нашем случае

.

Запишем уравнения параболоида и плоскости в цилиндрической системе координат:

; .

Для окружности имеем ; угол , очевидно, необходимо менять в пределах от 0 до . Таким образом ,

===.

Ответ. =.

2) Изобразим тело , ограниченное поверхностями цилиндра , параболоида и плоскостью (рис.76).

Рис.76

Замечание. При построении следует преобразовать уравнение направляющей цилиндра , лежащей в плоскости к каноническому виду (прибавляя и вычитая 2): , откуда получим , то есть направляющей цилиндра в плоскости служит окружность с центром в точке радиуса . Кроме того, при построении следует учесть, что поверхность параболоида пересекается с плоскостью по окружности . Тело является z-цилиндрическим брусом, проектирующимся на плоскость в область (), являющуюся -трапецией.

Нетрудно убедиться, что и здесь, как и в предыдущем случае, повторный интеграл, записанный в декартовой системе координат, при вычислении требует значительных усилий; поэтому и в этом случае перейдем к цилиндрической системе координат (см. предыдущую задачу):

.

Найдем уравнения поверхностей, ограничивающих тело, в цилиндрической системе координат: уравнение цилиндра перейдет в , уравнение параболоида – в , плоскости – в . Область (), являющаяся проекцией тела на плоскость , ограничена окружностью и окружностью (так как ). Найдем значения параметра , соответствующие точкам пересечения этих окружностей: , откуда и для получим два значения: . Учитывая симметрию тела относительно плоскости , объем запишем в виде следующего повторного интеграла:

.

Приведем вычисление объема:

=

=

=.

Ответ. .

ЗАДАНИЕ 8. Найти объем тела , ограниченного поверхностями

а) ; б) ; в) .

РЕШЕНИЕ.

Изобразим тело, ограниченное двумя концентрическими сферами с центрами в начале координат и радиусами 8 и 12 и (“снизу”)  конусом ; от полученного таким образом тела плоскостями и “отрезается” заданное условием задачи тело (V) (рис.77) .

Рис.77

Объем тела может быть вычислен по формуле . Рассматривая тело в декартовой системе координат, видим, что оно не является ни -, ни -, ни -цилиндрическими брусами (см. рис.72); разбиение тела на z- цилиндрические бруски является само по себе не простой задачей, не говоря уже о вычислении повторных интегралов. “Конструкция” тела такова, что вычисление тройного интеграла удобнее провести в сферической системе координат r,, связанной с декартовой системой координат формулами:

; ; .

Якобиан такого преобразования . Для объема получим:

.

Чтобы тройной интеграл записать в виде повторного, перейдем в уравнениях ограничивающих тело поверхностей к сферическим координатам. Следует использовать соотношения

.

Уравнение переходит в , уравнение  в ; для уравнения конуса получим последовательно: , и , откуда и ; уравнение плоскости переходит в уравнение , уравнение плоскости в , т.е. в . Таким образом,

.

Так как подынтегральная функция представляет собой произведение функций, каждая из которых зависит только от одной переменной, а пределы интегрирования постоянны, то повторный интеграл представляет собой просто произведение трех интегралов

;

==;

.

Для объема тела получим

.

Ответ. .

ЗАДАНИЕ 9. Найти массу пластинки

(): ,

Плотность массы пластинки

РЕШЕНИЕ. Область () – это часть эллиптического кольца (на рис.78 область () заштрихована). Массу плоской области можно вычислить по формуле . Подставляя заданную плотность в двойной интеграл, для массы получим .

Рис.78

Очевидно, что область () не является ни -, ни - трапецией; при вычислении двойного интеграла в декартовой системе координат область () пришлось бы разбить на три области. Как для областей, заключенных между концентрическими окружностями с центром в начале координат “родной” является полярная система координат, так и для эллиптических колец “своей “ является эллиптическая система координат (обобщенная полярная система координат)

; .

Выбор обусловлен соображениями удобства при вычислении интегралов. Положим для заданной области :

; .

Якобиан преобразования вычисляется по формуле .

Совершим преобразование области (): уравнение эллипса перейдет в , т.е.  эллипс преобразуется в

окружность радиуса 1; эллипс переходит в окружность ; прямая  в луч , прямая  в луч (действительно, и ). Запишем двойной интеграл в обобщенной полярной системе координат:

.

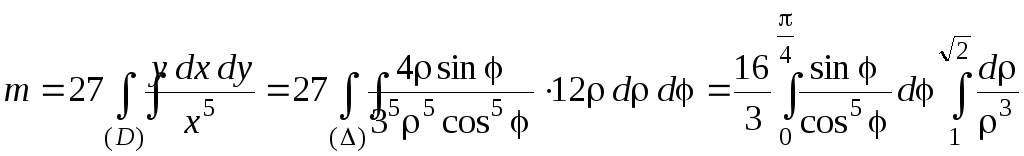В данном случае повторный интеграл есть произведение двух определенных интегралов, так как внутренний интеграл по есть скаляр. Вычислим их:

;

.

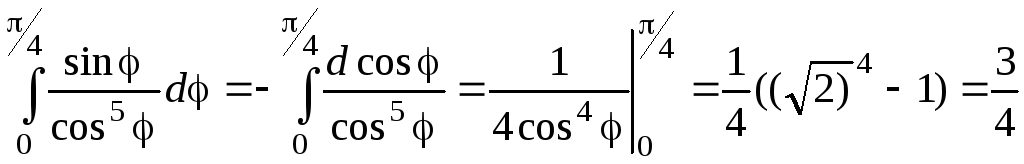Таким образом, .

Ответ. Масса пластинки равна 1.

ЗАДАНИЕ 10. Найти массу тела , ограниченного поверхностями: ; ; ; ; плотность массы тела .

РЕШЕНИЕ.

Область ограничена с боков координатными плоскостями и цилиндрической поверхностью . Снизу она “накрыта” плоскостью , сверху  поверхностью параболоида (рис.79).

Рис.79

Область является -цилиндрическим брусом. Масса тела может быть вычислена по формуле:

.

Цилиндрический брус проектируется на плоскость в криволинейную трапецию (D): 0 x 1, 0 y . Преобразуем тройной интеграл в повторный и вычислим его:

=

=[ замена переменных ; ; ; ]=