2631761_42.1412840525.10196

Это заблуждение, в чем позволяет убедиться следующий пример. ПРИМЕР 1.3.1. На рынке некоторого товара функция предложения

S(p) = 2p – 2, а функция спроса D(p) = 10 – p. Требуется определить, во сколько раз изменится равновесная цена товара, реализованный спрос и выручка производителя при введении акциза по ставке t (0; 1) . Получен-

ные формулы нужно интерпретировать при установлении ставки акциза на уровне 1, 5, 20, 50 и 90%.

Решение. Вначале из условия (1.3.1) найдем равновесную цену до введения акциза:

Таким образом, в условиях рассматриваемого примера на потребителя ложится бремя оплаты двух третей введенного налога, а оставшуюся треть платит производитель.

Чтобы выяснить, на сколько процентов вырастает цена при введении акциза, преобразуем последнее выражение:

Отсюда следует, что введение акциза при ставке t = 1% = 0,01 приводит к незначительному увеличению цены — на

введение 5%-ного акциза приводит к увеличению цены на

21

для ставок, равных 20, 50 и 90%, получаем соответственно увеличение це-

ны на 15,4, 50 и 150%.

Естественно, увеличение цены приводит к уменьшению объема реализованного спроса и предложения, и как следствие, к уменьшению выручки производителя. До введения налога в точке равновесия реализовывался спрос

D ( p0 ) = 10 - p0 = 6 ед.,

с введением акциза спрос стал равен

Найдем отношение нового и старого значений спроса:

При ставке акциза t = 1% из последнего выражения следует, что спрос снижается на

при 5%-ной ставке аналогичный расчет показывает уменьшение спроса после введения налога на

для ставок, равных 20 и 50%, получаем соответственно снижение спроса на 10,3 и 33,3%, а при 90%-ном акцизе в данном примере спрос полностью исчезает:

4 × 0,9 = =

1 100%.

9 - 6 ×0,9

Теперь посмотрим, как изменится выручка производителя при введении акциза.

До введения акциза выручка равна

p0 D ( p0 ) = 4 × 6 = 24 ден. ед.,

после введения акциза выручка (с учетом уплаты налога) изменяется до

22

Таким образом, при ставке акциза t = 1% выручка уменьшается на

0,01(7 - 6 × 0,01) » 0,8%, (3 - 2 × 0,01)2

при 5%-ной ставке аналогичный расчет показывает уменьшение спроса после введения налога на

для ставок, равных 5, 20 и 50%, получаем соответственно снижение выручки на 4,0, 17,2 и 50,0%. При 90%-ном акцизе в данном примере выручка будет равна нулю.

Теперь посмотрим на ту же ситуацию с точки зрения государства. ПРИМЕР 1.3.2. В условиях примера 1.3.1 требуется найти такую став-

ку акциза, которая обеспечит максимум налоговых поступлений. Решение. Чтобы определить ставку акциза, максимизирующую

налоговые поступления, поставим такую задачу:

pt > 0, 0 < t <1,

которую, учитывая конкретный вид функции спроса из условия примера (D(p) = 10 – p), а также выражение для равновесной цены после введения акциза (1.3.3), преобразуем к виду

0 < t <1.

23

Вычисляем производную:

определяем критические точки: 9/14 и 3/2, находим промежутки возрастания: (−∞; 9 / 14] и (3 / 2; + −∞) и промежуток убывания [9 / 14; 3 / 2) . Это

дает возможность определить точку максимума функции T (t ) : t = 9 / 14 .

Поскольку данная точка глобального максимума принадлежит интервалу (0; 1), значение t = 9 / 14 ≈ 64% и является решением задачи (1.3.4).

При такой ставке акциза равновесная цена равна

это на 75% выше, чем на рынке без акциза; равновесный спрос составляет

D(p )=10 −7 = 3 ед. —

это в два раза меньше, чем на рынке без акциза. При этом налоговые поступления составляют

что на 69% меньше, чем до введения акциза. Посмотрим теперь, как введение акциза повлияет на оптимальное

решение задачи производителя (1.2.3). После введения акциза (по ставке t) выражение для прибыли производителя изменится по сравнению с (1.2.3):

Π( K , L) = (1 − t ) F ( K , L) − pK K − pL L .

Запишем необходимые условия максимума прибыли:

24

У неоклассических производственных функций первые производные положительны, а вторые — отрицательны (см. параграф 1.1), поэтому ∂F ( K , L ) / ∂K и ∂F ( K , L ) / ∂K — положительные убывающие функции.

Отсюда следует, что максимум прибыли при наличии акциза достигается при меньших затратах и труда, и капитала, и как следствие, при меньших объемах производства.

Перейдем теперь к рассмотрению налога на прибыль. Поскольку налог на прибыль не изменяет условие рыночного равновесия (1.3.1), он не изменяет равновесных рыночных цен, значений спроса и предложения.

Точно такой же вывод можно получить из сравнения задачи

Π(K , L) = (1 − t) ( F (K , L) − pK K − pL L )

сзадачей (1.2.3): условия максимума прибыли в этих задачах совпадают. Таким образом, между акцизом и налогом на прибыль есть суще-

ственные различия. В отличие от налога на прибыль, который является только инструментом перераспределения части доходов от успешных производителей в пользу государства, акциз является также инструментом рыночного регулирования, позволяя не только перераспределять доходы, но и регулировать объемы производства товаров.

§1.4. МОДЕЛЬ УПРАВЛЕНИЯ ЗАПАСАМИ

Втрадиционной экономике материальных товаров предприятия тратят значительные ресурсы на содержание складских запасов, и перед такими предприятиями стоит важная задача управления запасами с целью предотвращения как дефицита, так и избытков.

Обсудим модель управления запасами, основная цель которой — определение оптимального размера заказываемой партии и оптимальной частоты заказов.

Будем считать, что производственные потребности v в единицу времени являются постоянным, заказанная партия доставляется одновременно, затраты K на организацию поставки постоянны и не зависят от размера q заказываемой партии, а издержки содержания единицы сырья составляют s за единицу времени.

Уровень запаса снижается равномерно от q до нуля, после чего подается заказ на доставку новой партии сырья величиной q. Заказ выполняется мгновенно, и уровень запаса восстанавливается до величины q. Зависимость уровня запаса I от времени t иллюстрируется рис. 1.4.1.

25

I

q

Рис. 1.4.1. Динамика уровня запасов

Интервал времени длиной τ называется циклом запаса. Длина цикла равна, очевидно, τ = q/v, средняя величина запаса равна q/2. Поэтому издержки в течение цикла L состоят из стоимости заказа K и затрат по содержанию запаса:

L = K + s q τ .

2

Издержки в единицу времени l получим, разделив издержки в течение цикла L на длину цикла τ :

Оптимальный размер заказываемой партии определим из необходимого условия максимума функции l(q) — равенства нулю первой производной:

l′(q) = s − Kv = 0 ,

2 q2

откуда

Учитывая неотрицательность размера заказа, окончательно получаем, что оптимальный размер заказываемой партии должен составлять

26

затраты в единицу времени при такой стратегии будут равны

ПРИМЕР 1.4.2. Мебельная фабрика использует в своем производстве фанеру. Еженедельно требуется 200 листов фанеры, затраты на организацию каждой поставки равны 8000 руб., издержки содержания одного листа фанеры на складе равны 20 руб. в неделю. Требуется определить оптимальный размер заказываемой партии фанеры и цикл заказа.

Решение. По условию v = 200, K = 8000, s = 20. Используя формулы

(1.4.1)—(1.4.2), получаем:

Таким образом, каждые две недели следует заказывать по 400 листов фанеры.

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ

1.Каково соотношение между предельными и средними эффективностями использования ресурсов в случае, если экономическая система описывается: а) линейной производственной функцией; б) производственной функцией Леонтьева?

2.Какова предельная норма замены труда капиталом в экономической системе, которая описывается: а) мультипликативной производ-

ственной функцией; б) линейной производственной функцией; в) производственной функцией Леонтьева.

3.Постройте на одном рисунке графики нескольких изоквант (т. е. линий, на которых выпуск не изменяется) для следующих производственных функций: а) мультипликативной; б) линейной; в) Леонтьева.

4.Постройте на одном рисунке графики нескольких изоклиналей (т. е. линий наибольшего роста выпуска) для следующих производственных функций: а) мультипликативной; б) линейной; в) Леонтьева.

27

5.Какой экономический смысл имеют коэффициенты cK и cL линейной производственной функции?

6.Объем ежемесячного выпуска продукции завода в денежном выражении составляет 10 млн. руб., стоимость основных производственных фондов этого завода также равна 10 млн. руб., а численность занятых равна 1 тыс. человек Найдите производственную функцию Кобба — Дугласа данного завода.

7.Выпуск продукции X (т/ч) определяется только количеством занятых рабочих K (чел./ч): X = F ( K ) , при этом единственным видом из-

держек является заработная плата. Найдите функцию спроса на труд

— зависимость оптимальной численности занятых от цены продук-

ции p и заработной платы w в случае, когда F ( K ) = 6 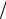K ;

б) F (K ) = ln(K + 2) .

8.Прибыль фирмы следующим образом зависит от затрат капитала K и затрат труда L: Π = −4 K 2 + 24 K + 2 KL − 6 L − L2 . Найдите такие размеры затрат капитала и труда, при которых прибыль будет максимальной.

9.Стоимость размещения рекламного баннера на популярном портале составляет 50 тыс. руб. в день, а стоимость показа минутного ре-

кламного ролика по телевидению равна 150 тыс. руб. Бюджет фирмы предусматривает еженедельные расходы на рекламу в размере 1,5 млн. руб. Прибыль фирмы зависит от количества дней размещения баннера на портале x1 и количества показов ролика по телевиде-

нию x21 следующим образом: X = 4 x1 x2 − 50 − x22 + 20 x1 + 1 000 000 . Как оптимально распорядиться рекламным бюджетом?

10.Издержки фирмы зависят от объема выпуска: C ( X ) = X 2 + 2 X + 3 .

Цена, по которой фирма реализует продукцию, также зависит от объема выпуска: P ( X ) = 200 − 2 X . Найдите оптимальный объем

выпуска в трех ситуациях: а) налоги не взимаются; б) взимается 20%-ный налог на прибыль; в) взимается 20%-ный акциз.

11.В среднем магазин продает 300 чайников данной модели. Наклад-

ные расходы по заказу доставки партии чайников составляют 10 000 руб., себестоимость хранения одного чайника на складе равна 300 руб./мес., дефицит чайников не допускается. Найдите оптимальный размер заказываемой партии чайников данной марки, интервал между заказами и месячные издержки магазина по доставке и хранению чайников данной модели.

28

ГЛАВА 2. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ И БАЛАНСОВЫЕ МОДЕЛИ ЭКОНОМИКИ

§ 2.1. ВЕКТОРЫ И МАТРИЦЫ

Совокупность n чисел a1, a2 , …, an , заданных в определенном порядке, называется n-мерным вектором. Числа ai называются компонента-

ми или координатами вектора, число n — его размерностью. Обозначают вектор одной жирной строчной латинской буквой:

a = (a1, a2 , …, an )

[на доске и в тетради, конечно, жирный шрифт не используется, но чтобы не возникало путаницы, можно над буквами, обозначающими векторы, ставить черточки или стрелочки: a = (a1 , a2 , …, an ) или a = (a1, a2 , …, an ) ].

Например, x = (9, − 2, 4, − 7, 0, 3) — это шестимерный вектор.

Допустим, что предприятие выпускает n видов продукции, притом предполагается изготовить продукцию первого вида в количестве X1 шт.,

второго вида в количестве x2 шт. и т. д. В этом случае п р о и з в о д - с т в е н н у ю п р о г р а м м у

( x1 , x2 , …, xn )

можно рассматривать как n-мерный вектор.

Два n-мерных вектора a и b называются равными, если все их соответствующие компоненты равны:

ai = bi , i =1, 2, …, m .

Суммой двух n-мерных векторов a = (a1, a2 , …, an ) и b = (b1 , b2 , …, bn ) называется n-мерный вектор

(a1 + b1, a2 + b2 , …, an + bn ) ,

компоненты которого получаются сложением соответствующих компонент данных векторов.

29

Предположим, например, что производственное объединение состоит из двух мебельных фабрик, которые выпускают столы, стулья, кресла и кровати. Пусть первая фабрика выпускает 1000 столов, 10 000 стульев, 2000 кресел и 500 кроватей в год, а вторая фабрика — 2500 столов, 12 000 стульев, 2000 кресел и 1000 кроватей в год. Тогда объем годового выпуска первой фабрики представляет собой вектор a = (1000, 10 000, 2000, 500) , объем годового вы-

пуска второй фабрики — это вектор b = (2500, 12 000, 2000, 1000) , при этом объем годового выпуска всего объединения равен сумме векторов a и b:

a + b = (3500, 22 000, 4000, 1500) .

Операция сложения векторов обладает свойствами коммутативно-

сти и ассоциативности:

Вектор

θ = (0, 0, …, 0) ,

все компоненты которого равны нулю, называется нуль-вектором. Каков бы ни был вектор a , справедливо равенство

т. е. нуль-вектор ведет себя при сложения векторов аналогично числу нуль в арифметике.

Операция вычитания векторов определяется как сложение с противоположным вектором

a − b = a + (−b) ,

Под произведением вектора a = (a1, a2 ,…, an ) на число λ понимают

вектор

(λa1 , λa2 , …, λan ) ,

компоненты которого получаются умножением всех компонент данного вектора на данное число, и обозначают λa или aλ. Например, если первая из рассмотренных мебельных фабрик пожелает увеличить свой выпуск в два раза, то это будет означать, что новый годовой план производства бу-

дет задаваться вектором 2a = (2000, 20 000, 4000, 1000) .

30