2631761_42.1412840525.10196

1.Пункты X0 и X8 связаны сетью дорог, проходящих через промежуточные пункты. Стоимость проезда из пункта Xi в пункт Xj указана на графе. Определите минимальную стоимость проезда из X0 и X8.

251

2.Основу строительства объекта составляют 12 операций, последовательность выполнения и продолжительность которых задана в таблице. Составьте сетевой график проекта и определите критический путь и скорейшее время завершения всего проекта.

3.Какой максимальный поток газа можно пропустить из пункта X1 в пункт X8 в единицу времени по сети газопровода, пропускные способности промежуточных дуг которого приведены на рисунке.

252

ГЛАВА 9. ЗАДАЧИМНОГОКРИТЕРИАЛЬНОЙОПТИМИЗАЦИИ ВЭКОНОМИКЕ

§ 9.1. ПОСТАНОВКА ЗАДАЧИ МНОГОКРИТЕРИАЛЬНОЙ ОПТИМИЗАЦИИ

Задачи многокритериальной (или векторной) оптимизации возни-

кают в тех случаях, когда имеется несколько целей, которые не могут быть отражены одним критерием (например, стоимость, надежность и т. п.). Требуется найти точку области допустимых решений, которая минимизирует или максимизирует все эти критерии. Обозначим i-й частный критерий через zi (x) , а область допустимых решений через Q. Учтем, что изменением знака функции всегда можно свести задачу минимизации к задаче максимизации, и наоборот, мы можем сформулировать кратко задачу векторной оптимизации следующим образом:

Выбирая работу, человек, как правило, руководствуется несколькими критериями. Например, кому-то хочется, чтобы одновременно выполнялись такие условия:

∙заработная плата была как можно выше;

∙условия работы были как можно комфортнее;

∙место работы было как можно ближе к дому.

Другим примером задачи с многими критериями является модернизация производства, в процессе которой хочется достигнуть максимального роста эффективности с наименьшими затратами.

Еще один пример — выбор инвестиционного решения, когда хочется получить максимальный доход (или доходность) при наименьшем риске.

253

Конечно, решения, которое одновременно удовлетворяло бы всем противоречивым требованиям, как правило, не существует. Но математика может помочь и при решении таких задач. Помощь эта состоит не в нахождении несуществующего решения, одновременно обращающего все критерии в максимум, а в отбрасывании заведомо плохих решений.

§ 9.2. ОПТИМАЛЬНОСТЬПО ПАРЕТО

В идеальном случае в задаче (9.1.1)—(9.1.2) можно вести поиск такого решения, которое принадлежит пересечению множеств оптимальных решений всех однокритериальных задач. Но указанное пересечение обычно оказывается пустым множеством, и потому приходится рассматривать переговорное множество — множество допустимых решений [т. е. удовлетворяющих требованию (9.1.2)], оптимальных по Парето.

Изучение понятия оптимальности по Парето начнем с частного случая двух критериев.

Обозначим буквой E некоторую обобщенную характеристику произвольной инвестиционной операции, которую назовем эффективностью операции (в качестве E можно взять доход, доходность в процентах от вложенной суммы, доходность в процентах годовых, внутреннюю норму доходности и т. п.). Часто невозможно заранее точно предсказать эффективность той или иной операции, и такие операции рассматривают как с л у ч а й н ы е в е л и ч и н ы. При этом в качестве ожидаемой эффектив-

реальных значений эффективности инвестиционной операции от прогнозируемой эффективности (как в меньшую сторону, так и в бόльшую).

Если E — случайная эффективность инвестиционной операции, и в качестве ожидаемой эффективности операции мы выбрали математическое ожидание ME случайной величины E, то в качестве меры риска операции

отклонений случайных величин довольно-таки важно при анализе группы случайных величин, оно помогает выбрать из множества случайных величин оптимальные по Парето, отбросив заведомо «плохие».

Пусть на финансовом рынке существует возможность осуществить несколько инвестиционных операций, ожидаемые эффективности и риски которых известны и равны соответственно ME1, ME2, …, MEn и σ1, σ2, …, σn.

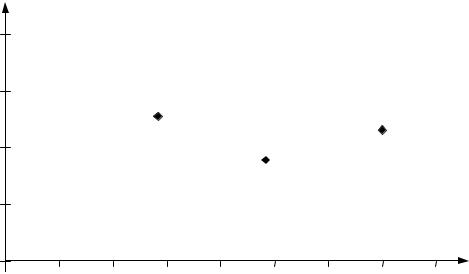
Говорят, что i-я операция доминирует j-ю, если

254

Операция называется оптимальной по Парето, если не существует операций, которые бы ее доминировали.

ПРИМЕР 9.2.1. Инвестор рассматривает четыре инвестиционные операции со случайными эффективностями, описываемыми случайными величинами E1, E2, E3, E4 с рядами распределения

Требуется определить, какие из этих операций оптимальны по Парето. Решение. Ожидаемые эффективности и риски равны соответственно

ME1 = 4,81, σ1 = 1,77, ME2 = 4,16, σ2 = 3,57, ME3 = 7,00, σ3 = 2,30,

ME4 = 2,81, σ4 = 2,54. Нанесем точки (MEi; σi) на единый график (рис. 9.2.1). i-я операция доминирует j-ю, если точка, соответствующая i-й операции, находится на графике правее и ниже точки, соответствующей j-й операции.

Видно, что первая операция доминирует вторую и четвертую, третья операция также доминирует вторую и четвертую. При этом первая операция не доминирует третью, а третья не доминирует первую. Первая и третья операции, таким образом, оптимальны по Парето.

σi

4

2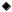

3

4

3

2

1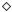

1

MEi

Рис. 9.2.1. График «риск — доходность»

255

Отметим, что операции, оптимальные по Парето, не обязательно являются «самыми лучшими» (и даже просто «хорошими») — эти операции н е я в л я ю т с я х у д ш и м и. Выбор операций среди оптимальных по Парето осуществляется на основе склонности лица, принимающего соответствующее решение, к риску.

В некоторых ситуациях предпочтительной оказывается операция, в которой ожидаемая эффективность вообще отрицательна. Например, если перед нами стоит выбор из двух операций:

∙потерять 1 руб.;

∙с вероятностью 0,5 получить 1 000 000 руб. и с вероятностью 0,5 потерять 100 000 руб.,

то обе эти операции окажутся оптимальными по Парето (ME1 = –1, σ1 = 0, ME2 = 450 000, σ2 = 450 000), но, скорее всего, мы склонимся к выбору первой операции, несмотря на то, что ожидаемый доход по ней составляет отрицательное число (–1 руб.), тогда как ожидаемый доход от исполнения второй операции составляет 450 000 руб. — слишком велик риск у второй операции, слишком велика вероятность больших потерь.

Рассмотренный подход может быть применен при анализе любых других задач многокритериальной оптимизации.

В произвольной задаче выбора наилучшей альтернативы по нескольким критериям (9.1.1)—(9.1.2) решение x(1) Q доминирует решение x( 2 ) Q , если x (1) по каждому из критериев не х уже x( 2) и хотя бы

∙существует такой критерий j, что z j (x(1) ) > z j (x(2) ) .i i

Решение x Q называется оптимальным по Парето, если не существует решений, которые бы его доминировали.

ПРИМЕР 9.2.2. Дана задача многокритериальной оптимизации:

Требуется найти множество решений, оптимальных по Парето. Решение. Очевидно, в данной задаче множество Парето совпадает с

областью допустимых решений [т. е. точек, удовлетворяющих условиям (9.2.1), они соответствуют пятиугольнику ABCDE на рис. 9.2.1, а].

Действительно, возьмем любую точку множества допустимых решений. Если мы от нее сдвинемся вправо, то значения критериев z2 и z3 увели-

256

чатся, но значение критерия z1 уменьшится. Если мы сдвинемся левее, то значения критериев z2 и z3 уменьшатся, но значение критерия z1 увеличится. Если мы сдвинемся ниже, то значения критериев z1 и z2 увеличатся, но значение критерия z3 уменьшится. Если мы сдвинемся выше, то значения критериев z1 и z2 уменьшатся, но значение критерия z3 увеличится.

Рис. 9.2.2. Переговорное множество, совпадающее с множеством допустимых решений

Таким образом, ни одна из точек множества допустимых решений не доминируется другими, т. е. все допустимые точки оптимальны по Парето. Рис. 9.2.3 иллюстрирует типичные варианты того, как выглядит множество Парето в случае выпуклого и невыпуклого множества допусти-

мых решений (оптимальные по Парето решения выделены жирным).

Рис. 9.2.3. Варианты конфигурации множества Парето

257

§ 9.3. СУБОПТИМИЗАЦИЯ

Выбор конкретного решения из переговорного множества — множества допустимых решений, оптимальных по Парето, предоставляется человеку — л и ц у, п р и н и м а ю щ е м у р е ш е н и е (и несущему за него ответственность).

Однако часто переговорное множество оказывается чересчур громоздким и проанализировать все возможные варианты за разумное время невозможно.

В таких ситуациях пользуются некоторыми специальными приемами, сужающими множество Парето (в идеале — до одного решения).

Субоптимизация состоит в том, что выделяется один максимизируемый критерий (с номером k), а для остальных критериев (с номерами i ¹ k ) задаются нижние границы γi :

zk (x) ® max, x ÎQ,

zi (x) gi , i =1, 2, …, k -1, k +1, m.

ПРИМЕР 9.3.1. Требуется решить задачу многокритериальной оптимизации из примера 9.2.2 методом субоптимизации, приняв первый критерий за основной, а для второго и третьего критерия задав нижние границы равными γ2 = 4 и γ3 = −8 .

Решение. Задача, полученная из исходной путем добавления по второму и третьему критериям ограничений снизу, имеет следующий вид:

z1 = −x1 + 2x2 → max ,

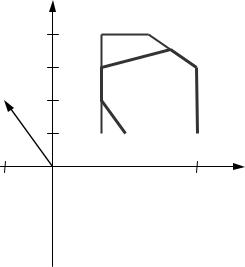
Градиент целевой функции и множество допустимых решений этой задачи представлены на рис. 9.3.1, из которого очевидно, что

суб. = 1 x .

3

При этом

z1 = 5, z2 = 5, z3 = −8.

258

x2

AB

2

1E D

Рис. 9.3.1. Субоптимизация

§ 9.4. ЛЕКСИКОГРАФИЧЕСКАЯОПТИМИЗАЦИЯ

Лексикографическая оптимизация предполагает, что критерии упорядочены по относительной важности. На первом шаге из множества Парето выделяются решения, имеющие максимальную оценку по важнейшему критерию, и если такое решение единственно, оно считается оптимальным. Если же таких решений не одно, то среди них отбирают те, которые имеют максимальную оценку по следующему критерию, и т. д.

ПРИМЕР 9.4.1. Требуется решить задачу из примера 9.2.2 методом лексикографической оптимизации.

Решение. Из рис. 9.2.2 очевидно, что решение, имеющее максимальную оценку по первому критерию, единственно и находится в точке A, т. е.

лекс. = 1

x .4

При этом

z1 = 7, z2 = 6, z3 = −11.

§ 9.5. СВЕРТКА КРИТЕРИЕВ

Метод обобщенного критерия предлагает перейти от m частных критериев к так называемой свертке критериев:

m

w= ∑αi zi (x) → max,

i=1

xQ,

где веса α i определяют важность критериев.

259

w= 0,5z1 + 0, 25z2 + 0, 25z3 =

=0,5(−x1 + 2x2 ) + 0, 25(2x1 + x2 ) + 0, 25( x1 − 3x2 ) = 0, 25( x1 + 2x2 )

на множестве допустимых решений

x + x 6,

1 2

1 x1 3,

1 x2 4

достигается, как видно из рис. 9.2.2, в точке B:

Рис. 9.5.1. Свертка критериев

При этом

z1 = 6, z2 = 8, z3 = −16.

§ 9.6. МЕТОД ИДЕАЛЬНОЙТОЧКИ

Метод идеальной точки состоит в поиске решения х из множества Парето, для которого значения критериев как можно меньше отклоняются от своих оптимальных значений. Иными словами, от задачи (9.1.1)—(9.1.2)

переходят к задаче

260