Алгоритм венгерского метода решения задач о назначениях [8]

Предварительный этап.

Шаг 1. При максимизации целевой функции (суммы показателей эффективности назначений) в каждом столбце матрицы С найти максимальный элемент и каждый элемент этого столбца вычесть из максимального. При минимизации целевой функции (суммы показателей эффективности назначений) в каждом столбце матрицы С найти минимальный элемент и вычесть его из каждого элемента этого столбца.

В результате образуется матрица С с неотрицательными элементами. В каждом столбце матрицы С имеется, по крайней мере, один нуль.

Шаг 2. В каждой строке матрицы С найти минимальный элемент и вычесть его из каждого элемента этой строки.

В результате образуется матрица С₀ с неотрицательными элементами. В каждом столбце и каждой строке матрицы С₀ имеется, по крайней мере, по одному нулю.

Шаг 3. Отме­тить произвольный нуль в первом столбце звездочкой. Начиная со второго столбца просматривать каждый столбец матрицы С₀ и отмечать в нем звездочкой нуль, расположенный в строке, где нет нуля со звездочкой. В каждом столбце можно отметить звездочкой только один нуль. Очевидно, что нули матрицы С₀, отмеченные звездочкой, являются по построению независимыми. На этом предварительный этап заканчи­вается.

(k + 1)-я итерация. Допустим, что k-я итерация уже проведена и в результате получена матрица С_k. Если в матрице С_k имеется ровно п нулей со звездочкой, то процесс решения заканчивается. Если же число нулей со звездочкой меньше п, то переходим к (k + 1)-й ите­рации.

Каждая итерация начинается первым и заканчивается вторым эта­пом. Между ними может несколько раз проводиться пара этапов: третий – первый. Перед началом итерации знаком «+» выделяют столбцы матрицы С_k, которые содержат нули со звездочкой.

Первый этап. Просмотреть невыделенные столбцы матри­цы С_k. Если среди них не окажется нулевых элементов, то перейти к третьему этапу.

Если же невыделенный нуль матрицы С_k обнаружен, то возможен один из двух случаев:

1. строка, содержащая невыделенный нуль, содержит также и нуль со звездочкой;

2. эта строка не содержит нуля со звездочкой.

В первом случае невыделенный нуль отметить штрихом и выделить строку, в которой он содержится, постановкой справа от нее зна­ка «+». Затем уничтожить знак «+», обводя его кружком над тем столбцом, на пересечении которого с данной выделенной строкой со­держится нуль со звездочкой.

Далее просмотреть этот столбец, отыскивая в нем невыделен­ный нуль (нули), не отмеченный звездочкой.

 Если такой нуль найден и он единственный в столбце, то отметить его штрихом и выделить строку (строки), содержащую такой нуль (нули), знаком «+». Затем просмотреть эту строку (строки), отыскивая в них нуль со звез­дочкой.

 Если такой нуль в столбце найден, но он не единственный в столбце, то из этих нулей следует выбрать:

• в первую очередь такой нуль, в одной строке с которым, нет 0*;

• во вторую очередь такой нуль, в одной строке с которым имеется 0*, но в одном столбце с этим 0* имеется невыделенный нуль;

• в последнюю очередь такой нуль, в одной строке с которым имеется 0*, но в одном столбце с этим 0* отсутствует невыделенный нуль;

Этот процесс за конечное число шагов заканчивается одним из следующих исходов:

Исход 1. Все нули матрицы С_k выделены, т. е. находятся в выделенных строках или столбцах. В этом случае перейти к третьему этапу;

Исход 2. Имеется невыделенный нуль в строке, где нет нуля со звездочкой. Тогда перейти ко второму этапу, отметив последний по порядку нуль штрихом.

Во втором случае, отметив невыделенный нуль штрихом, сразу переходят ко второму этапу.

Второй этап. Построить следующую цепочку из элементов матрицы С_k: исходный нуль со штрихом, нуль со звездочкой, располо­женный в одном столбце с первым, нуль со штрихом, расположенный в одной строке с предшествующим нулем со звездочкой, и т. д. Итак, цепочка образуется передвижением от 0' к 0* по столбцу, от 0* к 0' по строке и т. д.

Можно доказать, что описанный алгоритм построения цепочки однозначен и конечен. При этом цепочка всегда начинается и закан­чивается нулем со штрихом. Далее над элементами цепочки, стоящими на нечетных местах (0'), поставить звездочки, уничтожая их над четными элементами (0*). Затем уничтожить все штрихи над элементами мат­рицы С_k и знаки «+». При этом количество независимых нулей будет увеличено на единицу. (k + 1)-я итерация закончена.

Третий этап. К этому этапу следует переходить после первого этапа в случае, если все нули матрицы С_k выделены, т. е. находятся в выделенных строках или столбцах. В таком случае среди невыделенных элементов матрицы С_k выбрать минимальный элемент и обозначить его h > 0.

Далее следует:

• вычесть h из всех элементов матрицы С_k, расположенных в невыделенных стро­ках, и

• прибавить h ко всем элементам матрицы С_k, расположенным в выделенных столбцах.

В результате получается новая матрица , эквивалентнаяС_k.

Поскольку среди невыделенных элементов матрицы появятся новые нули (согласно определению), следует перейти к первому этапу, а вместо матрицыС_k рассматривать матрицу .

Завершив первый этап либо перейти ко второму этапу, если невыделенный нуль находится в строке, которая не содержит нуля со звездочкой, либо вновь возвратиться к третье­му этапу, если в результате выполнения первого этапа все нули матрицы окажутся выделенными.

• В первом случае после проведения второго этапа итерация закан­чивается.

• Во втором случае после проведения третьего этапа получается матрица ~~С_k. В матрице появятся невыделенные нули, и всю последовательность операций, начиная с первого этапа, надо повторить.После конечного числа повторений очередной первый этап обязательно закончится переходом на второй этап, при выполнении которого количество независимых нулей увеличится на единицу, а после выполнения которого (k + 1)-я итерация за­канчивается.

Пример 9. Решим венгерским методом задачу:

На боевом надводном корабле имеется 5 зенитных огневых средств (ЗОС). На корабль совершается одновременный налет авиации противника в количестве 5 единиц. Поражающий потенциал каждого i–го ЗОС по j–му летательному аппарату противника равен (количество потенциально уничтожаемыхj–х летательных аппаратов за время атаки НК одним ЛА). Предполагается, что любое ЗОС может обстрелять любую цель.

Распределить ЗОС по ВЦ таким образом, чтобы суммарный поражающий потенциал был максимален, при условиях:

• на одну ВЦ может быть назначено только одно ЗОС;

• все цели должны быть обстреляны ЗОС.

Решение:

Предварительный этап.



+ + +

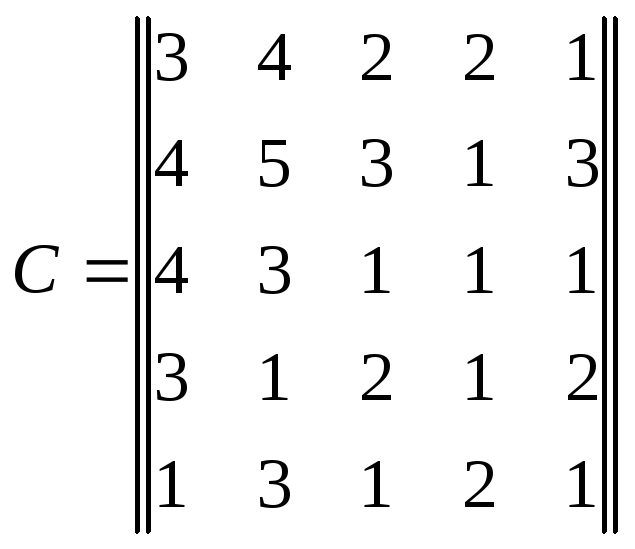
Первая итерация.

Первый этап.

+ +

+ + +

+

+



В

+ +

+

+

торой этап.



Вторая итерация.

П

+ +

+ + + +

+

+

ервый этап.



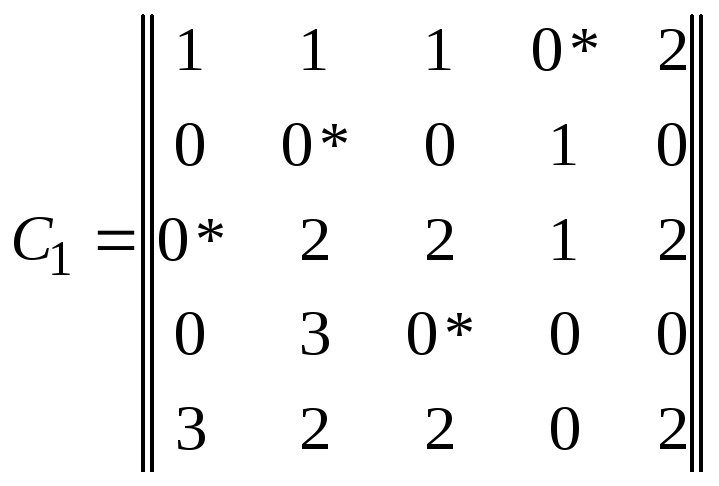
Поскольку все нули матрицы С₁ выделены следует перейти к третьему этапу.

Т

+

+

ретий этап.

+ +

+ +

+

+

+

+

h =1 

П

+

+

+

+

ервый этап.



Второй этап.



В результате решения задачи о назначениях венгерским методом получили, что последовательность =4,=4,=3,=2,=2 дает максимальное значение целевой функции=15. Из этого следует, что для отражения атаки СВН противника наиболее эффективным будет следующий вариант назначения ЗОС на ВЦ:

ЗОС	3	1	2	4	5
ВЦ	1	2	3	5	4

Упражнения.

1. Найти опорный план транспортной задачи методами «Северо-западного угла», «Наименьшей стоимости», «Фогеля»:

ПН ПО	B1	B2	B3	B4	B5	Запасы ai
A1	10	8	5	6	9	48
A2	6	7	8	6	5	30
A3	8	7	8	6	5	27
A4	7	5	4	6	8	20
Заявки bj	18	27	42	12	26	125

2. Решить транспортную задачу из задания 1 распределительным методом.

3. Решить транспортную задачу из задания 1 методом потенциалов.

4. Венгерским методом решить задачу назначения при поиске максимума:

5. Венгерским методом решить задачу назначения при поиске минимума:

Контрольные вопросы:

1. Дайте формулировку транспортной задачи линейного программирования.

2. Чем отличается сбалансированная транспортная задача от не сбалансированной транспортной задачи?

3. Сколько в сбалансированной транспортной задаче должно быть базисных переменных?

4. Дайте определение понятиям: план, допустимый план, опорный допустимый план, оптимальный план, используемым при решении транспортной задачи.

5. Сформулируйте алгоритм нахождения опорного плана методом северо-западного угла.

6. Сформулируйте алгоритм нахождения опорного плана методом наименьшей стоимости.

7. Сформулируйте алгоритм нахождения опорного плана методом Фогеля.

8. Сформулируйте алгоритм нахождения оптимального плана распределительным методом.

9. Сформулируйте алгоритм нахождения оптимального плана методом потенциалов.

10. Дайте формулировку задачи о назначениях.

11. Каким образом в задаче о назначениях при разных количествах объектов и средств формируется квадратная матрица назначений?

12. Сформулируйте алгоритм решения задачи о назначениях Венгерским методом.

13. Каким образом на предварительном этапе формируется исходная матрица назначений при максимизации целевой функции?

14. Каким образом на предварительном этапе формируется исходная матрица назначений при минимизации целевой функции?

15. В чем заключается суть первого этапа решения задачи о назначениях Венгерским методом?

16. В чем заключается суть второго этапа решения задачи о назначениях Венгерским методом?

17. В чем заключается суть третьего этапа решения задачи о назначениях Венгерским методом?

18. Сколько первых, вторых и третьих этапов может находиться в одной итерации решения задачи о назначениях Венгерским методом? Какова последовательность выполнения этапов в итерации?

19. Сколько независимых нулей должно быть в матрице назначений для принятия решения о том, что оптимальное назначение средств на объекты найдено?