Понятие модели назначения. Разновидности моделей назначения.

Мы изучили два метода решения транспортной задачи линейного программирования: распределительный метод и метод потенциалов. В области военного планирования такими методами решаются задачи:

• определения оптимального плана военных перевозок;

• наиболее выгодного расположения складов и объектов;

• распределения сил и средств по объектам противника для нанесения ударов.

Последняя из этих задач несколько отличается от остальных тем, что количество назначений может быть либо 0, либо 1 (т. е. либо средство назначено на цель, либо нет). Это означает, что одно средство может обслуживать только один объект.

Постановка задачи о назначениях

Если количество средств и объектов одинаково, то каждый объект должен быть обслужен. Но эффект от обслуживания одного и того же объекта различными средствами различен. Эффективность обслуживания j-го объекта i-м средством есть коэффициент c_ij перед переменной задачи , а количество назначенийi-го средства на обслуживание j-го объекта может быть равно либо 0, либо 1. Эффективности всех возможных назначений сведены в матрицу назначений.

.

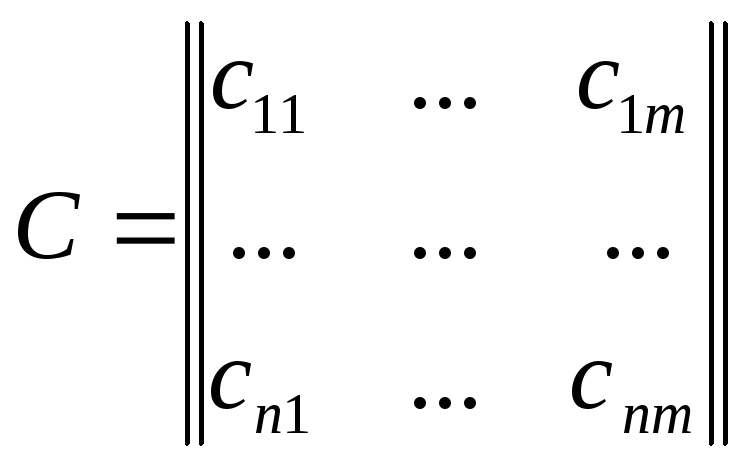Если количество средств и объектов одинаково, то матрица назначений будет квадратной. Эффективности всех возможных назначений также можно записать и в транспортную таблицу.

ПН ПО	B1	B2	…	Bm	Запасы ai
A1	c11	c12	…	c1m	1
A2	c21	c22	…	c2m	1
…	…	…	…	…	…
An	cn1	cn2	…	cnm	1
Заявки bj	1	1	…	1	n = m

Суммарная эффективность назначений всех средств на все объекты должна быть оптимальной, т. е. значение интегрального показателя эффективности должно быть оптимальным.

Например, если показателем эффективности является вероятность поражения нашего корабля или количество наших затрат (потерь) при назначении средства на объект, то его значение должно быть минимальным. Если же показателем эффективности является, например, математическое ожидание количества уничтоженных средств воздушного нападения противника или количество наших доходов (выигрышей) при назначении средства на объект, то его значение должно быть максимальным.

В результате решения задачи о назначениях требуется выбрать такую последовательность ,, …,, чтобы

• целевая функция: сумма была максимальна или минимальна и при этом выполнялись

• ограничения: из каждой строки или столбца матрицы С был выбран только один элемент.

Здесь i – номер строки матрицы С, а - эффективность назначенияi-го средства на обслуживание j-го объекта, единственного назначения, выбранного из всех возможных назначений для i-го средства.

Разновидности моделей назначения [8]

Существуют три разновидности моделей назначения:

• количество средств (работников) и объектов (работ) одинаково n = m;

• количество средств (работников) больше, чем объектов (работ) n > m;

• количество средств (работников) меньше, чем объектов (работ) n < m.

Первая разновидность соответствует классической постановке задачи о назначениях с квадратной матрицей эффективности каждого возможного назначения.

Вторая разновидность модели назначения сводится к первой (матрица С сводится к квадратной) путем добавления фиктивных объектов (столбцов). Третья разновидность модели назначения сводится к первой (матрица С сводится к квадратной) путем добавления фиктивных средств (строк). В этих случаях на пересечении фиктивного столбца (строки) с другими строками (столбцами) проставляется значение эффективности данного назначения: = 0, если требуется максимизировать целевую функцию, и=, если требуется минимизировать целевую функцию.

Решение транспортной задачи линейного программирования

о назначениях Венгерским методом [8]

Задачу о назначениях можно эффективно решить точно так же, как и транспортную задачу. Вместе с тем тот факт, что все величины спроса и предложений равны 1, привел к разработке упрошенного алгоритма решения, названного венгерским методом. Этот метод был впервые предложен венгерским математиком Эгервари в 1931 году. В 1953 году математик Г. Кун перевел работу Эгервари на английский язык, развил и усовершенствовал метод. Хотя этот метод не имеет никакого отношения к транспортной задаче, он, как и метод потенциалов, все равно основан на симплекс-методе.

Прежде чем приступить к описанию алгоритма венгерского метода введем три понятия:

• Нулевой элемент матрицы С называется независимым нулём, если строка и столбец, на пересечении которых расположен этот элемент, не содержат других нулей.

• Две прямоугольные матрицы С и С называются эквивалентными, если c_ij = c_ij + _i + _j для всех i, j, где _i – величина (константа), на которую изменяются значения всех элементов строки i, а _j – величина (константа), на которую изменяются значения всех элементов столбца j. Задачи выбора, определяемые эквивалентными матрицами, являются эквивалентными.

• Элементы, расположенные в выделенных строках или столбцах, называются выделенными элементами.

Алгоритм венгерского метода состоит из предварительного этапа и не более чем (n – 2) последовательно про­водимых итераций. Здесь n равно количеству строк и равно количеству столбцов квадратной матрицы. Каждая итерация связана с эквивалентными пре­образованиями матрицы, полученной в результате проведения преды­дущей итерации, и с выбором максимального числа независимых нулей. Окончательным результатом итерации является увеличение чис­ла независимых нулей на единицу.

Как только количество независимых нулей станет равным n, проб­лема выбора оказывается решенной, а оптимальный вариант опреде­ляется позициями независимых нулей в последней матрице.