67

4.3. Методы решения транспортной задачи

линейного программирования

___________________________________________________________________________________________________________

4.3. Методы решения транспортной задачи

линейного программирования

Постановка транспортной задачи линейного программирования

Имеется n складов и m пунктов потребления. На складах имеются запасы однотипного товара a₁, …, a_n. Пункты потребления подали заявки на количество товара b₁, …, b_m. Сумма заявок не превосходит суммы запасов (т. е. все заявки могут и должны быть выполнены). Стоимость перевозки единицы товара соi-го склада в j-й пункт равна c_ij.

Требуется составить такой план перевозок при котором все заявки были бы удовлетворены, и при этом общая стоимость всех перевозок была минимальной. Т. е. нужно определить с какого склада, в какой пункт потребления и сколько единиц товара следует перевезти, чтобы суммарная стоимость всех перевозок была минимальной при условиях, что со склада нельзя вывести товара больше, чем имеется на складе, и что все заявки пунктов потребления будут выполнены [1].

Если предположить, что , то транспортная задача называетсясбалансированной, а в противном случае – не сбалансированной транспортной задачей.

Для того чтобы не сбалансированную транспортную задачу сделать сбалансированной, следует ввести фиктивные пункты назначения (если ) или отправления (если). Количество единиц товара, которое нужно вывезти из фиктивного пункта отправления в реальный пункт назначения говорит о том, что заявка этого пункта будет недовыполнена на это количество. Количество единиц товара, которое нужно вывезти из реального пункта отправления в фиктивный пункт назначения говорит о том, что после окончания перевозок в этом пункте останется именно это количество товара.

Выполнение баланса транспортной задачи необходимо для того, чтобы иметь возможность применить алгоритм решения, построенный на использовании транспортных таблиц.

Для сбалансированной транспортной задачи можно сформулировать целевую функцию, которую необходимо минимизировать:

при ограничениях 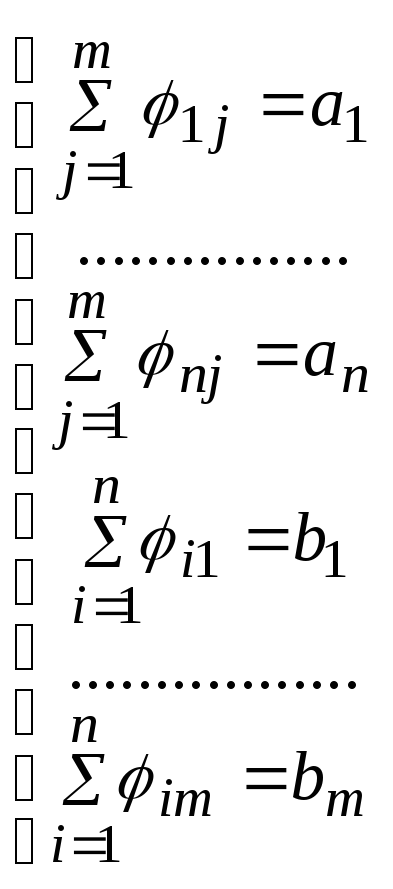и_ij  0, ,

где первая группа ограничений показывает, что количество единиц вывозимого со склада товара равно количеству единиц товара, имеющегося на складе, а вторая – что все заявки пунктов потребления должны быть выполнены.

Основные свойства транспортной задачи

линейного программирования

Поскольку в сбалансированной транспортной задаче то при сложении всех уравнений первой и второй группы мы получим одно и то же значение суммы. Это означает, что независимыми являются неm+n, а m+n-1 уравнений (т. е. одно из уравнений является избыточным). Следовательно, в транспортной задаче количество базисных переменных: а небазисных:[19].

Определения:

План перевозок (план) – это любая совокупность значений .

Допустимый план перевозок – это план перевозок, который удовлетворяет балансовым условиям: все заявки удовлетворены – все запасы исчерпаны.

Опорный допустимый план перевозок – это допустимый план перевозок, в котором отличны от нуля не более перевозок, а остальные перевозки равны нулю.

Оптимальный план перевозок – это допустимый план перевозок, который приводит к минимальной стоимости всех перевозок.

Методы решения транспортной задачи сводятся к операциям с транспортной таблицей:

ПН ПО	B1	B2	…	Bm	Запасы ai
A1	c11	c12	…	c1m	a1
A2	c21	c22	…	c2m	a2
…	…	…	…	…	…
An	cn1	cn2	…	cnm	an
Заявки bj	b1	b2	…	bm

Клетки таблицы, в которые будем записывать отличные от нуля перевозки, назовем базисными, а остальные клетки – свободными.

Решение транспортной задачи заключается в нахождении таких положительных значений перевозок, которые, будучи поставлены в базисных клетках транспортной таблицы, удовлетворяли бы следующим условиям:

• сумма перевозок в каждой строке должна быть равна запасам данного пункта отправления (ПО);

• сумма перевозок в каждой столбце должна быть равна заявке данного пункта назначения (ПН);

• общая стоимость перевозок минимальна.

Методы нахождения опорного плана транспортной задачи

линейного программирования [19]

Для построения начального решения транспортной задачи применяются следующие методы:

1. метод северо-западного угла;

2. метод наименьшей стоимости (метод минимального элемента);

3. метод Фогеля.

Различие этих методов заключается в «качестве начального решения», т. е. насколько начальное решение ближе к оптимальному решению. В общем случае метод Фогеля дает наилучшее решение, а метод северо-западного угла – наихудшее. Однако метод северо-западного угла требует меньшего объема вычислений.

 Самым простым методом нахождения опорного допустимого плана перевозок является метод северо-западного угла. Заполнение транспортной таблицы, в соответствии с этим методом, начинается с самой левой верхней ячейки, т. е. с переменной .