1 2 4 5

.

Тогда новая нижняя граница равна = =11 + 1+1=13.

Проставим это значение оценки нижней границы вершине (5, 3) в дереве поиска.

Ш

1 2 4 5

аг 5. Выбор дуги, разбивающей множество гамильтоновых контуров, содержащему дугу (5, 3), на два подмножества.

.

Выберем дуги (i, j), для которых в матрице Т₁ t_ij1 = 0. Для каждого такого нуля в матрице Т₁ вычислим значения (i, j): (1, 2)=0, (1, 4)=0, (2, 1)=0, (2, 4)=0, (3, 1)=1, (4, 2)=0, (4, 5)=1.

Для разбиения множества, уже содержащего дугу (5, 3), на два подмножества можно выбрать одну из двух дуг: (3, 1) и (4, 5). Выберем, например, дугу (3, 1).

Оценка нижней границы времени передачи сообщения по оптимальному маршруту при отсутствии дуги (3, 1) в маршруте изменится и будет равна W_н2 = 13+1=14.

В бинарое дерево поиска (рис. 5) на третьем уровне должны быть включены две вершины: вершина сW_н2 = 14 и вершина (3, 1). Поскольку подмножество гамильтоновых контуров, не содержащих дугу (3, 1), имеет нижнюю границу W_н2 = 14, более всего превышающую нижнюю границу подмножества гамильтоновых контуров, содержащих дугу (5, 3), W_н1 = 13, то подмножество, соответствующее вершине исключается из рассмотрения как не перспективное. Следовательно, необходимо просмотреть подмножество гамильтоновых контуров, обязательно содержащих дуги (5, 3) и (3, 1).

Шаг 6. Определение матрицы Т₂, соответствующей подмножеству гамильтоновых контуров, обязательно содержащих дуги (5, 3) и (3, 1).

Преобразуем матрицу Т₁ в матрицу Т₂ путем вычеркивания из матрицы Т₁ 3-й строки и 1-го столбца. Замену значения элемента (1, 3) на  производить не будем, т. к. в матрице уже нет третьего столбца и значит элемент (1, 3) отсутствует.

1 2 4 5

2 4 5



Шаг 7. Определение нижней границы времени передачи сообщения по маршруту, обязательно содержащему дуги (5, 3) и (3, 1).

Для определения новой нижней границы приведем матрицу Т₂ по строкам и по столбцам. Поскольку в каждой строке и в каждом столбце этой матрицы находятся нулевые элементы, то матрицы Т₂, Т₂ и Т₂ совпадают. Следовательно, оценка нижней границы времени передачи сообщения по оптимальному маршруту, содержащему дуги (5, 3) и (3, 1) в маршруте не изменится и будет равна W_н2 = 13. Проставим это значение оценки нижней границы вершине (3, 1) в дереве поиска.

Ш

2 4 5

аг 8. Выбор дуги, разбивающей множество гамильтоновых контуров, содержащих дуги (5, 3) и (3, 1), на два подмножества.

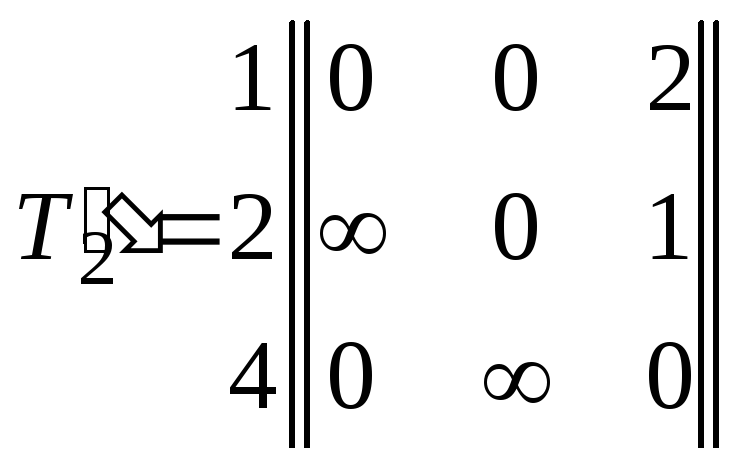
Выберем дуги (i, j), для которых в матрице Т₂ t_ij2 = 0. Для каждого такого нуля в матрице Т₂ вычислим значения (i, j): (1, 2)=0, (1, 4)=0, (2, 4)=1, (4, 2)=0, (4, 5)=1.

Для разбиения множества, уже содержащего дуги (5, 3) и (3, 1), на два подмножества можно выбрать одну из двух дуг: (2, 4) и (4, 5). Выберем, например, дугу (2, 4).

Оценка нижней границы времени передачи сообщения по оптимальному маршруту при отсутствии дуги (2, 4) в маршруте изменится и будет равна W_н3 = 13+1=14.

В бинарое дерево поиска (рис. 4.5.5) на третьем уровне должны быть включены две вершины: вершина сW_н3 = 14 и вершина (2, 4). Поскольку подмножество гамильтоновых контуров, не содержащих дугу (2, 4), имеет нижнюю границу W_н3 = 14, более всего превышающую нижнюю границу подмножества гамильтоновых контуров, содержащих дуги (5, 3) и (3, 1), W_н2 = 13, то подмножество, соответствующее вершине исключается из рассмотрения как не перспективное. Следовательно, необходимо просмотреть подмножество гамильтоновых контуров, обязательно содержащих дуги (5, 3), (3, 1) и (2, 4).

Шаг 9. Определение матрицы Т₃, соответствующей подмножеству гамильтоновых контуров, обязательно содержащих дуги (5, 3), (3, 1) и (2, 4).

П

2 5

2 4 5

реобразуем матрицуТ₂ в матрицу Т₃ путем вычеркивания из матрицы Т₂ 2-й строки и 4-го столбца, заменяя значение элемента (4, 2) на : t₄₂ = .



Шаг 10. Определение нижней границы времени передачи сообщения по маршруту, обязательно содержащему дуги (5, 3), (3, 1) и (2, 4).

Для определения новой нижней границы приведем матрицу Т₃ по строкам и по столбцам. Поскольку в каждой строке и в каждом столбце этой матрицы находятся нулевые элементы, то матрицы Т₃, Т₃ и Т₃ совпадают. Следовательно, оценка нижней границы времени передачи сообщения по оптимальному маршруту, содержащему дуги (5, 3), (3, 1) и (2, 4) в маршруте не изменится и будет равна W_н3 = 13. Проставим это значение оценки нижней границы вершине (2, 4) в дереве поиска.

Ш

2 5

аг 11. Выбор дуги, разбивающей множество гамильтоновых контуров, содержащих дуги (5, 3) , (3, 1) и (2, 4), на два подмножества.

Выберем дуги (i, j), для которых в матрице Т₃ t_ij3 = 0. Для каждого такого нуля в матрице Т₃ вычислим значения (i, j): (1, 2)=, (4, 5)= .

Значения «» для (1, 2) и (4, 5) свидетельствуют о том, что если при уже выбранных дугах (5, 3), (3, 1) и (2, 4) не выбрать в маршрут дуги (1, 2) и (4, 5), то гамильтонов контур не получится, т.е. маршрут, удовлетворяющий требованиям задачи, не будет построен.

Для разбиения множества, уже содержащего дуги (5, 3), (3, 1) и (2, 4), на два подмножества можно выбрать одну из двух дуг: (1, 2) и (4, 5). Выберем, например, дугу (4, 5).

Оценка нижней границы времени передачи сообщения по оптимальному маршруту при отсутствии дуги (4, 5) в маршруте изменится и будет равна W_н4 = 13+ =.

В бинарое дерево поиска (рис. 4.5.5) на четвертом уровне должны быть включены две вершины: вершина сW_н4= и вершина (4, 5). Поскольку подмножество гамильтоновых контуров, не содержащих дугу (4, 5), имеет нижнюю границу W_н4=, более всего превышающую нижнюю границу подмножества гамильтоновых контуров, содержащих дуги (5, 3), (3, 1) и (2, 4), W_н3=13, то подмножество, соответствующее вершине исключается из рассмотрения как не перспективное. Следовательно, необходимо просмотреть подмножество гамильтоновых контуров, обязательно содержащих дуги (5, 3), (3, 1), (2, 4) и (4, 5).

Шаг 12. Определение матрицы Т₄, соответствующей подмножеству гамильтоновых контуров, обязательно содержащих дуги (5, 3), (3, 1), (2, 4) и (4, 5).

Преобразуем матрицу Т₃ в матрицу Т₄ путем вычеркивания из матрицы Т₃ 4-й строки и 5-го столбца. Заменять значение элемента (5, 4) на  не будем, поскольку в матрице Т₃ уже нет 5-й строки.

2 5

2



Шаг 13. Определение нижней границы времени передачи сообщения по маршруту, обязательно содержащему дуги (5, 3), (3, 1), (2, 4) и (4, 5).

Для определения новой нижней границы приведем матрицу Т₄ по строкам и по столбцам. Поскольку в каждой строке и в каждом столбце этой матрицы находятся нулевые элементы, то матрицы Т₄, Т₄ и Т₄ совпадают. Следовательно, оценка нижней границы времени передачи сообщения по оптимальному маршруту, содержащему дуги (5, 3), (3, 1), (2, 4) и (4, 5) в маршруте не изменится и будет равна W_н4 = 13. Проставим это значение оценки нижней границы вершине (4, 5) в дереве поиска.

Поскольку матрица Т₄ содержит всего один элемент (1, 2), то в бинарое дерево поиска (рис. 4.5.5) на пятом уровне должны быть включены две вершины: вершина сW_н5 =  (было вычислено на шаге 11) и вершина (1, 2) с W_н5 =13.

Поскольку подмножество гамильтоновых контуров, не содержащих дугу (1, 2), имеет нижнюю границу W_н5 = , более всего превышающую нижнюю границу подмножества гамильтоновых контуров, содержащих дуги (5,3), (3,1), (2,4) и (4,5), W_н4 = 13, то подмножество, соответствующее вершине исключается из рассмотрения как не перспективное.

Следовательно, оптимальный маршрут передачи сообщения об организации вычислительной сети на соединении надводных кораблей обязательно содержит дуги (5, 3), (3, 1), (2, 4), (4, 5) и (1, 2).

W_н = 11

+ (3, 5)=4

+ 2

(5,3)

W_н1 = 15

W_н1 = 13

+ (3, 1)=1

+ 0

(3,1)

W_н2 = 14

W_н2 = 13

+ 0

+ (2, 4)=1

(2,4)

W_н3 = 14

W_н3 = 13

+ 0

+ (4, 5)= 

(4,5)

W_н4 = 

W_н4 = 13

+ 0

+ (1, 2)= 

W_н5 = 13

(1,2)

W_н5 = 

Рис. 4.5.5. Бинарное дерево поиска оптимального маршрута Комивояжера

Ответ. Оптимальный маршрут передачи сообщения об организации вычислительной сети на соединении надводных кораблей будет выглядеть так: 124531. Время передачи сообщения по этому маршруту равно 13 секундам.

Упражнения:

1. Решить задачу ЦП методом Гомори.

Четверо рыбаков поймали какое-то количество рыбы, но вечером делить улов не стали, а легли спать. Причем договорились о том, что кто первым проснется, тот других будить не будет, а возьмет себе третью часть улова и уедет.

Утром первым проснулся один рыбак. Он разделил улов на четыре части, но одна рыбка осталась лишней. Рыбак выбросил ее в озеро (чтобы всем досталось поровну), забрал себе одну четвертую часть улова, остальную рыбу сложил в ведро для трех своих товарищей, и уехал.

Через час проснулся второй рыбак. Он, не зная, что первый рыбак уже взял свою часть улова, тоже разделил улов на четыре части, но одна рыбка опять осталась лишней. Рыбак выбросил ее в озеро (чтобы всем досталось поровну), забрал себе одну четвертую часть улова, остальную рыбу сложил в ведро для трех своих товарищей, и уехал.

Еще через час проснулся третий рыбак. Он, не зная, что двое его товарищей уже взяли свои части улова, тоже разделил улов на четыре части, но одна рыбка опять осталась лишней. Рыбак выбросил ее в озеро (чтобы всем досталось поровну), забрал себе одну четвертую часть улова, остальную рыбу сложил в ведро для трех своих товарищей, и уехал.

Наконец, еще через час проснулся четвертый рыбак. Он, не зная, что трое его товарищей уже взяли свои части улова, тоже разделил улов на четыре части, но одна рыбка опять осталась лишней. Рыбак выбросил ее в озеро (чтобы всем досталось поровну), забрал себе одну четвертую часть улова, остальную рыбу сложил в ведро для трех своих товарищей, и уехал.

Какое минимальное количество рыбы поймали четверо рыбаков?

2. Решить задачу ЦП методом ветвей и границ.

На соединении из 5 надводных кораблей существует вычислительная сеть обмена данными. Времена передачи сообщений между соседними узлами связи, установленными на кораблях, сведены в матрицу Т.

Определить маршрут передачи сообщения об организации вычислительной сети с флагманского корабля (корабль №1) на остальные корабли, чтобы время передачи сообщения было минимальным. ФК должен получить квитанцию от КС, который получит сообщение последним.

Контрольные вопросы:

1. Какими свойствами должны обладать значения целевой функции и ее аргументов в задаче целочисленного программирования?

2. В чем заключается суть решения задачи целочисленного программирования методом Гомори?

3. Каким образом при решении задачи целочисленного программирования методом Гомори вводится дополнительное линейное ограничение?

4. Как вычисляются значения и?

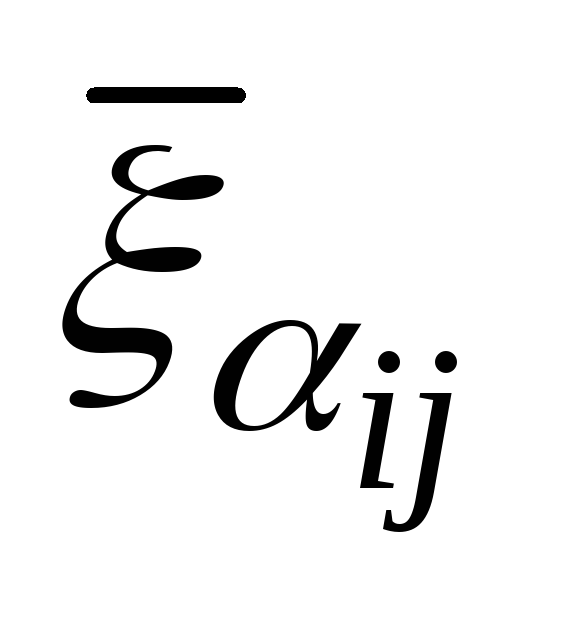5. Когда при решении задачи целочисленного программирования методом Гомори принимается решение о нахождении оптимальных значений целевой функции и ее аргументов?

6. В чем заключается суть решения задачи целочисленного программирования методом ветвей и границ?

7. Сформулируйте задачу Коммивояжера.

8. Дайте определение понятию Гамильтонов контур.

9. Как при решении задачи Коммивояжера методом ветвей и границ производится приведение матрицы расстояний по строкам и по столбцам?

10. Как определяется нижняя граница целевой функции в задаче Коммивояжера при ее решении методом ветвей и границ?

11. Как при решении задачи Коммивояжера методом ветвей и границ производится разбиение множества допустимых решений на два подмножества?

12. Как при решении задачи Коммивояжера методом ветвей и границ производится выбор отрезка маршрута, по которому производится разбиение множества допустимых решений на два подмножества?

13. Объясните, каким образом построено бинарное дерево поиска оптимального маршрута Комивояжера на рисунке 4.5.5.