1 2 3 4 5

Определить маршрут передачи сообщения об организации вычислительной сети с флагманского корабля (корабль №1) на остальные корабли, чтобы время передачи сообщения было минимальным. ФК должен получить квитанцию от КС, который получит сообщение последним.

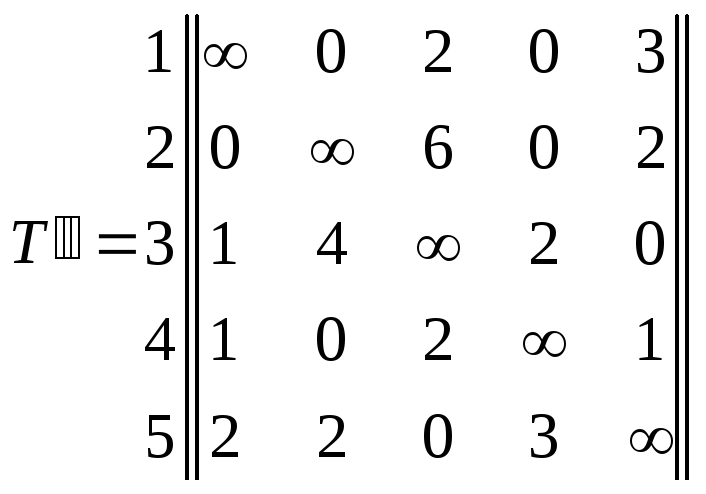
Решение. Рассмотрим граф, соответствующий возможным маршрутам передачи сообще­ния на соединениии надводных кораблей (рис. 4.5.4). Заметим, что в данном полносвязном графе отсутствуют пели. По этой причине элементы главной диагонали имеют матрицы Т значение .

В графе вершины соответствуют кораблям, а дуги – каналам обмена информацией между двумя кораблями (возможные отрезки маршрута передачи сообщения). Стоимость каждой дуги t_ij соответствует времени передачи сообщения с i–го корабля на j–й корабль.

Рис. 4. Гамильтоновы контура

Маршруту передачи сообщения на все корабли соединения соответствует гамильтонов контур, содержащий все вершины графа (кроме первой) по одному разу, начинающийся и заканчивающийся в первой вершине.

Для получения оценки нижней границы длин всех гамильтоновых контуров (времени передачи сообщения на все корабли) воспользуемся той особенностью, что в каждый гамильтонов контур входит только по одному элементу из каждой строки и из каждого столбца. Поэтому если элементы любой строки или любого столбца матрицы Т уменьшить на какое-либо число, то на это же число уменьшаются длины всех гамильтоновых контуров.

На этом свойстве основан метод приведения матрицы Т по строкам и столбцам:

• из элементов каждой строки матрицы Т вычитается минимальное значение. В результате получается приведенная по строкам матрица Т. Одновременно длины всех гамильтоновых контуров уменьшаются на сумму минимальных значений в каждой строке матрицы Т;

• из элементов каждого столбца приведенной по строкам матрицы Т вычитается минимальное значение. В результате получается приведенная по столбцам матрица Т. Одновременно длины всех гамильтоновых контуров (возможных маршрутов передачи сообщения на корабли соединения) уменьшаются на сумму минимальных значений в каждом столбце матрицы Т ;

• исходная нижняя граница длины маршрута передачи сообщения на корабли соединения равна .

Ш

1 2 3 4 5

1 2 3 4 5

аг 1. Определение нижней границы времени передачи сообщения. В примере 3 после приведения по строкам и столбцам W_н = 10 + 1=11. Матрицы Т и Т выглядят следующим образом:



1 2 3 4 5

В результате приведения матрицы Т по столбцам изменяется только четвертый столбец. Теперь каждая строка и каждый столбец имеют хотя бы по одному нулю.

Способ разбиения множества допустимых решений на два подмножества в данном примере заключается в следующем: выберем одну из дуг (i, j) и разобьем исходное множество всех гамильтоновых контуров на на два подмножества. К первому подмножеству отнесем все гамильтоновы контуры, которые содержат эту дугу (i, j), а ко второму – все гамильтоновы контуры, которые не содержат эту дугу (i, j).

Матрица Т, соответствующая первому подмножеству, преобразуется в матрицу Т₁ путем исключения i–й строки и j–го столбца с последующим приведением по строкам и столбцам.

Элементу t_ji в матрице Т₁ следует присвоить значение  для того чтобы исключить возможность получения не гамильтоновых контуров (т. е. чтобы исключить возможность попаданию в i–ю вершину второй раз, на сей раз из вершины j).

Какую же дугу выбрать? Выбирать следует такую дугу, что:

• ее наличие в анализируемом подмножестве минимизирует (оставляет без изменения) оценку нижней границы W_н (т. е. t_ij = 0 в матрице Т);

• ее отсутствие в анализируемом подмножестве прпиводит к максимальному увеличению оценки нижней границы W_н . Новая оценка нижней границы равна W_н +(i, j), где (i, j) – величина на которую увеличится оценка нижней границы при отсутствии дуги (i, j) в анализируемом подмножестве гамильтоновых контуров.

Следовательно для выбираемой дуги должно быть t_ij = 0 в матрице Т и (i, j) – максимально из всех других  для дуг, имеющих нуль в матрице Т.

Способ вычисления (i, j): В матрице Т выбрать любой элемент (i, j), для которого t_ij = 0. Найти минимальный элемент в i–й строке матрицы Т (кроме t_ij ) и сложить его с минимальным элементом j–м столбце матрицы Т (кроме t_ij ). Данная сумма и есть (i, j).

Шаг 2. Выбор дуги, разбивающей исходное множество гамильтоновых контуров на два подмножества.

1 2 3 4 5

Выберем дуги (i, j), для которых в матрице Т t_ij = 0.

Для каждого такого нуля в матрице Т вычислим значения (i, j):

(1, 2)=0, (1, 4)=0, (2, 1)=1, (2, 4)=0, (3, 5)=2, (4, 2)=1, (5, 3)=4.

Таким образом для разбиения исходного множества гамильтоновых контуров следует выбрать дугу (5, 3), т. к. величина, на которую увеличится оценка нижней границы при отсутствии дуги (5, 3)=4 в маршруте передачи сообщения, является максимальной из всех (i, j) для дуг с t_ij = 0 в матрице Т.

Оценка нижней границы времени передачи сообщения по оптимальному маршруту при отсутствии дуги (5, 3) в маршруте изменится и будет равна W_н1 = 11+4=15.

В бинарое дерево поиска (рис. 4.5.5) на втором уровне должны быть включены две вершины: вершина сW_н1 = 15 и вершина (5, 3). Поскольку подмножество гамильтоновых контуров, не содержащих дугу (5, 3), имеет нижнюю границу W_н1 = 15, более всего превышающую нижнюю границу исходного множества гамильтоновых контуров W_н = 11, то подмножество, соответствующее вершине исключается из рассмотрения как не перспективное. Следовательно, необходимо просмотреть подмножество гамильтоновых контуров, обязательно содержащих дугу (5, 3).

Шаг 3. Определение матрицы Т₁, соответствующей подмножеству гамильтоновых контуров, обязательно содержащих дугу (5, 3).

П

1 2 3 4 5

1 2 4 5

реобразуем матрицуТ в матрицу Т₁ путем вычеркивания из матрицы Т 5-й строки и 3-го столбца с заменой значения элемента (3, 5) на : t₃₅ = .

.

Шаг 4. Определение нижней границы времени передачи сообщения по маршруту, обязательно содержащему дугу (5, 3).

Для определения новой нижней границы приведем матрицу Т₁ по строкам и по столбцам:

1 2 4 5

1 2 4 5