165

5.3. Принятие решений в условиях неопределенности и риска

_________________________________________________________________________________________________________

5.3. Принятие решений в условиях неопределенности и риска

В случае принятия решений в условиях определенности его последствия однозначны. Выбор одной из альтернатив хХ оп­ределяется именно этими последствиями. Однако в реальной си­туации с каждой альтернативойхХ связано множество воз­можных исходовY. При этом в момент выбора неизвестно, какой исход реализуется. Это выяснится только после сделанного вы­бора, когда уже ничего изменить нельзя. Неоднозначность ис­ходов связана с ограниченностью и неточностью информации о задаче принятия решений, что приводит к двум типам ситуаций, в которых приходится принимать решения[12]:

1. Принятие решений в условиях риска.

2. Принятие решений при наличии неопределенности.

В первом случае степень неполноты данных выражается через функцию распределения вероятностей. Во втором случае существование подобных функций не гарантируется. Таким образом, принятие решений в условиях определенности и в условиях неопределенности представляют собой два крайних случая. Принятие решений в условиях риска определяет промежуточную ситуацию.

Принятие решения в условиях неопределенности

Стратегии принятия решений в условиях неопределенности

Рассмотрим выбор в условиях неопределенности. Простейшей задачей выбора в этом случае является выбор в условиях конфликта. В этом случае сталкиваются интересы двух (или более) сторон, преследующих разные (иногда противоположные) цели. Теория игр представляет собой математическую теорию конфликтных ситуаций. В них взаимодействующие стороны называются игроками, выбираемые альтернативы называются ходами; правила выбора хода называются стратегиями. Ходы бывают личные и случайные. При личном ходе игрок сознательно выбирает и осуществляет тот или иной вариант действий. При случайном ходе выбор варианта действий осущест­вляется каким-либо механизмом случайного выбора. В зависи­мости от числа стратегий (конечного и бесконечного) игры де­лятся на конечные и бесконечные игры.

Оптимальной стратегией игрока называется такая, которая обеспечивает ему наилучшее положение в данной игре, т.е. максимальный выигрыш.

Парная игра при конечном множестве альтернатив игро­ков Х и Yможет быть описана матрицей

G=,

где ,n– число ходов первого игрока,m– число ходов первого игрока.

Числа g_ijозначают выигрыши первого игрока, когда первым игроком сде­лан ходx_i, а вторым игроком – ходу_j.

При этом матрица G, оценивающая ситуацию с точки зрения одного игрока, уже недостаточна для описания игры. Необходимо задать вторую матрицуU=, описывающую интересы второ­го игрока. Расхождения между этими матрицами определяет сте­пень антагонизма игроков. Еслиg_ij +u_ij=const, то такая игра определяет строгое соперничество. В случае, еслиg_ij+u_ij= 0, то имеем игру с нулевой суммой. Тогда для задания игры дос­таточно определить только одну матрицу, например матрицуG. Выигрыш одного игрока будет проигрышем другого и наоборот.

Для решения таких задач выбора используется критериальный язык выбора. Однако в силу неопределенности исхода нужно дать оценку сразу всей строке матрицы, соответствующей x_i. По та­ким оценкам можно сделать выбор.

Критерии выбора хода при принятии решений в условиях неопределенности

Самым распространенным для такого выбора является максиминный (минимаксный) критерий. Здесь в каждой строке матрицы находится наименьший выигрыш первого игрока(в каждом столбце наибольший проигрыш второго игрока), который гарантирует выигрыш или проигрыш в самом худшем варианте исхода игры и считается оценкой альтернативыx_i.

Затем производится выбор альтернативы по iиjв соответствии с правилами(или). Отличие максиминного и минимаксного критерия состоит в том, что анализируются выигрыши или проигрыши игроков. При этом.

В тех случаях, когда =, точка (i,j) одновременно удовлетворяет обоих игроков. Эта точка равновесия называется седловой точкой. Отход от нее не выгоден для обеих сторон.Поэтому седловая точка является решением (ценой) игры.

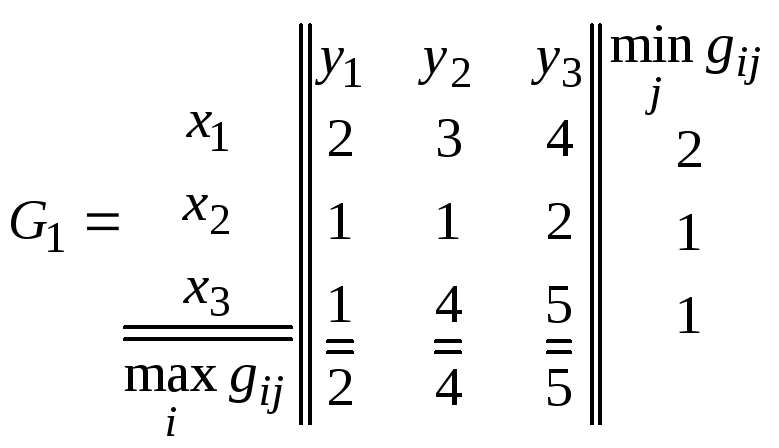
Рассмотрим, например, матрицу G₁ для такой игры (пример 1):

Седловой точной является точка (x₁,y₁), оптимальным ходом игрока Х является ходx₁, обеспечивающий выигрышg₁₁=2, а оптимальным ходом игрока Y - ходy₁, обеспечивающий про­игрышg₁₁=2.

Наличие седловой точки в игре - это далеко не правило, а скорее исключение. Если игра не имеет седловой точки, то возникают затруднения в определении цены игры и оптимальных стратегий игроков.

Рассмотрим, например, матрицу G₂, не имеющую седловой точки (пример 2).

В этой игре максимин равен 3, а минимакс - 4. Следова­тельно, первый игрок может гарантировать себе выигрыш - 3, а второй игрок проигрыш - 4. Это невыгодно второму игроку, т.к. он будет проигрывать больше, чем гарантирует себе выиграть первый игрок. Однако если второй игрок будет знать, что первый выберет ход x₃, то он выберет ходy₂, чтобы уменьшить свой проигрыш до 3.

В свою очередь, если первый игрок узнает о выборе вторым игроком хода у₂, он выбирает ходх₂для выигрыша равного 5 т.д. Таким образом, возникает ситуация, когда игроки должны хранить в секрете свои стратегии. При многократной игре сек­ретность можно сохранить, если стратегию каждый раз выбирать случайным образом. Тогда противник не сможет заранее узнать о действии другой стороны.

Если допустить, что каждый из трех ходов игры G₂для обоих игроков равновероятен, то средний выигрыш первого иг­рока

g_ср=,

где =,=- рас­пределение вероятностей выбора ходов первым и вторым игроками.

Таким образом, выигрыш больше гарантированного выигрыша первого игрока при чистой стратегии и меньше гарантированного проиг­рыша второго игрока.

Стратегии, основанные на случайном выборе, называются смешанными, в отличие от ранее рассмотренных чистых страте­гий, в которых альтернатива выбирается однозначно по детер­минированному правилу. Смешанные стратегии представляют со­бой модель изменчивой, гибкой тактики, когда ни один из иг­роков не знает, как поведет себя противник.

Существует основная теорема теории игр:

 Любая конечная игра двух лиц с нулевой суммой имеет, по крайней мере, одно решение - пару оптимальных стратегий, в общем случае смешан­ных, и соответствующую цену g. Если один из игроков придержи­вается своей оптимальной стратегии, то другому не выгодно отступать от своей стратегии. Эта пара образует положение рав­новесия: один игрок хочет обратить выигрыш в максимум, получая g (если g > 0), другой игрок хочет обратить проигрыш в минимум, получая – g.

В рассмотренной игре предполагается, что игроки делают самые правильные выводы, принимают единственно правильное решение. Считается, что каждому игроку известны все возможные стратегии противника, неизвестно лишь какой именно стратегией он пользуется в данной партии игры. Поэтому применяемые максиминные или минимаксные критерии являются самыми осторожными, пессимистическими. Они рассчитаны на самый неблагоприятный исход игры вследствие сделанного выбора.

Если ослабить пессимизм оценки, то возможны другие критерии. Таков, например, критерий минимаксного сожаления Сэвиджа. В этом случае по платежной матрице G вычисляется матрица сожалений (матрица риска) R.

Каждый элемент матрицы риска для первого игрока вычисляется как разность максимального числа в строке и каждого элемента строки .

Каждый элемент матрицы риска для второго игрока вычисляется как разность каждого элемента столбца и минимального числа в столбце .

Затем к этой матрице, как для первого, так и для второго игрока применяется минимаксный критерий

Дальнейшее ослабление пессимизма дает критерий пессимизма-оптимизма Гурвица, который представляет собой взвешенную комбинацию наилучшего и наихудшего исходов. При этом значение коэффициентааопределяет степень пессимизма

Если а= 1, то, т.е. этот критерий превращается вмаксимин.

Наибольший оптимизм будет получен при равенстве коэффициента анулю (а = 0):.

В критерии Лапласасчитается, что все возможные ходы противника равновероятны:

,.

Для матрицы G₂ ;.

Данные критерии также применяются в таких задачах, для которых неопределенность появляется не вследствие противо­действия противника, а вследствие ограниченности и неточности информации о внешней среде или природе. Природа может находиться в одном из состояний . В отличие от игр, в которых каждый из игроков стремится так выбрать стратегию, чтобы получить для себя наибольшую выгоду, в "играх против природы", называемых также статистическими играми, один из игроков ("природа") оказывается нейтральным. Природа не имеет злого умысла по отношению к человеку. Она просто развивается по своим законам, которые человек не знает или знает недостаточно полно. Правда, у человека есть еще возможность изучать природу посредством проведения экспериментов.