Определение степени согласованности мнений экспертов

Групповая оценка, получаемая при групповых методах оп­роса, может остаться достаточно надежной только при условии хорошей согласованности ответов экспертов [12].

В общем случае после проведения оценивания необходимо провести статистический анализ получаемых результатов.

Определение степени согласованности мнений экспертов с использованием распределения Стьюдента

Степень согласованности мнений экспертов при численных оценках (полученных, например, методом непосредственной оценки) определяется с помощью дисперсии  ² или оценки дисперсии ;

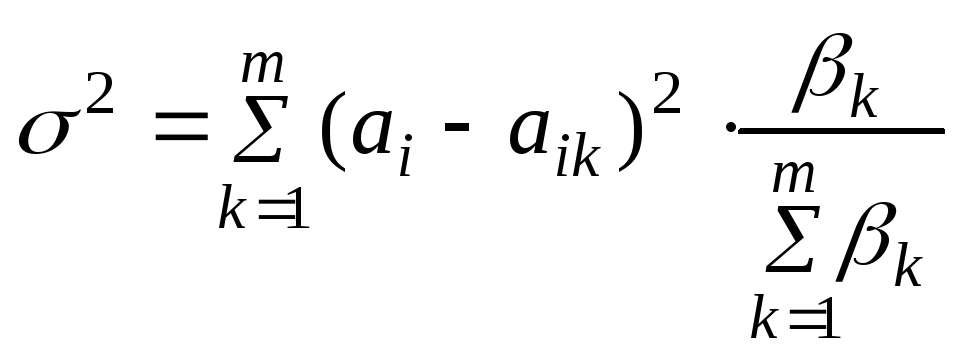или ,

где a_i – математическое ожидание оценки альтернативы по i-му критерию m экспертами,

–среднее арифметическое оценок альтернативы по i-му критерию m экспертами.

Если веса экспертов не установлены:

.

Задавшись уровнем значимости _i, можно определить границы интервала, в котором будет находиться результирующая оценка а:

, где .

Величина t имеет распределение Стьюдента с m – 1 степенями свободы.

Пусть, например, десять экспертов с одинаковыми _k = 1 оценивают среднее время наработки на отказ радиотехнической аппаратуры корабельной АСУ. В результате оценки получены следующие значения T_i в часах: Т₁ = 40; Т₂ = 42; Т₃ = 38; Т₄ = 44; Т₅ = 37; Т₆ = 34; Т₇ = 46; Т₈ = 45; Т₉ = 33; Т₁₀ = 42.

Результирующая оценка, рассчитанная как среднее арифметическое данных 10 оценок:

= 40,1 ч;  ² = 18,29 ч ²;  = 4,28 ч.

Задав уровень значимости  = 0,05, по таблицам распределения Стьюдента определим значение t для числа степеней свободы m – 1 = 9. Тогда t = 2,26.

= 3,06 ч.

Таким образом: 37,04 < Т < 43,16 ч.

В данном примере относительный (нормализованный) коэффициент согласованности мнений экспертов меньше 0,1: 0,076 < 0,1.

Если относительный (нормализованный) коэффициент согласованности мнений экспертов больше 0,1, т. е. интервал, в котором находится оцениваемая вели­чина, является большим, то данный факт говорит о том, что мнения экспертов недостаточно согласо­ваны. Для повышения согласованности оценок необходим допол­нительный сеанс экспертизы.

Оценка согласия экспертов

при использовании методов ранжирования с помощью коэффициента конкордации (согласия) W.

Для процедуры строгого ранжирования .

Для процедуры нестрогого ранжирования

,

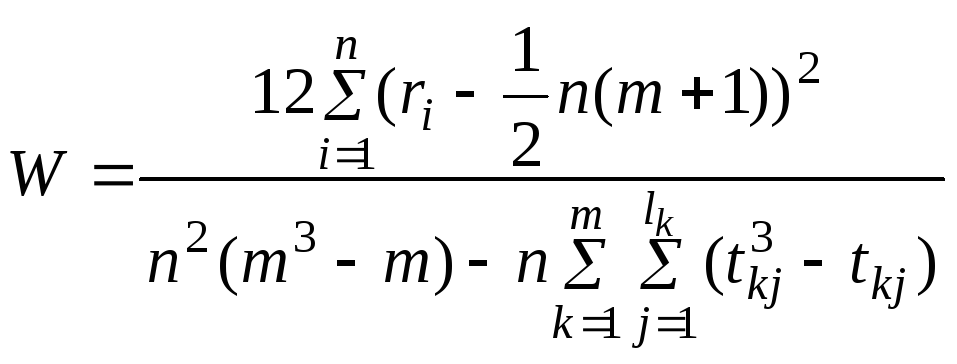где – число групп равных рангов, введенных k–м экспертом;

t_kj – количество дробных рангов в j–й () группе, введенныхk–м экспертом;

r_i – сумма рангов, присвоенных i–й альтернативе;

m – количество экспертов;

n – количество сравниваемых альтернатив.

Статистическую значимость ранжировки проверяют следующим образом. Выбирают значение . Вычисляют величину . Из таблиц распределения² для числа степеней (m–1) находят табличное значение величины . В том случае, если полученное значениебольше табличного, полученная ранжировка статистически значима. В противном случае необходимо организовать дополнительный сеанс экспертизы.

Оценим статистическую значимость ранжировки из таблицы 1. Эта ранжировка является нестрогой. Она содержит группы равных рангов у всех экспертов кроме восьмого, десятого и двенадцатого:

m = 12, n =7;

r₁=63,5, r₂=78,5, r₃=23, r₄=69, r₅=19, r₆=35,5, r₇=47,5,

=1, =1, =2, =1, =1, =1, =1, =0, =1, =0, =1, =0;

t₁₁=2, t₂₁=2, t₃₁=2, t₃₂=2, t₄₁=2, t₅₁=2, t₆₁=2, t₇₁=2, t₉₁=2, t_11.1=2.

W = 0,47; = 7110,47 = 36,19.

Для значения  = 0,05 и числа степеней свободы из таблиц распределения² получаем ²_0,05(11) = 19,675, что соответствует табличному значению величины . Так как= 36,19 >= 19,675, то полученная ранжировка является статистически значимой.

Пример 1.

Путем проведения экспертного опроса среди обучаемых и обработки его результатов методом непосредственной оценки упорядочить дисциплины, изучаемые во втором семестре 3-го курса, по убыванию заинтересованности обучаемых. Каждому эксперту парное сравнение дисциплин производить по 9-ти бальной шкале, используя степенную калибровку. Сопос­тавление каждой дисциплине ее численной оценки каждым экспертом произвести, используя модель равномерного сглаживания. Определить относительный коэффициент согласованности мнений экспертов с использованием распределения Стьюдента.

Пусть тремя экспертами будут оцениваться четыре дисциплины: «Теория принятия решений» (ТПР – индекс 1), «Системы реального времени» (СРВ – индекс 2), «Информационные технологии» (ИТ – индекс 3), «Сетевые технологии» (СТ – индекс 4).

Пусть первый эксперт произвел сравнение дисциплин попарно по 9-ти бальной шкале следующим образом:

ТПР существенно интересней, чем СРВ (5),

ТПР намного интересней, чем ИТ (7),

ТПР намного интересней, чем СТ (7);

СРВ немного интересней, чем ИТ (3),

СРВ существенно интересней, чем СТ (5);

ИТ чуть-чуть интересней, чем СТ (2).

Тогда, используя степенную калибровку, можно составить следующую степенную матрицу суждений первого эксперта:

.

Используя модель равномерного сглаживания, вычислим геометрические средние оценок каждой дисциплины первым экспертом: . Тогда оценка интересности каждой дисциплины первым экспертом будет равна.

;

;

; .

;

;

;

.

Пусть оценки интересности дисциплин вторым экспертом, также вычисленные с использованием модели равномерного сглаживания, будут равны:

А оценки интересности дисциплин третьим экспертом, также вычисленные с использованием модели равномерного сглаживания, пусть будут равны:

Обрабатывая оценки экспертов методом непосредственной оценки в соответствии с формулой , получаем оценки для каждой дисциплины:

;

;

;

.

Упорядочивая дисциплины по убыванию значений , получаем их ранжирование: ТПР, СРВ, ИТ, СТ.

Теперь оценим согласованность мнений экспертов, определяя относительный коэффициент согласованности мнений экспертов с использованием распределения Стьюдента.

Так как веса экспертов будем считать равными 1, то для определения оценок дисперсий оценок интересности дисциплин, полученных после обработки мнений экспертов можно использовать формулу . Тогда

Задав уровень значимости  = 0,05, по таблицам распределения Стьюдента определим значение t для числа степеней свободы m – 1 = 3. Тогда t = 4,3.

; ;

; .

Вычислим относительный (нормализованный) коэффициент согласованности мнений экспертов:

>0,1; >0,1;

>0,1; >0,1.

Тот факт, что относительные коэффициенты согласованности мнений экспертов намного больше 0,1, говорит о том, что мнение экспертов не согласовано, а количество экспертов в группе слишком мало.

Однако, если определять согласованность мнений экспертов путем проверки статистической значимости ранжировки при помощи коэффициента конкордации, то мнения экспертов по упорядочиванию дисциплин окажутся согласованными.

Эксперты	ТПР	СРВ	ИТ	СТ
1	1	2	3	4
2	1	2	3	4
3	2	1	3	4
Сумма рангов	4	5	9	12

Данное ранжирование оказалось строгим. Поэтому коэффициент конкордации может быть вычислен по формуле , где n=4 – количество альтернатив (дисциплин), m=3 – количество экспертов.

.

.

Из таблиц распределения ² для числа степеней (m–1)=2 найдем табличное значение величины =5,991 для значения = 0,05.

Поскольку >=5,991, то мнения экспертов по ранжированию дисциплин можно считать согласованными, а полученную ранжировку – статистически значимой.

Если сразу провести ранжирование альтернатив для экспертов оказывается затруднительным, то каждый эксперт может производить парное сравнение альтернатив с выставлением оценок:

«1» для лучшей альтернативы из двух альтернатив,

«0» для лучшей альтернативы из двух альтернатив,

«½» для каждой из двух эквивалентных, с точки зрения эксперта, альтернатив.

Таким образом, каждый эксперт заполняет матрицу парных сравнений. Сумма элементов в строке соответствует значимости альтернативы. Поэтому каждый эксперт может упорядочить альтернативы в порядке убывания сумм элементов в строках матрицы парных сравнений. Если для нескольких строк суммы элементов, то альтернативы, которым соответствуют эти строки, при ранжировании получают равные стандартизированные ранги.

Затем согласованность мнений экспертов по проведению ранжирования альтернатив можно определить путем проверки статистической значимости ранжировки при помощи коэффициента конкордации.

Упражнения:

1. Путем проведения экспертного опроса и обработки его результатов методом непосредственной оценки упорядочить дисциплины, изучаемые во втором семестре 3-го курса, по убыванию сложности. Каждому эксперту парное сравнение дисциплин производить по 9-ти бальной шкале, используя степенную калибровку. Сопос­тавление каждой дисциплине ее численной оценки каждым экспертом произвести, используя модель равномерного сглаживания. Определить относительный коэффициент согласованности мнений экспертов с использованием распределения Стьюдента.

2. Путем проведения экспертного опроса и обработки его результатов методом ранжирования упорядочить дисциплины, изучаемые во втором семестре 3-го курса, по убыванию сложности. Каждому эксперту произвести нестрогое ранжирование с выставлением стандартизированных рангов для эквивалентных, с точки зрения эксперта, альтернатив. Определить согласованность мнений экспертов и проверить статистическую значимость ранжировки при помощи коэффициента конкордации.

3. Методом последовательных предпочтений на основании собственного мнения определить нормированные веса дисциплин, изучаемых во втором семестре 3-го курса, упорядоченных в соответствии с заданием 1 или 2. Порядок дисциплин не менять.

Контрольные вопросы:

1. В чем заключается смысл задачи оценивания?

2. Как должен действовать исследователь при проведении экспертизы?

3. Каким должен быть размер группы экспертов?

4. Назовите методы проведения экспертного опроса.

5. Перечислите методы обработки экспертной информации.

6. Дайте характеристику метода непосредственной оценки.

7. Когда при проведении экспертизы используются методы ранжирования?

8. Поясните различия между строгим и не строгим ранжированием.

9. Что такое стандартизированный ранг альтернативы?

10. Дайте характеристику метода последовательных предпочтений.

11. Дайте характеристику метода парных сравнений.

12. Какими способами может определяться согласованность мнений экспертов при численных оценках альтернатив и при проведении их ранжирования?

13. Как производится оценка степени согласованности мнений экспертов с использованием распределения Стьюдента?

14. Как производится оценка степени согласованности мнений экспертов с использованием коэффициента конкордации и распределения ²?