Особые виды отношений.

 Отношение называется пустым , если оно не выполняется ни для одной пары x, y. Для пустого отношения:

• матрица А() такая, что а_ij = 0 для всех i, j;

• граф G() не имеет дуг;

• верхнее и нижнее сечение для любого элемента множества  есть : ⁺(x)=^–(x)= для  x.

 Отношение называется полным , если оно выполняется для всех пар x, y. Для полного отношения:

• матрица А() такая, что а_ij = 1 для всех i, j;

• граф G() такой, что дуги соединяют любую пару вершин (направлены в обе стороны), в том числе при каждой вершине имеются петли;

• верхнее и нижнее сечение для любого элемента множества  есть : ⁺(x)= ^–(x)= для  x.

 Отношение называется диагональным E (отношением равенства), если оно выполняется для всех пар x, y, состоящих из совпадающих элементов. Т. е. xEy только в том случае, если x и y – один и тот же элемент из множества . Для диагонального отношения:

• матрица А(E) такая, что а_ij = 1 для всех i=j и а_ij = 0 для всех ij;

• граф G(E) такой, что при каждой вершине имеются только петли, а все другие дуги отсутствуют;

• верхнее и нижнее сечение для любого элемента x множества  есть {x}: E ⁺(x)=E ^–(x)={x} для  x.

 Отношение называется антидиагональным , если оно выполняется для всех пар x, y, состоящих из несовпадающих элементов. Т. е. xy только в том случае, если x и y – различные элементы из множества . Для антидиагонального отношения:

• матрица А() такая, что а_ij = 0 для всех i=j и а_ij = 1 для всех ij;

• граф G() такой, что при каждой вершине отсутствуют петли, а все другие дуги обязательно присутствуют;

• верхнее и нижнее сечение для любого элемента x множества  есть полное множество , за исключением фиксированного элемента x:

⁺(x)=^–(x)= \{x} для  x.

Операции над бинарными отношениями.

 Вложение отношений: Отношение R₁ вложено в отношение R₂ (R₁≤R₂), если множество пар, для которых выполняется R₁, содержится во множестве пар, для которых выполняется R₂. Например, отношение «меньше» вложено в отношение «меньше или равно».

 Вложение строгого порядка: Отношение R₁ строго вложено в отношение R₂ (R₁R₂), если R₁≤R₂ и R₁R₂.

 Дополнение отношений: Отношение называется дополнением отношения R, если оно выполняется только для тех пар из множества всех пар , для которых не выполняется отношение R:=²\ R.

Для дополнения отношения R:

• матрица А() такая, что а_ij() = 1 - а_ij(R) для всех i, j;

• граф G() такой, что в нем имеются только те дуги, которые отсутствуют в графе G(R);

• верхнее сечение для любого элемента x множества :

⁺(x)= \ R⁺(x);

• нижнее сечение для любого элемента x множества :

^–(x)= \ R^–(x).

 Пересечение отношений: Отношение R₁R₂ называется пересечением отношений R₁ и R₂, если множество пар R₁R₂ альтернатив из множества всех пар альтернатив  является пересечением соответствующих подмножеств R₁ и R₂ из множества всех пар альтернатив .

Для пересечения R₁R₂ отношений R₁ и R₂:

• матрица А(R₁R₂) такая, что а_ij(R₁R₂) = 1, если а_ij(R₁) = 1 и а_ij(R₂) = 1 для всех i, j;

• граф G(R₁R₂) такой, что в нем имеются те дуги, которые имеются и в графе G(R₁), и в графе G(R₂);

• верхнее сечение для любого элемента x множества : R₁R₂⁺(x)= R₁⁺(x)R₂⁺(x);

• нижнее сечение для любого элемента x множества : R₁R₂^–(x)= R₁^–(x)R₂^–(x).

Если отношение R₁ – «не меньше», а отношение R₂ – «не больше», то R₁R₂ есть отношение «равно».

 Объединение отношений: Отношение R₁R₂ называется объединением отношений R₁ и R₂, если множество пар R₁R₂ альтернатив из множества всех пар альтернатив  является объединением соответствующих подмножеств R₁ и R₂ из множества всех пар альтернатив .

Для объединения R₁R₂ отношений R₁ и R₂:

• матрица А(R₁R₂) такая, что а_ij(R₁R₂) = 1, если либо а_ij(R₁) = 1, либо а_ij(R₂) = 1 для всех i, j;

• граф G(R₁R₂) такой, что в нем имеются те дуги, которые имеются либо в графе G(R₁), либо в графе G(R₂);

• верхнее сечение для любого элемента x множества : R₁R₂⁺(x)= R₁⁺(x)R₂⁺(x);

• нижнее сечение для любого элемента x множества : R₁R₂^–(x)= R₁^–(x)R₂^–(x).

Если отношение R₁ – «больше», а отношение R₂ – «равно», то R₁R₂ есть отношение «больше или равно» («не меньше»).

 Обращение отношений: Обратным отношением R^-1 к отношению R называется отношение, определяемое условием x R^-1y  y R x, т. е. если отношение R: «больше», то отношение R^-1: «меньше»; если отношение R: «быть начальником», то отношение R^-1: «быть подчиненным». (Но отношение «не быть начальником» является дополнением к отношению R: «быть начальником»).

Для обратного отношения R^-1 по сравнению с отношением R:

• матрица А(R^-1) такая, что а_ij(R^-1) = а_ji (R) для всех i, j;

• граф G(R^-1) такой, что в нем имеются только те же дуги, которые имеются в графе G(R), но направлены они в противоположные стороны;

• верхнее сечение для любого элемента x множества : R^-1+(x)= R^–(x);

• нижнее сечение для любого элемента x множества : R^-1–(x)= R⁺(x).

 Двойственность отношений: Двойственным отношением R^d к отношению R называется отношение дополнительное к обратному отношению R^-1 или обратное к дополнительному отношению : R^d == ()^-1, т. е. если отношение R: «больше», то отношение R^d: «не меньше»; если отношение R: «быть начальником», то отношение R^d: «не быть подчиненным». Для двойственного отношения R^d по сравнению с отношением R:

• матрица А(R^d) такая, что а_ij(R^d) = а_ij(R) для всех i, j, таких что i j, и а_ij(R^d) = для всех i, j, таких что i= j;

• граф G(R^d) такой, что в нем имеются только те же дуги между различными вершинами, которые имеются в графе G(R), но петли при вершинах присутствуют в графе G(R^d) только в том случае, если они отсутствуют в графе G(R);

• верхнее сечение для любого элемента x множества :

или R^{d +}(x)= R⁺(x)\{x}, если x R x, или R^{d +}(x)= R⁺(x) {x}, если xx;

• нижнее сечение для любого элемента x множества :

или R^{d –}(x)= R^–(x)\{x}, если x R x, или R^{d –}(x)= R ^–(x) {x}, если xx.

 Произведение отношений: Произведением отношений R₁ и R₂ на множестве  (R₁; R₂; x, y) называется отношение R₁ R₂, такое, что x R₁ R₂ y имеет смысл только тогда, когда  z, для которого x R₁ z и z R₂ y.

Например, если отношение R₁: «быть братом», а отношение R₂: «быть родителем», то отношение R₁ R₂ будет отношением «быть дядей», если найдется такой человек z, для которого человек x приходится братом, и который является родителем для человека y. Тогда x R₁ R₂ y означает, что человек x приходится дядей человеку y.

Для произведения R₁ R₂ отношений R₁ и R₂:

• матрица А(R₁R₂) такая, что а_ij(R₁ R₂) = 1, если а_ik(R₁)=1 и а_kj (R₂)=1 для всех i, j;

• граф G(R₁R₂) такой, что в нем имеются дуги между двумя вершинами x и y, только тогда, когда из первой вершины x выходит дуга в вершину z в графе G(R₁), а из вершины z выходит дуга во вторую вершину y в графе G(R₂);

• верхнее сечение для любого элемента x множества :

R₁R₂⁺(x) = {y   | (y, z  R₁,  z, x  R₂)};

• нижнее сечение для любого элемента x множества :

R₁R₂^–(x) = {y   | (x, z  R₁,  z, y  R₂)}.

 Сужение отношений: Отношение R₁, ₁ называется сужением отношения R,  на подмножество ₁ множества , если ₁ и R₁= R₁₁. Граф такого отношения G(R₁) является подграфом G(R). Например, отношение R₁ «быть более способным к обучению» на множестве ₁ (курсантов 333 класса) является сужением отношения R «быть более способным к обучению» на множестве  (курсантов 33 роты), так как все пары курсантов множества R₁ войдут во множество пар курсантов R.

 Изоморфные отношения: Отношение называется изоморфным, если  отображение  ₁  ₂ (x, y₁;  (x),  (y)₂) такое, что x R₁ y   (x) R₂  (y),

где R₁ – отношение, заданное на множестве ₁,

R₂ – отношение, заданное на множестве ₂.

Имеется прямое и обратное соответствие оригинала и образа и наоборот.

Например, личное дело лучшего курсанта лучше личного дела худшего по сравнению с ним курсанта. И наоборот, курсант, личное дело которого лучше, является лучше, чем курсант, личное дело которого лучше. Если же личные дела курсантов не достаточно объективно отражают самих курсантов, то налицо гомоморфизм.

 Гомоморфные отношения: Отношение называется гомоморфным, если  отображение  ₁  ₂ (x, y₁;  (x),  (y)₂) такое, что x R₁ y   (x) R₂  (y),

где R₁ – отношение, заданное на множестве ₁,

R₂ – отношение, заданное на множестве ₂.

Имеется прямое соответствие оригинала и образа, но обратное соответствие и обратное не обязательно.

Например, в классном журнале отличные оценки получают лучшие курсанты, но отсутствие отличных оценок у курсанта еще не говорит о том, что он не способный ученик: возможно он болел или стоял на дежурстве и поэтому не получил свою отличную оценку.

Свойства отношений.

Рассмотрим некоторые важнейшие свойства отношений, которые позволяют выделять классы отношений, применяющиеся в теории выбора и принятия решений.

 Отношение R называется рефлексивным, если диагональное отношение E вложено в отношение R: E  R. Иначе говоря, для всех x в рефлексивном отношении выполняется x R x.

Для рефлексивного отношения:

• в матрице А(R) на главной диагонали стоят единицы;

• в графе G(R) при каждой вершине есть петля;

• верхнее сечение для любого элемента x множества  содержит этот элемент x: x R⁺(x);

• нижнее сечение для любого элемента x множества  содержит этот элемент x: x R^–(x).

Пример рефлексивного отношения: «быть не старше», «больше или равно».

 Отношение R называется антирефлексивным, если оно не пересекается с диагональным отношением: RE=. Иначе говоря, антирефлексивное отношение выполняется лишь для несовпадающих элементов, т. е. x R y, если x  y. Антирефлексивное отношение вложено в антидиагональное отношение: R.

Для антирефлексивного отношения:

• в матрице А(R) на главной диагонали стоят нули;

• в графе G(R) при любой вершине отсутствует петля;

• верхнее сечение для любого элемента x множества  не содержит этот элемент x: xR⁺(x);

• нижнее сечение для любого элемента x множества  не содержит этот элемент x: xR^–(x).

Пример антирефлексивного отношения: «быть больше», «быть победителем».

 Отношение R называется симметричным, если R  R^-1, т. е. если выполняется x R y, то обязательно выполняется и y R x.

Для симметричного отношения:

• матрица А(R) симметрична относительно главной диагонали: а_ij= а_ji для всех i, j;

• в графе G(R) если есть дуга (x, y), то обязательно есть дуга (y, x);

• верхнее и нижнее сечение совпадают для любого элемента x множества : R⁺(x)= R^–(x).

Пример симметричного отношения: «быть курсантом одного курса», «быть похожим».

 Отношение R называется асимметричным, если R  R^-1= , т. е. если при любых x и y из множества  выполняется x R y, то не выполняется и y R x и наоборот.

Для асимметричного отношения:

• матрица А(R) несимметрична относительно главной диагонали: а_ij(R)а_ji(R)=0 для всех i, j, т. е. на главной диагонали находятся нули;

• граф G(R) не может одновременно содержать дугу (x, y) и дугу (y, x), петель при вершинах нет;

• если нижнее сечение любого элемента x множества  содержит элемент y, то нижнее сечение элемента y множества  не содержит элемент x: x R^-(y), если y R^–(x). Причем xR^-( x).

Пример асимметричного отношения: «быть больше», «быть начальником».

 Отношение R называется антисимметричным, если R  R^-1 E, т. е. x R y и y R x выполняются одновременно только, если x = y.

Для антисимметричного отношения:

• матрица А(R) несимметрична относительно главной диагонали: а_ij(R)а_ji(R)=0 для всех i, j, кроме случая, когда i=j, т. е. на главной диагонали находятся единицы;

• граф G(R) не может одновременно содержать дугу (x, y) и дугу (y, x), если x y; но петли при вершинах есть;

• если нижнее сечение любого элемента x y множества  содержит элемент y, то нижнее сечение элемента y множества  не содержит элемент x: xR^-(y), если yR^–(x), но xR^–(x).

Примеры антисимметричного отношения: «быть больше или равно», «не быть подчиненным».

 Отношение R называется транзитивным, если R²  R.

Иначе говоря, если x R z и z R y, то x R y. Если же x R z₁, z₁ R z₂, …, z_k-1 R y, то x R y.

Для транзитивного отношения:

• матрица А(R), такая что: а_ik(R)а_kj(R)  а_ij(R) для всех i, j, k, (n – мощность множества ), т. е. логическая сумма произведений элементов i–й строки с соответствующими элементами j–го столбца должна быть не больше а_ij(R). Это означает, что если найдется хотя бы один элемент x_k, такой что x_i находится в отношении R с x_k, а x_k находится в отношении R с x_j, то x_i находится в отношении R с x_j.

• граф G(R) обязательно содержит дугу (x, y), если существует путь из вершины x в вершину y хотя бы через одну другую вершину z;

• верхнее сечение любого элемента x множества  содержит элемент y, если оно содержит элемент z, верхнее сечение которого содержит элемент y: yR⁺(x), если zR⁺(x) и yR⁺(z).

• нижнее сечение любого элемента x множества  содержит элемент y, если оно содержит элемент z, нижнее сечение которого содержит элемент y: yR^–(x), если zR^–(x) и yR^–(z).

Примеры транзитивного отношения: «меньше или равно», «больше», «быть курсантом одного курса».

 Отношение R называется ацикличным, если R^k  R^-1= для  k.

Т. е. если x R z₁, z₁ R z₂, …, z_k-1 R y, то x  y (т. е. y не находится в отношении R с x).

Для ацикличного отношения:

• матрица А(R), такая что: если а_ik(R)а_kj(R) = 1,то а_ji(R) = 0 для всех i, j, k, (n – мощность множества ), т. е. если логическая сумма произведений элементов i–й строки с соответствующими элементами j–го столбца равна 1, то а_ji(R) = 0. Это означает, что если найдется хотя бы один элемент x_k, такой что x_i находится в отношении R с x_k, а x_k находится в отношении R с x_j, то x_j не может находиться в отношении R с x_i.

• граф G(R) не содержит дуги (y, x), если существует путь из вершины x в вершину y хотя бы через одну другую вершину z_i (т. е. в графе отсутствуют циклы);

• верхнее сечение любого элемента x множества  не содержит элемент y, если нижнее сечение элемента x содержит элемент z₀, нижнее сечение которого содержит элемент z₁,…, нижнее сечение которого содержит элемент z_k, нижнее сечение которого содержит элемент y: yR⁺(x), если z₀R^–(x), z₁R^– (z₀), …, z_kR^– (z_k-1) и yR^– (z_k), где k = .

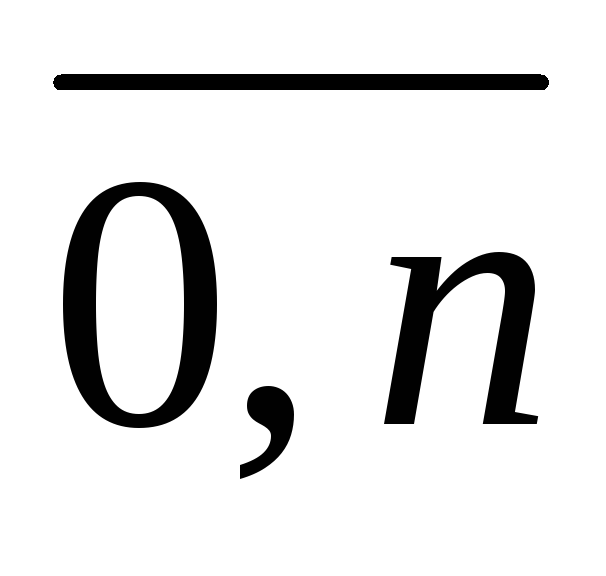• нижнее сечение любого элемента x множества  не содержит элемент y, если верхнее сечение элемента x содержит элемент z₀, верхнее сечение которого содержит элемент z₁,…, верхнее сечение которого содержит элемент z_k, верхнее сечение которого содержит элемент y: yR^–(x), если z₀R⁺(x),z₁R⁺(z₀), …, z_kR⁺( z_k-1) и yR⁺(z_k), где k = .

Примеры ацикличного отношения: «меньше или равно», «больше», «быть начальником», «быть отцом». Причем, отношение «быть отцом» ациклично, но не транзитивно. Так как, если x приходится отцом z, а z приходится отцом y, то x приходится не отцом для y, а дедом, но в то же время y не может приходиться отцом для x, т. к. приходится внуком.

Ацикличность и транзитивность отношений важны для выбора и принятия решения, т. к. они выражают некоторые естественные взаимосвязи между элементами . Действительно, если x в некотором смысле лучше, чем z, а z лучше y, то x также в данном смысле лучше y (свойство транзитивности). В свою очередь y не может быть лучше x (свойство ацикличности).

 Отношение R называется отрицательно транзитивным, если его дополнение транзитивно. Например, отношение «не быть предком» не является транзитивным (т. к. если x не является предком для z, а z не является предком для y, то это еще не означает, что x не является предком для y), а его дополнение «быть предком» является транзитивным.

 Отношение R называется сильно транзитивным, если оно одновременно и транзитивно и отрицательно транзитивно.

Пример такого отношения R: «быть курсантом 333 класса ВМИРЭ». Само отношение транзитивно. Т. к., если x находится в отношении R с z, а z находится в отношении R с y, то это означает, что x находится в отношении R с y, т. е. и x и y являются курсантами 333 класса ВМИРЭ. Дополнение к отношению R есть отношение «не быть курсантом 333 класса ВМИРЭ». Оно также обладает свойством транзитивности. Т. к., если x находится в отношении с z, а z находится в отношении с y, то это означает, что x находится в отношении с y. Т. е. если x и z не являются курсантами 333 класса ВМИРЭ; и z с y не являются курсантами 333 класса, то x и y также не являются курсантами 333 класса.

Если отношение R, заданное на конечном множестве  сильно транзитивно, то существует разбиение множества  на непересекающиеся подмножества _i (= _i), такие что:

1) если x_i, y_j и i  j, то x y;

2) сужение отношения R на любое подмножество _i является либо пустым, либо полным отношением на _i.