1. Вычисление элементов новой ведущей строки.
Новая ведущая строка = Текущая ведущая строка / Ведущий элемент.
2. Вычисление элементов остальных строк, включая z–строку.
Новая строка = Текущая строка – Ее коэффициент в ведущем столбце Новая ведущая строка.
В нашем примере ведущая строка (s1–строка) делится на ведущий элемент (= 6). В следующей таблице показана новая ведущая строка, где вводимая (небазисная) переменная 1 заменила исключаемую переменную s1. В столбце "Решение" получаем новое значение переменной 1 (= 4).
Вычисляем элементы остальных строк таблицы.
1. z–строка.
Текущая z–строка: (1 –5 – 4 0 0 0 0 | 0)
– (–5)Новая ведущая строка: (0 5 10/3 5/6 0 0 0 | 20)
= Новая z–строка: (1 0 –2/3 5/6 0 0 0 | 20)
2. s2–строка.
Текущая s2–строка: (0 1 2 0 1 0 0 | 6)
– (1)Новая ведущая строка: (0 –1 –2/3 –1/6 0 0 0 | –4)
= Новая s2–строка: (0 0 4/3 –1/6 1 0 0 | 2)
3. s3–строка.
Текущая s3–строка: (0 –1 1 0 0 1 0 | 1)
– (1)Новая ведущая строка: (0 1 2/3 1/6 0 0 0 | 4)
= Новая s3–строка: (0 0 5/3 1/6 0 1 0 | 5)
4. s4–строка. Новая s4–строка повторяет текущую s4–строку, поскольку ее коэффициент в ведущем столбце равен нулю.
Новая симплекс-таблица, соответствующая новому базисному решению ( 1, s2, s3, s4), имеет следующий вид.
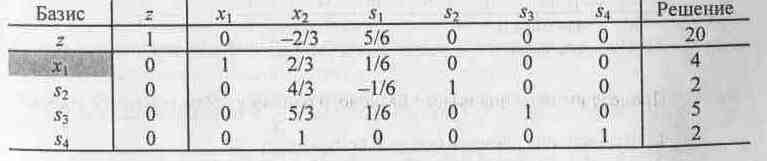
Отметим, что новая таблица обладает теми же свойствами, что и начальная: только небазисные переменные 2 и s1 равны нулю, в столбце "Решение" представлено новое базисное решение ( 1= 4, s2 = 2, s3 = 5, s4 = 2) вместе с новым значением целевой функции z = W() (= 20). Это результат применения метода Гаусса - Жордана.
Из последней таблицы видно, что полученное базисное решение не является оптимальным, поскольку в z–строке переменная 2 имеет отрицательный коэффициент. Так же, как и в начальной таблице, строку z можно интерпретировать как уравнение
Из последнего уравнения следует, что увеличение значения переменной 2 (текущее значение равно нулю) приведет к увеличению значения целевой функции. Таким образом, переменная 2 должна стать вводимой в базис.
Далее определим исключаемую переменную. Для этого вычислим отношения правых частей равенств, соответствующих ограничениям, к коэффициентам, стоящим при 2 в этих равенствах.
Вычисления
показывают, что минимальное (неотрицательное)
отношение соответствует переменной
s2,
которая становится исключаемой; при
этом значение отношения (= 3/2) равно
новому значению переменной
2.
Соответствующее
увеличение значения целевой функции
составит
и
В этой ситуации ведущей строкой будет s2–строка, а ведущим столбцом – столбец, соответствующий переменной 2. Ведущий элемент равен 4/3.
Вычисляем элементы новой симплекс-таблицы:
1. Новая ведущая (s2–) строка = Текущая s2–строка / 4/3
2. Новая строка z–строка = Текущая z–строка–(–2/3)Новая ведущая строка 3. Новая 1–строка = Текущая 1–строка – 2/3 Новая ведущая строка
4. Новая s3–строка = Текущая s3–строка – 5/3 Новая ведущая строка
5. Новая s4–строка = Текущая s4–строка – 1 Новая ведущая строка.
Эти вычисления приводят к следующей таблице.
Поскольку z–строка не имеет отрицательных коэффициентов, соответствующих небазисным переменным s1 и s2, полученное решение оптимально.
Оптимальное решение задачи ЛП можно "считать" из симплекс-таблицы следующим образом.
Неотрицательные (базисные) переменные представлены в столбце "Базис", а их значения – в столбце "Решение". В данном примере имеем следующее.
С помощью симплекс-таблицы можно получить много дополнительной информации (кроме непосредственно оптимального решения).
1. Состояние ресурсов.
2. Цена единицы ресурсов (двойственные цены).
3. Все данные, необходимые для проведения анализа чувствительности оптимального решения.
Покажем, как определить состояние (статус) ресурсов. Нахождение цен единиц ресурсов (так называемых, двойственных цен) и использование данных симплекс-таблицы для проведения анализа чувствительности описано в главе 4 книги Хэмди А. Таха. Введение в исследование операций. М.: Издательский дом «Вильямс», 2001.
Статус ресурса определяется как дефицитный или недефицитный, в зависимости от того, будет он использован полностью или нет. Эту информацию можно получить из результирующей симплекс-таблицы путем проверки значений дополнительных (остаточных) переменных, ассоциируемых с соответствующими ограничениями, накладываемыми на ресурсы. Если дополнительная переменная равно нулю, значит, ресурс использован полностью, и он получает статус дефицитного ресурса. Положительное значение дополнительной переменной указывает на не дефицитность соответствующего ресурса.
В задаче о компании Тиккурила четыре ограничения классифицируются следующим образом.
Статус ресурсов показывает, что, поскольку М1 и М2 дефицитны, их увеличение может привести к улучшению оптимального решения (т.е. увеличению значения целевой функции). Процедура анализа чувствительности может помочь определить, на сколько можно увеличить объемы ресурсов. Этот вопрос исследовался в п. 4.1 учебника. Полное же его рассмотрение представлено в главе 4 книги Хэмди А. Таха. Введение в исследование операций. М.: Издательский дом «Вильямс», 2001.
В предыдущем примере велся поиск максимума целевой функции. В случае минимизации целевой функции, исключаемые переменные определяются точно так же, как и при максимизации целевой функции. Как было показано в лекции 4.1, задача минимизации сводится к задаче максимизации простым соотношением max W() = – тin W(). Поэтому в случае минимизации целевой функции вводимая переменная выбирается как небазисная переменная с наибольшим положительным коэффициентом в z–строке симплекс-таблицы, а минимум целевой функции будет достигнут тогда, когда все коэффициенты в z–строке будут неположительными.
Два правила выбора вводимых и исключающих переменных в симплекс-методе назовем условием оптимальности и условием допустимости. Сформулируем эти правила, а также рассмотрим последовательность действий, выполняемых при реализации симплекс-метода.
Условие оптимальности. Вводимой переменной в задаче максимизации (минимизации) является небазисная переменная, имеющая наибольший отрицательный (положительный) коэффициент в z–строке. Если в z–строке есть несколько таких коэффициентов, то выбор вводимой переменной делается произвольно. Оптимальное решение достигнуто тогда, когда в z–строке все коэффициенты при небазисных переменных будут неотрицательными (неположительными).
Условие допустимости. Как в задаче максимизации, так и в задаче минимизации, в качестве исключаемой выбирается базисная переменная, для которой отношение значения правой части ограничения к положительному коэффициенту ведущего столбца минимально. Если базисных переменных с таким свойством несколько, то выбор исключаемой переменной выполняется произвольно.
Последовательность действий, выполняемых в симплекс-методе.
Шаг 0. Находится начальное допустимое базисное решение.
Шаг 1. На основе условия оптимальности определяется вводимая переменная.
Если вводимых переменных нет, вычисления заканчиваются.
Шаг 2. На основе условия допустимости выбирается исключаемая переменная.
Шаг 3. Методом Гаусса - Жордана вычисляется новое базисное решение. Переход к шагу 1.
Вычисления в симплекс-методе выполняются итерационно в том смысле, что условия оптимальности и допустимости, а также вычисления применяются к текущей симплекс-таблице, в результате чего получается следующая таблица. Мы будем называть последовательные симплекс-таблицы итерациями.
Отслеживание последовательных базисных решений из последнего примера по графическому представлению пространства решений (рис. 1) показывает, что итерационный процесс симплекс-метода начался в крайней (угловой) точке A, затем переместился в крайнюю точку B и закончился в крайней точке C – точке оптимума. Эти итерации соответствуют смежным крайним точкам границы пространства решений. Алгоритм симплекс-метода никогда не сможет переместиться сразу из точки A в точку C.