302

4.2. Симплекс-метод решения задач

линейного программирования

___________________________________________________________________________________________________________

4.2. Симплекс-метод решения задач линейного программирования

Основная идея симплекс-метода

Основываясь на определениях данных в предыдущей лекции, мы можем найти оптимальное решение задачи линейного программирования, записанной в стандартной форме, путем простого перебора всех базисных (допустимых) решений. Но, конечно, такая процедура не эффек­тивна. Алгоритм симплекс-метода находит оптимальное решение, рассматривая ограни­ченное количество допустимых базисных решений [19].

Алгоритм симплекс-метода всегда начинается с некоторого допустимого базисного ре­шения и затем пытается найти другое допустимое базисное решение, "улучшающее" значе­ние целевой функции. Это возможно только в том случае, если возрастание какой-либо нулевой (небазисной) переменной ведет к улучшению значения целевой функции. Но для того, чтобы небазисная переменная стала положительной, надо одну из текущих базисных переменных сделать нулевой, т.е. перевести в небазисные переменные. Это необходимо, чтобы новое решение содержало в точности т базисных переменных. (Напомним, что нас интересуют только базисные решения, содержащие в точности т базисных переменных.) В соответст­вии с терминологией симплекс-метода выбранная нулевая переменная называется вводи­мой (в базис), а удаляемая базисная переменная – исключаемой (из базиса).

Пример 1.

Рассмотрим детали выполнения симплекс-метода при решении следующей задачи.

Компания Тиккурила производит краску для внутренних и наружных работ из сырья двух типов: М1 и М2. Основные данные задачи сведены в таблицу.

	Расход сырья (в тоннах) на тонну краски		Максимально возможный ежедневный расход сырья
	Для наружных работ	Для внутренних работ
Сырье М1	6	4	24
Сырье М2	1	2	6
Доход (в $1000) на тонну краски	5	4

Отдел маркетинга компании ограничил ежедневное производство краски для внутренних работ до 2 тонн (из-за отсутствия надлежащего спроса), а также поставил условие, чтобы ежедневное производство краски для внутренних работ не превышало более чем на тонну аналогичный показатель производства краски для внешних работ. Компания хочет определить оптимальное (наилучшее) соотношение между видами выпускаемой продукции для максимизации общего ежедневного дохода.

Переменные задачи:  ₁= объем ежедневного производства краски для наружных работ (тонны),  ₂ = объем ежедневного производства краски для внутренних работ (тонны).

Краска обоих видов производится из сырья М1 и М2. Первые два ограниче­ния задачи порождены ограниченными ежедневными запасами сырья. Другие два отображают ограниченный рыночный спрос на краску. Прибыль от одной тонны краски для наружных работ составляет $5000, а краски для внутренних работ – $4000. Целевая функция задачи должна максимизировать общую при­быль. Для удобства вычислений доходность производства красок масштабирована в тысячах долларов.

Эта задача в стандартной форме записывается так:

максимизировать

при ограничениях

Здесь s₁, s₂, s₃, s₄ – дополнительные (остаточные) переменные, добавленные в неравенства для преобразования их в равенства.

Задачу ЛП в стандартной форме можно представить в виде следующей ком­пактной таблицы.

Нижние четыре строки этой таблицы представляют равенства ограничений; значения правых частей этих равенств даны в столбце "Решение". Строка z = W() полу­чена из равенства

W() – 5 ₁– 4 ₂ = z – 5 ₁– 4 ₂= 0.

Дополнительные переменные s₁, s₂, s₃ и s₄ составляют очевидное начальное допустимое базисное решение. При этом, поскольку небазисные переменные  ₁ и  ₂ равны нулю, значения s₁, s₂, s₃ и s₄ автоматически отображаются в столбце "Решение": s₁ = 24, s₂ ⁼ 6, s₃ = 1 и s₄ = 2. Значение целевой функции при этом решении равно нулю.

Будет ли это начальное решение оптимальным? Конечно, нет, поскольку пере­менные  ₁ и  ₂ здесь равны нулю, а возрастание этих переменных даже на единицу приводит к увеличению значения целевой функции W() = 5 ₁+ 4 ₂ на 5 (при увеличении на единицу  ₁) или на 4 единицы (при увеличении на единицу  ₂). Поскольку в формуле целевой функции коэффициент при переменной  ₁ больше, чем коэффициент при  ₂, переменную  ₁ следует ввести в число базисных переменных (в этом случае она станет вводимой). Если об­ратиться к приведенной выше таблице, то вводимая переменная определяется сре­ди множества небазисных переменных, как переменная, имеющая наибольший по модулю отрицательный коэффициент в z–строке (строке Симплекс разности).

Включаемая (вводимая) переменная  ₁ должна принять положительное значение. На рис. 4.2.1 видно, что, исходя из начальной точки A ( ₁ = 0,  ₂ = 0), наибольшее зна­чение, которое можно присвоить переменной  ₁ (не выходя из пространства до­пустимых решений), равно 4, что соответствует точке B ( ₁ = 4,  ₂ = 0). Это озна­чает, что решение переместилось от крайней точки A в крайнюю точку В.

Рис. 4.2.1

Поскольку симплекс-метод не должен основываться на графическом пред­ставлении задачи ЛП, необходимо определить, как выбрать точку B алгебраиче­ски. Из рисунка 4.2.1 видно, что B является одной из точек пересечения прямых, со­ответствующих ограничениям, с осью  ₁. Алгебраически точку пересечения можно найти как отношение правой части равенства (значение в столбце "Ре­шение") к коэффициенту при переменной ₁ в этом равенстве, как показано в следующей таблице.

Нас интересуют только неотрицательные отношения (или точки пересече­ния на положительной полуоси  ₁), так как они соответствуют направлению возрастания переменной  ₁. Отметим, что все значения в столбце "Решение" неотрицательные, поэтому вычисляемое отношение будет неотрицательным и конечным только в том случае, если знаменатель отношения строго положителен. Именно поэтому мы не рассматриваем отношения, соответствующие третьему и четвертому равенствам, так как там знаменатели или отрицатель­ные, или равны нулю.

Минимальное неотрицательное отношение равно значению вводимой пере­менной  ₁ в новом решении, а именно  ₁= 4 (сравните с точкой B на рис. 1). Зна­чение целевой функции при этом значении  ₁ возрастет до 20 (= 54).

Теперь среди текущих базисных переменных s₁, s₂, s₃ и s₄ следует определить исключаемую переменную, которая примет нулевое значение после введения в базис переменной  ₁. (Напомним, что в этом примере должно быть в точности 4 базисные переменные.) Поскольку наименьшее (неотрицательное) отношение соответствует переменной s₁, в точке B именно эта переменная обращается в нуль. Таким образом, переменная s₁ будет исключаемой, в этом случае переменная  ₁ автоматически получает значение 4. Замена исключае­мой переменной s₁ на вводимую переменную  ₁ приводит к новому базисному решению ( ₁, s₂, s₃, s₄).

Вычисление нового базисного решения основывается на методе исключения переменных (методе Гаусса - Жордана). В следующей таблице, которая пока совпадает с начальной таблицей задачи ЛП, определим ведущий столбец, ассоции­руемый с вводимой переменной, и ведущую строку, ассоциируемую с исключаемой переменной. Элемент, находящийся на пересечении ведущего столбца и ведущей строки, назовем ведущим.

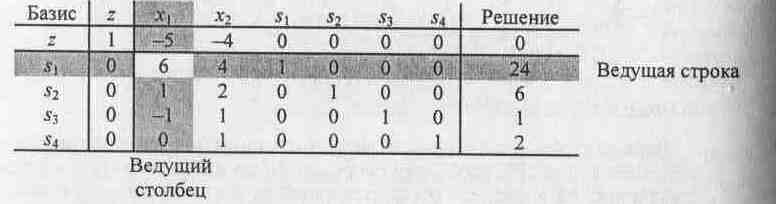
Процесс вычисления нового базисного решения состоит из двух этапов [19]: