Метод множителей Лагранжа для решения задач

нелинейного программирования

с ограничениями в виде равенств

Пусть задача нелинейного программирования поставлена в классической форме:

Минимизировать W = W(Ф) при ограничениях g(Ф) = 0,

где Ф = (₁, ₂, …, _n), g = (g ₁, g ₂, …, g _m)^T.

Описанная процедура составляет основуметода множителей Лагранжа, который позволяет определять стационарные точки задачи оптимизации с ограничениями в виде равенств. Формально схема этого метода представима в следующем виде. Пусть

L(Ф, ) = W(Ф) – g(Ф).

Функция L называется функцией Лагранжа, а параметры  – множителями Лагранжа. Как следует из определения, эти множители имеют тот же смысл, что и коэф­фициенты чувствительности, фигурирующие в методе Якоби. Уравнения

и

дают необходимые условия для определения стационарных точек функции W(Ф) при ог­раничениях g(Ф) = 0. Достаточные условия, используемые в методе множителей Лагран­жа, будут сформулированы без доказательства. Определим матрицу

Н^B =,

где P = 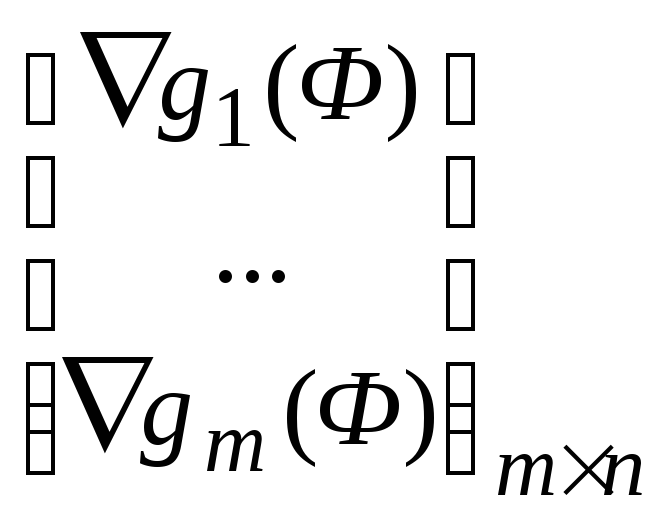иQ = для всехi и j.

Матрица Н^B называется окаймленной матрицей Гессе.

Пусть имеется стационарная точка (Ф⁰, ⁰) функции Лагранжа L(Ф⁰, ⁰) и окаймленная матрица Гессе Н^B вычислена в точке (Ф⁰, ⁰). Тогда Ф⁰ является:

 точкой максимума, если, начиная с главного (углового) минора порядка 2т + 1, последующие п – т угловых миноров окаймленной матрицы Гессе Н^B образуют знакопеременный числовой ряд, в котором знак первого члена определяется множителем (–1)^m+1.

 точкой минимума, если, начиная с главного (углового) минора порядка 2т + 1, последующие п – т главных (угловых) миноров матрицы Н^B имеют знаки, определяемые множителем (–1)^m.

Эти условия являются достаточными для определения экстремальной точки. Другими словами, экстремальной может оказаться стационарная точка, не удовлетворяющая этим условиям.

Существуют другие условия определения экстремальных точек задачи, которые яв­ляются как необходимыми, так и достаточными. Однако их практическое использование часто связано со значительными вычислительными трудностями. Определим матрицу

,

вычисленную в стационарной точке (Ф⁰, ⁰), где  — неизвестный параметр. Пусть |Δ| – определитель матрицы Δ, тогда все п – т действительных корней u_i полинома |Δ| = 0:

 должны быть отрицательными, если Ф⁰ – точка максимума,

 должны быть положительными, если Ф⁰ – точка минимума.

При решении систем уравнений, выражающих необходимые условия экстремума, иногда удобно применять метод, который заключается в последовательном выборе (фиксировании) числовых значений , после чего данная система уравнений решается относительно переменных Ф. Процедура повторяется до тех пор, пока вектор Ф, соответствующий некоторому значению , не будет удовлетворять всем ограничениям.

Пример 4:

Рассмотрим пример решения задачи нелинейного программирования с ограничениями в виде равенств методом множителей Лагранжа при постановке задачи примера 1.

Требуется найти минимум целевой функции: W(Ф) = (₁ – 2)² + (₂ – 1)²,

при ограничениях: g(Ф) = ₁² – ₂ + 2 = 0.

Решение:

1. Найдем значение функции Лагранжа

L(Ф, ) =(₁ – 2)² + (₂ – 1)² –(₁² – ₂ + 2).

2. Продифференцируем функцию Лагранжа по переменным ₁, ₂,  и, приравняв полученные первые частные производные нулю, получим систему уравнений:

3. Решим систему уравнений, выразив из третьего уравнения ₂ через ₁, а из второго –  через ₂, а затем и через ₁:

₂ = ₁² + 2;

 = 2 – 2₂ =2 – 2₁² – 4 = – 2₁² – 2.

Подставив полученное значение  в первое уравнение, получим:

2(1+ 2₁² + 2)₁– 4 = 4₁³+ 6₁ – 4 =₁³+ 1,5₁ – 1=0.

4. Решим неполное кубическое уравнение с помощью формулы Кардано.

Если неполное кубическое уравнение задано в виде:

z³+pz+q=0,

то вещественный корень:

z = , где.

В нашей задаче p = 1,5, а q = – 1.

Тогда  0,6124.

₁⁰==

1,036 + (– 0,482) = 0,554,

тогда ₂⁰ = ₁² + 2 = (0,554)² + 2 = 0,306916 + 2  2,307,

а  = 2– 22,307= – 2,614

Целевая функция в стационарной точке (₁⁰, ₂⁰) принимает значение:

W(₁⁰,₂⁰)= (₁–2)² +(₂–1)²=(0,554–2)² + (2,307–1)² =

= (–1,446)² + (1,307)²2,09+1,7=3,8.

Решением системы уравнений является вектор:

(Ф⁰, ⁰)=( 0,554; 2,307; – 2,614).

5. Построим окаймленную матрицу Гессе Н^B размерностью 33, т. к. n=2, m=1. Элемент матрицы в первом столбце первой строки всегда равен 0, элементы второго и третьего столбца первой строки заполняются первыми частными производными g(Ф) по ₁ и ₂ соответственно. Этими же коэффициентами заполняются элементы первого столбца во второй и третьей строке. Оставшиеся элементы заполняются вторыми производными функции Лагранжа, то есть производными по ₁ (во второй столбец) и ₂ (в третий столбец), взятыми от первых частных производных функции Лагранжа по ₁ (во второй строке) и ₂ (в третьей строке).

Н^B= =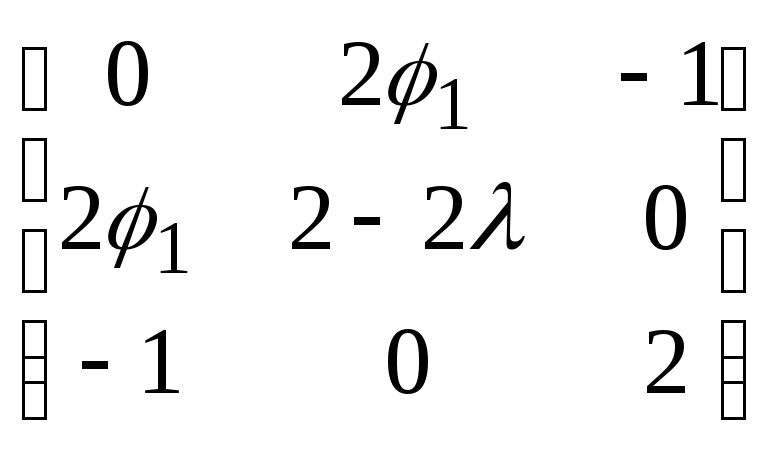, Н^B|_⁰=

6. Используя достаточные условия, вычислим элементы окаймленной матрицы Гессе Н^B. Т. к. n=2, m=1, то для того чтобы стационарная точка была точкой минимума, знак последнего (и единственного) 2 – 1 = 1 главного минора Δ₃ должен определяться знаком множителя (–1)^m =–1 в стационарной точке.

Δ₃ = 0 + 0 + 0 – (–1)  7,228  (–1) – 0 – 2  1,108  1,108  – 9,68.

Т. к. главный минор Δ₃ окаймленной матрицы Гессе Н^B отрицателен, т. е. соответствует достаточным условиям существования в точке Ф⁰=(0,554; 2,307) минимума целевой функции W(Ф) = (₁ – 2)² + (₂ – 1)².