0,48, 1,44,1,44.

Тогда

==0,14,==0,43,==0,43.

Используя модель равномерного сглаживания, вычислим для второго свойства:

4,16, 0,72,0,33.

Тогда

==0,80,==0,14,==0,06.

Используя модель равномерного сглаживания, вычислим для третьего свойства:

0,26, 1,52,2,52.

Тогда

==0,06,==0,35,==0,59.

Значения – сведены в таблицу 2.

Таблица 2

Показатели (языки)	i (свойства)
	1	2	3
	0,14	0,80	0,06
	0,43	0,14	0,35
	0,43	0,06	0,59

Данные значения показывают нормированную степень удовлетворения требованиям к свойствам k₁ – k₃ в каждом из трех языков программирования.

Используя модель равномерного сглаживания, вычислим для важности свойств:

0,30, 0,83,3,98.

Тогда

==0,06,==0,16,==0,78.

Сложная структура задачи выбора, представленная в виде иерархии (рис. 5), приводит к необходимости использования интегрального критерия при определении степени пригодности каждого из трех языков программирования для разработки информационной подсистемы корабельной АСУ: , гдеi – номер альтернативного варианта (языка программирования), j – номер свойства альтернатив (k₁ – k₃).

0,18;

0,32;

0,50.

Таким образом, наиболее предпочтительным для выбора является язык C++. Наименее предпочтительным – язык Visual Basic.

Модели второй группы Модель максимального согласования

Простейшей моделью, относящейся к моделям второй группы, является модель максимального согласования, которая при­меняется для анализа простых структур без равноценных элементов (в матрице только 0 и 1). В данной модели анализируется некоторое упорядочивание I, например упорядочение, определенное порядковыми номерами альтернативных вариантов. Затем это упорядочивание сравнивается с матрицей А, содержащей результаты бинарного сравнения а_ij. Если в I-м упорядочивании i-й элемент предшествует j-му, а в матрице А а_ji =1, то такая ситуация называется минимальным несогласием. В этом случае упорядочивание I корректируется.

Задачей согласования является отыскание такого оптимального упорядочивания I*, чтобы число несогласий было минимально. Графически решение задачи представляется штриховкой правого верхнего угла матрицы А, в котором должны содержаться единичные элементы.

Задачи такого класса относятся к сложным задачам. Их решение сопряжено с решением трудных проблем комбинаторной оптимизации.

Приведем пример, в котором используется интегральный критерий, позволяющий оценить альтернативные варианты по нескольким свойствам или аспектам. Для решения задач линейного упорядо­чивания в этих случаях может быть использован метод идеаль­ной точки.

Метод идеаль­ной точки

Положим, что каждый альтернативный вариант х_i, описыва­ется вектором в пространстве R_n. Определим в этом пространстве идеальную точку а° = (а₁°,..., а_n°). Такая точка оптимальна сразу по всем критериям. Как правило, идеальная точка а° не принадлежит множеству .

Зададим на пространстве R_n расстояние d(а°, х_i), которое вводится аксиоматически: 1). d(а°, х_i)  0; если а°= х_i, то d(а°, х_i) = 0.

2). d(а°, х_i) = d(х_i, а°).

3). d(а°, х_j) + d(х_j, х_i)  d(а°, х_i).

Исходя из этих аксиом, можно ввести различные функции расстояния с общим видом

, где S - целое число.

Если S =2, то получаем евклидово расстояние

Если S =1 имеем .

При S= получим равномерную метрику:

В этом случае лучшей альтернативой является альтернатива, имеющая наименьшее расстояние между значением наихудшего параметра (оценки по критерию) и значением этого параметра для идеальной точки.

Упорядочивание вариантов производится по полученному значению d.

Пусть, например, анализируются четыре альтернативных варианта ЭВМ  = {х₁, х₂, х₃, х₄}. Каждый вариант характери­зуется двумя координатами: емкостью оперативной памяти и тактовой частотой х₁=(4 Мб, 16 МГц); х₂=(8 Мб, 16 МГц); х₃=(4 Мб, 32 МГц); х₄ = (16 Мб, 16 МГц). Тогда идеальной точ­кой будет а°=(16 Мб, 32 МГц). Будем упорядочивать варианты, полагая, что 1 Мб памяти эквивалентен 1 МГц тактовой частоты.

Используя евклидово расстояние, получим:

d(х₁, а°) ==20;

d(х₂, а°)17,9; d(х₃, а°)=12; d(х₄, а°)=16.

Наилучшим в этом случае будет третий вариант. Если использовать равномерную метрику, то наилучшим будет третий вариант, а остальные варианты имеют одинаковое значение d^ и не могут быть упорядочены.

Для метрики d₁: х₃ > х₄ > х₂ > х₁.

Данный пример показывает, что при выборе метрики нужно иметь дополнительную информацию, определяющую важность отстояния критериев от идеальной точки.

Так, выбор равномерной метрики уместен, когда желательно выбрать вариант, значения всех параметров которого незначительно отстоят от наилучшего значения.

Метод "идеальной точки" подразумевает предварительное задание этой точки а° =(а₁°, ..., а_n°). В ряде практических задач определение отдельных координат а_i° идеальной точки не может быть осуществлено однозначно иди с достаточной точностью. В этих случаях производится построение других форм интегральных критериев.

Упражнения:

1. Упорядочить альтернативы, используя модель максимального согласования, если в результате парного сравнения альтернатив получена матрица А, заданная простой структурой без эквивалентных элементов (ПС):

2. Используя модель Ушакова, выбрать одного из трех кандидатов на вакантную должность старшины класса, если в результате их парного сравнения получена матрица А, заданная вероятностной калибровкой:

3. Используя метод анализа иерархий выбрать упорядочить три объекта по степени пригодности для реализации главной цели. Выбранный объект должен в лучшей степени соответствовать трем требованиям, важность каждого из которых для достижения главной цели оценена путем парного сравнения, в результате которого получена матриц А₄, заданная степенной калибровкой (в соответствии с 9-ти бальной шкалой). Результаты парного сравнения альтернатив по соответствию первому, второму и третьему требованию приведены в степенных матрицах А₁ – А₃ соответственно.

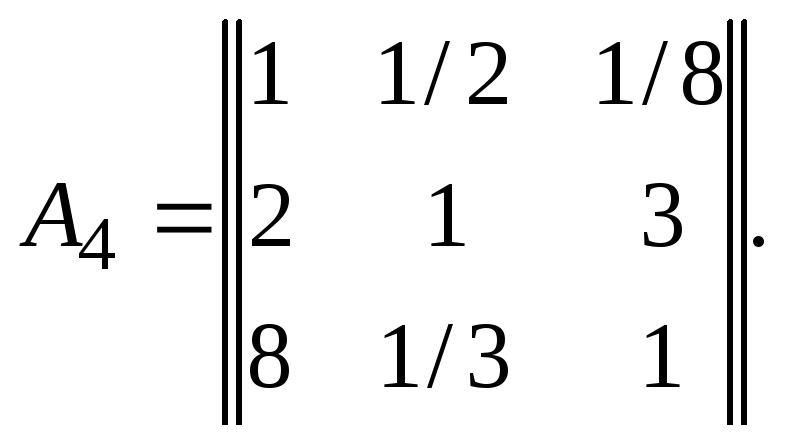
4. Используя равномерную метрику метода идеальной точки упорядочить персональные компьютеры, если каждый компьютер характери­зуется двумя координатами: емкостью оперативной памяти и тактовой частотой х₁=(128 Мб, 2400 МГц); х₂=(256 Мб, 1700 МГц); х₃=(512 Мб, 2000 МГц); х₄ = (256 Мб, 3200 МГц).

Контрольные вопросы:

1. Приведите последовательность действий при принятии решений.

2. Из каких двух этапов состоит процесс формирования множества допустимых альтернатив.

3. Перечислите методы формирования альтернативных вариантов.

4. В чем заключается суть метода мозгового штурма?

5. В чем заключается суть метода круглого стола?

6. В чем заключается суть метода деструктивной оценки?

7. В чем заключается суть метода синектики?

8. В чем заключается суть метода морфологического анализа?

9. В чем заключается суть процедуры экспертного перечисления?

10. Как определяется элемент матрицы парных сравнений при простой структуре?

11. Перечислите способы взвешивания отношений доминирования.

12. Охарактеризуйте турнирную калибровку.

13. Охарактеризуйте степенную калибровку.

14. Охарактеризуйте кососимметричную калибровку.

15. Охарактеризуйте вероятностную калибровку.

16. Охарактеризуйте модели спортивного типа.

17. Охарактеризуйте модель Бредли-Терри.

18. Охарактеризуйте модель Бержа.

19. Охарактеризуйте модель Ушакова.

20. Охарактеризуйте модель равномерного сглаживания.

21. В чем заключается суть метода анализа иерархий?

22. Охарактеризуйте модель максимального согласования.

23. В чем заключается суть метода идеальной точки?