Модель Ушакова

Стохастическая модель Ушакова используется для обработки матриц А, заданных в степенной и вероятностной калибровках. Матрица А преобразуется в вероятностную матрицу Р, произ­вольный элемент которой p_ij интерпретируется как вероятность превосходства x_j над x_i. В том случае, если задана вероят­ностная калибровка, то матрица Р получается из матрицы А путем транспонирования Р = А^Т, т.к. значение a_ij в вероятност­ной калибровке указывает на вероятность того, что i-й вари­ант превосходит j-й.

Так как , то матрицаР преобразуется в матрицу , элемент которой .

Для выполнения условия элементы главной диагонали матрицы : .

В этом случае матрица принимает смысл матрицы вероят­ностей перехода эргодической цепи Маркова, в которой один вариант соответствует одному состоянию. Напомним, что эргодическими называются такие цепи Маркова, у которых вероятности перехода системы в различные состояния (финальные вероятности каждого состояния) перестают ме­няться от шага к шагу, а, следовательно, существуют предельные вероятности перехо­дов в каждое состояние, которые не зависят от исходного состояния. Финальные вероятности каждого состояния определяют значения интегральных пока­зателей _i. Пока­затель _j=. Причем,. В дальнейшем упорядочивание альтернативных вари­антов производится в порядке убывания значений_i.

Рассмотрим пример решения задачи линейного упорядочивания с использованием модели Ушакова для выбора одного из трех кандидатов на вакантную должность командира радиотехнического дивизиона.

В результате их парного сравнения получена матрица А. Затем матрицы Р = А^Т и .

.

Для нахождения финальных вероятностей решим систему ал­гебраических уравнений

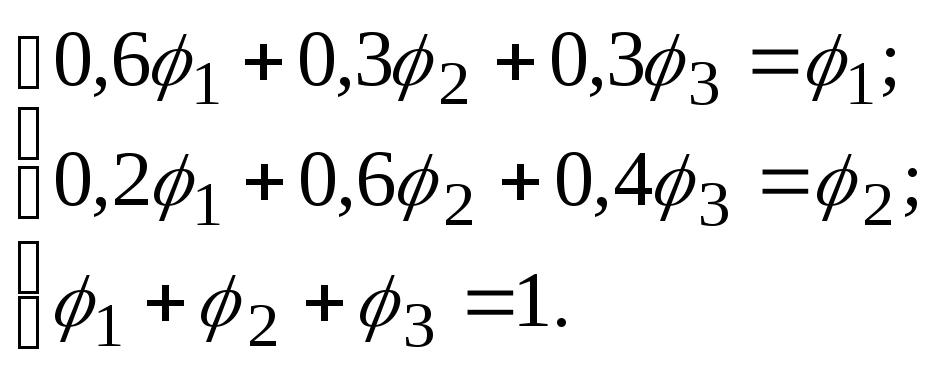
В результате решения системы уравнений получим:

 ₁ = 12/28,  ₂ = = 11/28, ₃ = 5/28.

Следовательно, для замещения вакантной должности командира радиотехнического дивизиона необходимо выбрать первую кандидатуру.

Модель равномерного сглаживания

Модель равномерного сглаживания применяется для обра­ботки матриц А, полученных в результате турнирной или сте­пенной калибровок. При этом устанавливается однозначное со­ответствие между неявно заданными "силами" отдельных вариан­тов. Пусть в степенной калибровке элементы матрицы А a_ij показывают: во сколько раз i-й вариант превосходит j-й вариант. Тогда зависит от .

В этом случае для вычисления интегрального показателя следует опре­делить геометрическое среднее значений в i-й строке матрицы А: . Тогда.

Рассмотрим пример решения задачи линейного упорядочивания с использованием модели равномерного сглаживания с целью выбора языка программирования баз данных для разработки информационной подсистемы корабельной АСУ.

Решение задачи выбора языка программирования в данном примере базируется на методе анализа иерархий, предложенном Т. Саати [14]. Этот метод используется для решения различных практических многокритериальных оптимизационных задач планирования.

Метод анализа иерархий состоит в декомпозиции цели принятия решения на более простые составляющие части (требуемые свойства альтернатив), выявления важности каждого из свойств (аспектов), которыми должна обладать лучшая альтернатива, оценки каждого такого свойства для разных альтернатив и дальнейшей обработке последовательности суждений по парным сравнениям. В результате получается иерархия частных показателей, композиция которых приводит к значениям для каждой из сравниваемых альтернатив.

В методе используется степенная калибровка, которая использует шкалы относительной важности (табл.1). Основу данного метода составляет модель равномерного сглаживания.

Таблица 1

Шкала относительной важности

Интенсивность относительной важности	Определение
1	Равная важность
3	Умеренное превосходство
5	Существенное превосходство
7	Значительное (сильное) превосходство
9	Очень сильное превосходство
2, 4, 6, 8	Промежуточные значения между двумя суждениями

Задача. Требуется выбрать язык программирования баз данных для разработки информационной подсистемы корабельной АСУ. В качестве альтернативных вариантов были предложены три языка: Delphi, C++, Visual Basic.

Декомпозиция задачи выбора языка программирования в ие­рархию представлена на рисунке 5.1.5.

Рис. 5.1.5. Декомпозиция задачи выбора языка программирования

На первом уровне иерархии указана общая цель выбора – выбор языка программирования. На втором уровне находятся три параметра (свойства): k₁ – k₃ , количественно характеризующие качество языков программирования баз данных с точки зрения их выбора для проектирования информационной подсистемы. На третьем уровне иерархии указаны возможные альтернативы.

При построении такой структуры необходимо обеспечить выполнение принципа иерархической непрерывности, состоящего в том, что элементы нижнего уровня должны быть сравнимы по парам по отношению к элементам вышестоящего уровня и т.д. вплоть до вершины иерархии.

Этот принцип позволяет построить иерархию доминирования, в которой альтернативные варианты нижнего уровня относительно (через реализацию свойств) воздействуют на вершину иерархии. Данная декомпозиция строится в результате анализа мнений экспертов. При этом выбранные критерии и альтернативные варианты должны охватывать весь диапазон предпочтений и всю описываемую проблему.

В методе анализа иерархий элементы иерархии сравниваются попарно по отношению к их воздействию на общий для них критерий (свойство), расположенный на предыдущем уровне иерархии.

Решение. Данные сравнения позволяют получить множества степенных матриц А₁ – А₃ для значения свойств k₁ – k₃ в каждом альтернативном языке программирования:

и матрицу А₄ для важности каждого параметра при достижении общей цели:

Используя модель равномерного сглаживания, вычислим для первого свойства: