
- •Глава 1. Уравнения Максвелла 3
- •§2. Ток смещения
- •§3. Закон полного тока с учетом тока смещения
- •§4. Система уравнений Максвелла в интегральной форме
- •§5. Система уравнений Максвелла в дифференциальной форме
- •§6. Волновое уравнение
- •Глава 2. Волны. Поляризация волн §1. Виды волн. Общие свойства волн
- •§2. Плоские монохроматические волны
- •§3. Основные свойства эм-волн
- •§4. Поведение эм-волн на границе раздела двух сред
- •§5. Линзы
- •§8. Получение света с эллиптической или круговой поляризацией
- •§9. Двойное лучепреломление. Способы получения линейно поляризованного света
- •§10. Закон Малюса
- •§11. Степень поляризации света
- •§12. Прохождение светового луча через систему изNполяризаторов с потерями
- •§13. Построение волновых фронтов о- и е-волн и определение направления распространения о- и е-лучей в одноосных кристаллах по Гюйгенсу
- •§14. Длина волны и волновое число при переходе волны из вакуума в среду
- •14.1. Длина волны
- •14.2. Волновое число
- •§15. Фазосдвигающие пластинки. Получение света с произвольной поляризацией
- •§16. Искусственная анизотропия
- •§17. Оптически активные вещества
- •Глава 3. Интерференция волн §1. Основные понятия. Способы получения когерентных световых пучков
- •§2. Количественное описание интерференции. Условия минимумов и максимумов
- •§3. Степень когерентности излучения источника. Интерференция частично когерентных волн
- •§4. Опыт Юнга (деление волнового фронта)
- •§5. Пространственная и временная когерентность излучения источника. Время и длина когерентности
- •§6. Бипризма Френеля
- •§7. Интерференция света на тонких пленках
- •§8. Интерференция света на тонком клине
- •§9. Интерференция света на плоском сферическом клине (кольца Ньютона)
- •Глава 4. Дифракция волн §1. Принципы Гюйгенса и Гюйгенса–Френеля
- •§2. Дифракция волн. Виды дифракции
- •§3. Дифракция Френеля на круглом отверстии
- •§4. Зоны Френеля
- •§5. Дифракция Фраунгофера на щели
- •§6. Дифракционная решетка
- •I(φ) sin φ
- •§7. Угловая и линейная дисперсия. Разрешающая способность
- •Глава 5. Тепловое излучение §1. Определение теплового излучения
- •§2. Поглощательная и излучательная способности тела. Абсолютно черное, белое и серое тела
- •§3. Энергетические характеристики излучения
- •§4. Связь междуrνTиrλT
- •§5. Законы Стефана-Больцмана и Вина
- •§6. Закон Кирхгофа
- •§7. Формула Планка. Доказательство с ее помощью законов Стефана-Больцмана и Вина
- •§8. Излучение серых тел
- •§9. Оптическая пирометрия. Цветовая, яркостная и радиационная температуры
- •Глава 6. Элементы релятивистской механики §1. Релятивистские масса, импульс, энергия
- •§2. Частицы с нулевой массой покоя — фотоны
- •§3. Постулат Эйнштейна о фотонах
- •§4. Волновые и корпускулярные свойства света и микрочастиц. Корпускулярно-волновой дуализм
- •§5. Внешний и внутренний фотоэффект
- •§6. Опытные законы внешнего фотоэффекта
- •§7. Теория фотоэффекта Эйнштейна
- •§8. Давление света
- •§9. Рэлеевское и комптоновское рассеяние света
- •§10. Описание эффекта Комптона
- •§11. Алгоритм решения задач на эффект Комптона
- •Глава 7. Волновые свойства микрочастиц §1. Гипотеза де Бройля. Уравнение волны де Бройля
- •§2. Интерпретация волновой функции
- •§3. Соотношения неопределенностей Гейзенберга
- •§4. Опытное подтверждение гипотезы де Бройля. Опыт Дэввисона и Джермера
- •Глава 8. Уравнение Шредингера §1. Зависящее от времени уравнение Шредингера
- •§2. Стационарное уравнение Шредингера
- •§3. Стандартные условия, налагаемые на волновую функцию
- •§4. Собственные значения и собственные функции оператора Гамильтона. Квантование энергии микрочастиц
- •§5. Смысл волновой функции
- •§6. Простейшая задача квантовой механики: частица в потенциальной яме с бесконечно высокими стенками
§2. Плоские монохроматические волны
Волны вида
![]() (1)
(1)
называют плоскими монохроматическимиилигармоническими. Здесь:
А—амплитудаволны,
![]() —фазаволны,φ—начальная
фаза,x —координата поверхности постоянной фазы
Φ = constв моментt,
—фазаволны,φ—начальная
фаза,x —координата поверхности постоянной фазы
Φ = constв моментt,
![]() —фазовая скоростьволны,
—фазовая скоростьволны,
![]() —циклическая частотаколебаний
в волне,
—циклическая частотаколебаний
в волне,![]() —
частотаколебаний [Гц],T
—период колебаний
в волне,
—
частотаколебаний [Гц],T
—период колебаний
в волне,
![]() —волновое числоилипостоянная
распространения.
—волновое числоилипостоянная
распространения.
Длина волныλ —это путь, проходимый волной за период колебаний:
![]() . (2)
. (2)
Из (2) можно получить для волнового числа
![]() .
.
К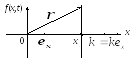 оординатуxповерхности постоянной фазы можно
представить в виде
оординатуxповерхности постоянной фазы можно
представить в виде![]() ,
где
,
где ![]() —
единичный вектор в направлении осиOХ,
—
единичный вектор в направлении осиOХ,
![]() —
радиус-вектор произвольной точки
поверхности постоянной фазы. Тогда
произведениеkxв уравнении волны
можно записать в виде скалярного
произведения, не зависящего от выбора
системы отсчета:
—
радиус-вектор произвольной точки
поверхности постоянной фазы. Тогда
произведениеkxв уравнении волны
можно записать в виде скалярного
произведения, не зависящего от выбора
системы отсчета:
![]() (4)
(4)
где ввели
![]() —волновой вектор.
—волновой вектор.
С учетом этого выражения уравнение плоской волны можно записать в виде
![]() . (5)
. (5)
Часто для монохроматических волн используют комплексное представление, понимая под волной реальную (вещественную) часть комплексной функции
![]() (6)
(6)
где
![]() .
.
Н аряду
с комплексным представлением гармонические
колебания изображают в виде проекции
вектора
аряду
с комплексным представлением гармонические
колебания изображают в виде проекции
вектора
![]() ,вращающегося с угловой скоростьюω,
на осьOX.Начальное положение вектора
,вращающегося с угловой скоростьюω,
на осьOX.Начальное положение вектора
![]() к осиOXсоставляет
уголφ,а произвольное
к осиOXсоставляет
уголφ,а произвольное
![]() ,где
,где![]() отнесено кφ. Проецирование
вектора на осьOХи взятие реальной части комплексного
числа— эквивалентныеоперации.
отнесено кφ. Проецирование
вектора на осьOХи взятие реальной части комплексного
числа— эквивалентныеоперации.
§3. Основные свойства эм-волн
1. ЭМ-волна в среде с εиμраспространяется с фазовой скоростью
![]() , (1)
, (1)
где величина
![]() называетсяабсолютным показателем
преломления среды.
называетсяабсолютным показателем
преломления среды.
2. Векторы
![]() ,
,![]() ,
,![]() в ЭМ-волне взаимно перпендикулярны
и образуют правый винт (правую тройку).
Это внутреннее свойство ЭМ-волны, не
зависящее от выбора системы отсчета.
Так как
в ЭМ-волне взаимно перпендикулярны
и образуют правый винт (правую тройку).
Это внутреннее свойство ЭМ-волны, не
зависящее от выбора системы отсчета.
Так как
![]() и
и
![]() перпендикулярны
перпендикулярны
![]() ,то ЭМ-волныпоперечны.
,то ЭМ-волныпоперечны.

3. Мгновенные значения векторов
![]() и
и![]() в ЭМ-волне связаны соотношением
в ЭМ-волне связаны соотношением![]() ,
откуда с учетом (1)и
,
откуда с учетом (1)и![]() получим
получим
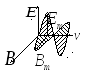
![]() . (2a)
. (2a)
Отсюда следует, что поля
![]() и
и
![]() (
(![]() )
одновременно обращаются в нуль и
одновременно достигают своих максимальных
значений, т.е. колеблютсясинфазно:
)
одновременно обращаются в нуль и
одновременно достигают своих максимальных
значений, т.е. колеблютсясинфазно:
![]() . (2б)
. (2б)
4.ЭМ-волны обладаютобъемной плотностью энергии, мгновенное значение которой с учетом (2а) равно
![]() . (3a)
. (3a)
Cучетом![]() и того, что средние по времени значения
и того, что средние по времени значения
![]() получим для среднего значения
объемной плотности энергии в ЭМ-волне
получим для среднего значения
объемной плотности энергии в ЭМ-волне
![]() . (3б)
. (3б)
5. Через единицу площади в единицу времени ЭМ-волна переносит энергию
![]() . (4а)
. (4а)
Согласно размерности [S]
=Дж/(м2·с) величина S естьплотность потока энергиив волне.
Учитывая, что векторы![]() и
и
![]() в ЭМ-волне взаимно перпендикулярны (4а)
можно записать в виде
в ЭМ-волне взаимно перпендикулярны (4а)
можно записать в виде
![]() . (4б)
. (4б)
Вектор
![]() называютвектором Пойнтинга(вектором
Умова,вектором Умова-Пойнтинга).
Он указывает направление переноса
энергии в волне. Среднее по времени
значение вектора Умова-Пойнтинга
называютинтенсивностью волны
называютвектором Пойнтинга(вектором
Умова,вектором Умова-Пойнтинга).
Он указывает направление переноса
энергии в волне. Среднее по времени
значение вектора Умова-Пойнтинга
называютинтенсивностью волны
![]() (5a)
(5a)
С учетом (1) и (2б), (4а)
![]() . (5б)
. (5б)
6. ЭМ-волна с энергией Wобладает импульсом
![]() (6a)
(6a)
Плотность импульса волны(импульс единицы объема волны) равна
![]() , (6б)
, (6б)
где учтено, что S=wυиw=S/υ.
7. Волна оказывает на частично отражающую поверхность давление
![]() , (7)
, (7)
где
![]() —интенсивность волны,R— коэффициент отражения. Для абсолютно
поглощающей поверхностиR=0,для зеркалаR=1.
—интенсивность волны,R— коэффициент отражения. Для абсолютно
поглощающей поверхностиR=0,для зеркалаR=1.
8. Согласно Эйнштейну ЭМ-волна есть поток корпускул(фотонов).ЭнергияW,импульсKи масса волныmпо Эйнштейну равны
W=mc2, K=mc=W/c; m=W/c2=K/c, (8)
где WиKмогут быть рассчитаны электродинамически (см. выше). Энергия одного фотона согласно гипотезе Эйнштейна равнаε=hν,гдеh — постоянная Планка,ν —частота волны.
9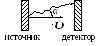 .Если источник, испускающий волну частотыν0,и приемник ЭМ-излучения (света) движутся
относительно друг друга со скоростьюυ,то частотаνизлучения,
регистрируемая приемником (детектором)
излучения изменяется и равна
ν=ν0(1
υcos
α/c). (9)
.Если источник, испускающий волну частотыν0,и приемник ЭМ-излучения (света) движутся
относительно друг друга со скоростьюυ,то частотаνизлучения,
регистрируемая приемником (детектором)
излучения изменяется и равна
ν=ν0(1
υcos
α/c). (9)
Это явление называют эффектом Доплера. Здесь α —угол между направлением скорости источникаυи направлением испускания волны,c —скорость света. Знак «+» — сближение источника и детектора, знак «−» — их удаление друг от друга.
