6.6. Указания по обработке результатов и содержанию отчета

1. По результатам измерений построить график зависимости тока диода от напряжения смещения (вольт-амперную характеристику). Для каждой пары значений ток — напряжение указать на графике доверительные интервалы.

2. Из графика найти значения U_max, U_min иI_max. Оценить доверительную погрешность этих результатов.

3. По полученным результатам U_max, U_min иI_maxоценить положение уровня Ферми, максимума плотности распределения электронов в зоне проводимости, вероятность туннелирования электронов черезр–n-переход. Экспериментальные результаты сравнить с результатами предварительных расчетов.

4. Сформулировать выводы по работе.

Список литературы

1. Савельев И. В. Курс общей физики. — М.: Наука. 1979, т. 3, § 26, 52—53.

2. Пасынков В. В., Чиркин Л. К., Шинков А. Д. Полупроводниковые приборы. — М.: Высшая школа, 1966, гл. 4.

3. Справочник по полупроводниковым диодам, транзисторам и интегральным схемам. / Под ред. Н. Н. Горюнова.—М.: Энергия, 1976.

4. Методические указания к курсу лекций по физике (Твердое тело), / Сост. Г. Ф. Холуяиов, Б. Ф. Алексеев. — Л.: ЛЭТИ, 1982.

Работа 7. Компьютерное моделирование туннельного эффекта

Цель работы: Ознакомление с компьютерным экспериментом на примере исследования эффекта туннелирования и надбарьерного отражения микрочастицы.

Приборы и принадлежности: Персональный компьютер, оснащенный интерактивной программой для решения одномерного стационарного уравнения Шредингера.

Общие сведения: Для описания движения микрочастиц используется аппарат квантовой механики. Состояние микрочастицы в квантовой механике задается волновой функцией, аргументами которой являются координатыи время. Квадрат модуля волновой функциихарактеризуетобъёмнуюплотность вероятности обнаружения частицы:, где– вероятность обнаружения частицы в элементарном объеме, находящимся в точке с координатамив момент времени. Вероятность нахождения частицы в конечном объемеопределяется интегралом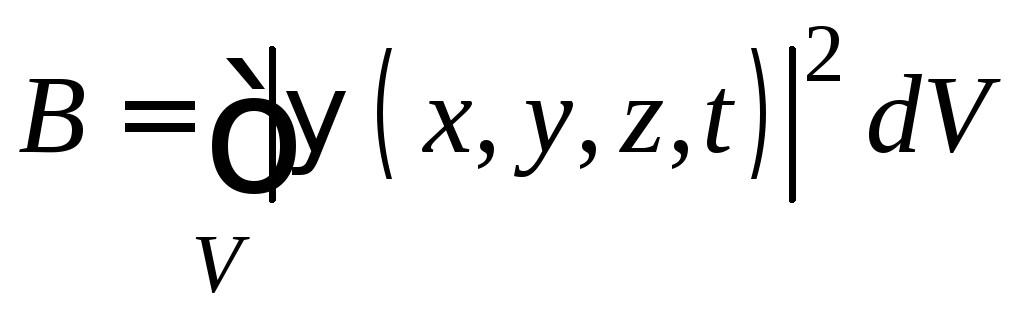. В предельном случаезначение, согласно условию нормировки-функции, асимптотически приближается к единице.

Определение типа волновой функции производится с помощью уравнения Шредингера. Если потенциальная энергия не зависит от времени (стационарное состояние квантово-механической системы) и зависит только от одной координаты, то уравнение Шредингера принимает вид:

, (7.1)

где – масса движущейся частицы,– энергия частицы,– потенциальная энергия, характеризующая взаимодействие частицы с окружающими объектами.Решения уравнения (7.1)должны удовлетворять стандартным условиям: волновая функция и её производные конечны и не имеют разрывов во всех точках пространства.

Для повышения точности решения уравнения Шредингера численным методом необходимо записать (7.1) в виде соотношения, содержащего безразмерные величины:

, (7.2)

где – относительная координата;– боровский радиус электрона в атоме водорода;– относительная энергия частицы;– энергия основного состояния электрона в атоме водорода;– относительная масса частицы;– масса покоя электрона;– относительная энергия взаимодействия частицы с окружающими объектами.

Моделируемые закономерности

При движении частицы в однородном потенциальном поле вероятность её обнаружения в любой точке пространства одинакова. В неоднородном полеусловие постоянстване выполняется.

Рассмотрим движение частицы вдоль оси в потенциальном полеописываемом функцией, обычно называемойпрямоугольнымпотенциальным барьером (рис. 7.1 а):

а) б) в) I II III

Рис. 7.1. Графики потенциальной функции (а) и реальной части функциипри(б) и(в).

,

где – ширина барьера в относительных единицах. Волновая функция частицы с энергиейв каждой из областей пространства (I,II,III), имеет вид

(7.3)

Слагаемые в правой части (7.3), содержащие коэффициенты , описывают движение частицы слева направо, слагаемые содержащие коэффициенты– движение частицы в обратном направлении. Отметим, что коэффициентопределяет вероятность обнаружения частицы в областиIIIпри ее движении из областиI, а коэффициент­– вероятность возврата частицы в областьI. Из условия непрерывности функциии её производнойв точках иследует система линейных уравнений (7.4), содержащих неизвестные коэффициенты.

(7.4)

Из решения системы (7.4) возникают соотношения, связывающие искомые коэффициенты с энергией частицы, высотойи ширинойбарьера.

Вероятность проникновения частицы из области Iв областьIIIпринято характеризоватькоэффициентом прохождения , а вероятность возврата частицы в областьI– коэффициентом отражения . Коэффициентыиудовлетворяют условиюи определяются соотношениями:

, .(7.5)

Если >, то с точки зрения классической механики частица не может перейти из областиIв областьII. Однако квантовая механика прогнозирует конечную вероятность проникновения (туннелирования) частицы из областиIв областьIII. Точное аналитическое выражение для коэффициентаимеет сложный вид, поэтому для оценок используют более простое эмпирическое соотношение:

. (7.6)

В случае барьера треугольной формы (рис. 5.2) коэффициент прохождения оценивают также с помощью эмпирического соотношения:

(7.7)

Если энергия частицы больше высоты барьера (<), то согласно законам классической механики частица беспрепятственно проходит из областиIв областьIII. Однако квантово-механическое решение обнаруживает конечную вероятность того, что частица вернется (надбарьерное отражение) в областьI. При>показатель экспоненты в (7.3) становится мнимым и волновая функцияявляется осциллирующей функцией (рис.7.1,в). Коэффициент отраженияпринимает минимальныеи максимальныезначения (рис. 7.3) в зависимости от энергии частицыи ширины барьера:

(7.8)

где – целочисленный параметр.

Рис. 7.2. Потенциальный барьер треугольной формы	Рис. 7.3. Зависимость коэффициента отражения от энергии частицы в случае