Черкозьянов А. Т., доц. к. т. н

ИНЖЕНЕРНАЯ ГЕОДЕЗИЯ

Конспект лекции

Специальность 290300 - «Промышленное и гражданское строительство»

Форма обучения	Дневная	Вечерняя	Заочная
Курс	1	1	1
Семестр	2	2	2
Лекции	17	17	8
Практические занятия	34	17	10
Лабораторные занятия	-	-	-
Всего аудиторных занятий	51	34	18
Самостоятельная работа	49	66	82
РГР (количество)	2	2	2 к. раб.
Экзамен (семестр)	2	2	2

2008. г.

-2 –

ОСНОВЫ ГЕОДЕЗИИ

ВВЕДЕНИЕ

Предмет и задачи геодезии. Задачи инженерной геодезии в строительстве

Определение геодезии как науки об измерениях на земной поверхности, математической обработки результатов измерений и оценки их точности.

Задачи геодезии: определение формы и размеров Земли и ее внешнего гравитационного поля – основная научная задача; построение опорной геодезической сети на всей территории страны – основная научно-техническая задача; картографирование земной поверхности (карты и планы); обеспечение геодезическими данными всех видов строительства.

Научные дисциплины геодезии: высшая геодезия; физическая геодезия; космическая геодезия; радиогеодезия; аэрофотогеодезия; картография; топография; инженерная геодезия.

Задачи инженерной геодезии. 1) На стадии инженерно-строительных изысканий: составление топографических планов строительных участков; составление продольных профилей линейных сооружений; согласование вопросов по отводу земель, обеспечению строительства электроэнергией, водой, газом и т.п. 2) На стадии проектирования: составление плана вертикальной планировки (расчет картограммы земляных работ); подготовка данных для переноса проекта на местность (составление разбивочного плана); построение разбивочной основы. 3) На стадии строительства: разбивка и закрепление на местности основных, промежуточных и монтажных осей; вынос проектных отметок на монтажные горизонты; контроль геометрической точности строительно-монтажных работ; исполнительные съемки. 4) На стадии эксплуатации: определение деформаций инженерных сооружений.

Геодезические измерения и приборы.

Геодезические измерения: угловые, линейные, высотные (нивелирование).

Измерения технической точности: угловые - 15″-30″; линейные – 1/1000-1/5000; нивелирование – 10 мм на 1 км хода.

Точные измерения: угловые - 2″-5″; линейные – 1/10000-1/ 100000; нивелирование – 3 мм на 1 км хода.

Высокоточные измерения: угловые – 0.5″-1″; линейные – 1/100000-1/500000; нивелирование – 0.5 мм на 1 км нивелирного хода.

Геодезические приборы. Для угловых измерений: теодолиты Т30, Т15 и их модификации - технической точности; теодолиты Т5, Т2 и их модификации – точные. Для линейных измерений: сталь- ные рулетки, ленты, дальномеры- технической точности; инварные рулетки, светодальномеры – технической точности. Для нивелиро -вания: нивелиры Н10 – технической точности; нивелиры Н3 – точ-ные; нивелиры Н0,5 – высокоточные. Основные координатные оси, относительно которых ведутся измерения, рис.1: отвесная линия (направление силы тяжести), горизонтальная линия. Приборы для их построения: отвес, уровни.

Единицы измерений

Градус – центральный угол соответствующий 1/360 части окружности, 1º=60', 1'=60" (по Герону, 6 век до н. э.). Угловая единица по Герону в настоящее время входит в международную систему измерений (СИ). Связь с радианом: в одном радиане число градусов ρº=180/π=57.2958º (π=3.1416), число минут ρ'= ρº* 60=3438', число секунд ρ"= ρ'* 60=206265". Гон (раньше град) – центральный угол соответствующий 1/400 части окружности, 1G=100C (одинарных секунд), 1С=100СС (двойных секунд). Число гонов в одном радиане ρG = 200G / π. Применяется в

Угловые. Радиан – центральный угол, соответствующий дуге окружности равной радиусу, рис.2: φ^рад = s / R (s = φ^рад R, R =s /φ^рад по этой формуле определен радиус земного шара в 230 г. до н. э. Эратосфеном).

.

-3 -

современных теодолитах Германского производства для упрощения вычислений угловых измерений на микрокалькуляторе (МК). Например, отсчет по теодолиту 34^G85^C65^CC будет соответствовать 34,8565^G – удобно для вычислений. По отечественному теодолиту Т2 отчет 34º36'36" будет соответствовать 34+(36+36/60)/60=34,61º для ввода в МК. Или, по теодолиту Т5 отсчет 34º 36.6'= 34,61º.

Линейные измерения: метр – одна сорока миллионная дуги Парижского меридиана, принятая на международной конференции в Париже в 1792 г. Входит в СИ в настоящее время.

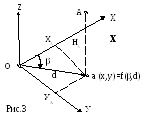Математическая обработка и оценка точности геодезических измерений

В геодезии важны функции результатов измерений. Например, положение точки в пространстве в заданной системе координат и высот: точка А(х, у, Н) = f (угловых, линейных, высотных измерений), рис.3. Вычисление координат и высот производится по формулам тригонометрии. До разработки микрокалькуляторов (МК) математическая обработка результатов измерений велась с применением 5-ти - 6-ти значащих таблиц тригонометрических функций (четырехзначные таблицы Брадиса в геодезии не применяются) и арифмометра. В настоящее время вычисления ведутся на МК или ЭВМ.

На МК три программы: DEG - для вычислений в градусах, RAD - в радианах, GRAD - в гонах. На ЭВМ вычисления ведутся по специально разработанным программам. Программы записаны на дискеты, хранятся на кафедре ТОС.

Любое измерение абсолютно точно не выполнить. Речь может вестись только о степени приближения к истинному значению. Поэтому кроме результата измерения l должна указываться степень доверия к нему. В основу оценки точности результатов измерений положена теория способа наименьших квадратов Гаусса. Критерием точности измерений по Гауссу является средняя квадратическая погрешность (m). Она входит в шифр геодезического прибора. Например теодолит Т30 - m =30”, теодолит Т5 - m = 5”, нивелир Н3 - m =3 мм на 1 км хода.

m – средняя погрешность, вероятность которой 67% (из 100 измерений 67 содержат погрешности более m). В строительных нормах и правилах (СНиП) устанавливаются предельные погрешности равные 3m. Измерения, погрешности которых превышают 3m, бракуются.