Тема 1. Общие сведения о фигуре Земли, координатах и об ориентировании линий

1.1. Фигура Земли

Земля – геоид: тело ограниченное уровенной поверхностью моря.

Уровенная поверхность – поверхность перпендикулярная направлениям сил тяжести в каждой точке (или поверхность равного потенциала сил тяжести)

Уровенная поверхность, совпадающая с поверхностью мирового океана, принимается за основную - поверхность геоида.

Направления сил тяжести являются функцией плотности земной коры. А так как распределение масс в земной коре неравномерно, то и изменение направлений сил тяжести также неравномерно. Вследствие этого поверхность геоида становится сложной и неправильной в геометрическом отношении, что ее форму нельзя описать математическим уравнением. Вести обработку результатов измерений на поверхности, которая не описывается математической формулой , невозможно.

Наиболее близко к поверхности геоида подходит поверхность эллипсоида вращения (земного сфероида),параметры которого являютсябольшая полуосьа и полярное сжатие  = ( а – в ) / а , гдев – малая полуось, рис. 1.1.

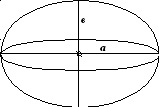
Рис. 1.1. Элементы земного сфероида

В разное время ученые многих стран занимались определением параметров земного сфероида, в том числе советские ученые Ф. Н. Красовский и А. А. Изотов. По их данным а = 6 378 245 м,  = 1 / 298.3, получившего название«эллипсоид Красовского».С 1946 г. вся обработка геодезических измерений в нашей стране ведется на его поверхности.

Для решения многих задач прикладного значения Землю принимают за шар радиуса R = 6 371.11км, равновеликого по объему «эллипсоиду Красовского». В приближенных расчетах R = 6371 км.

1.2. Системы координат

С и с т е м а г е о г р а ф и ч е с к и х к о о р д и н а т. В этой системе Землю принимают за шар, а за координатные оси – географические (истинные) меридианы и параллели. Начало координат – пересечение Гринвичского меридиана, принимаемого за ноль, с экватором. Точка на поверхности шара определяется географической широтойВи географической долготойL. ( Долгота 0⁰– центр зала Гринвичской обсерватории вблизи Лондона). Географические координаты подписаны на топографических картах.

С и с т е м а п л о с к и х п р я м о у г о л ь н ы х к о о р д и н а т применяется на небольших участках ( до 20 х 20 км ), принимаемых за плоскость. Ось Х – северное направление меридиана, ось У – восточное направление горизонтальной линии, рис.1.2.

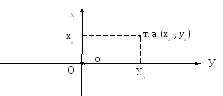
Рис. 1. 2. Плоские прямоугольные координаты

В строительстве эта система применяется для составления планов небольших участков . Начало координат т. О выбирается с таким расчетом, чтобы на всем плане не было отрицательных координат (план должен располагаться в северо-восточной части).

С и с т е м а п о л я р н ы х к о о р д и н а т. В строительстве эта система, рис.1.3, применяется при съемочных работах. За полюс Опринимают точку местности, за полярную осьОА- любое направление на местности; т.Мбудет описываться координатами: полярным углом, измеренным от полярной оси по часовой стрелке, и полярным расстояниемd. ТочкуМлегко построить на плане при помощи транспортира и линейки.

Рис. 1.3. Полярная система координат

С и с т е м а п л о с к и х п р я м о у г о л ь н ы х к о о р д и н а т

Г а у с с а - К р ю г е р а

Система применяется для изображения на плоскости значительных частей земной поверхности с учетом кривизны Земли. Для этой цели земную поверхность делят с севера на юг на узкие ленты – зонышириной 6⁰. На экваторе ширина зоны около 667 км, к северу – уменьшается. Счет зон от Гринвичского меридиана на восток. Средний меридиан зоны называетсяосевым, долготу его L₀можно подсчитать по формуле

L₀ = 6 n – 3⁰ ,(1.1)

где n- номер зоны.

Каждая зона (от 1 до 60) в отдельности проектируется на плоскость при условии равенства углов на сфере и на плоскости. Такая проекция называется равноугольнойи обеспечивает подобие контуров на сфере и на плоскости, что удобно при решении задач в строительстве. При развертывании зоны в плоскость экватор и осевой меридиан изображаются прямыми линиями, которые принимаются за координатные оси:ось х – северное направлениеосевого меридиана, ось у – восточное направление экватора, рис.1.4.

Точка на местности обозначается координатами:n, x, y– номер зоны, расстояния от экватора и осевого меридиана. Например, т.В: зона 3,х = 6 021 550 м, у = - 205 675 м. Такая система называетсядействительнойсистемой координат.

Рис.1.4. Система координат Гаусса – Крюгера

В действительной системе точки, расположенные к востоку от осевого меридиана зоны, имеют положительные ординаты, к западу - отрицательные. Для удобства чтения все ординаты на картах увеличены на 500 км. Связь между измененными ординатами и действительными:

у' = y + 500 000 м. (1.2)

Перед измененной ординатой пишется номер зоны. Такие ординаты называются преобразованными.Например, по карте определили: т В: х = 6 021 550 м, у(преобр.) = 3 294 325м. Следовательно, зона 3, действительная ордината в соответствии с (1.2)у= - 205 675м. Или,у (пр.) = 32 675 450 м., что соответствует зоне 32, расстоянию от осевого меридиана зоныу = + 175 450 м.

Для удобства определения координат точек на планах и картах строят координатные сетки - линии параллельные координатным осям. На картах они кратны км (километровая сетка). На планах проводятся через 1 см. При решении задач по определению координат точек по картам и планам измерения ведутся циркулем-измерителем до 0.2 мм от двух координатных линий сетки. За окончательный результат берут среднее. Измерения от двух линий, как для х так и для у повышают точность измерений, компенсируют деформацию бумаги, выявляют грубые ошибки.

С и с т е м ы в ы с о т. Высоты, отсчитанные от уровенной поверхности моря (поверхности геоида), называютсяабсолютными. В нашей стране за абсолютный нуль принят многолетний средний уровень Балтийского моря, рис. 1.5.

Такая система высот называется Балтийской. Разность высот точек называетсяпревышением

h_АВ = Н_В – Н_А - (1.3)

превышение по линии АВ. Превышение по линииВА (обратное)h_ВА = Н_А -Н_В ; очевидно, чтоh_ВА = - h_АВ.

.

Рис. 1.5. Системы высот

1- уровенная поверхность Балтийского моря; 2 – физическая земная поверхность; 3 – отвесные линии; Н_{А ,} Н_В – высоты в Балтийской системе; h_АВ – превышение точки В над точкой А

Высоты, отсчитанные от произвольной уровенной поверхности, называются условными(илиотносительными). Такую систему высот принято называтьчастной(илиместной). В строительстве преимущественно применяется частная система высот. Так при возведении отдельных зданий и сооружений за нуль высот принимают верхнюю поверхность пола первого этажа жилого дома или пола цеха промышленного предприятия. Эту отметку выносят на цоколь здания и от нее ведут отсчет: вверх - с плюсом, вниз - с минусом. Численное значение высоты называетсяотметкой.