
Лекции / Лекция 7
.docxЛекция 7
1.Протокол OSPF. 2.Управление соединением и потоком. 3.Промежуточные состояния соединения. 5. Трансляция сетевых адресов NAT.
Протокол OSPF
Протокол маршрутизации OSFP (Open Shortest Path First) представляет собой протокол состояния связей, использующий алгоритм SPF поиска кратчайшего пути в графе. OSPF применяется для внутренней маршрутизации в системах сетей любой сложности.
Пример OSPF-системы
Обозначения на рисунке: Ѓ, ‚, ѓ, „ – маршрутизаторы; A, B, C, D – линии связи (или просто связи), цифры означают метрику каждой связи.
Метрики
Метрика представляет собой оценку качества связи в данной сети (на данном физическом канале); чем меньше метрика, тем лучше качество соединения. Метрика маршрута равна сумме метрик всех связей (сетей), входящих в маршрут. В простейшем случае (как это имеет место в протоколе RIP) метрика каждой сети равна единице, а метрика маршрута тогда просто является его длиной в хопах.
Поскольку при работе алгоритма SPF ситуации, приводящие к счету до бесконечности, отсутствуют, значения метрик могут варьироваться в широком диапазоне. Кроме того, протокол OSPF позволяет определить для любой сети различные значения метрик в зависимости от типа сервиса. (Тип сервиса запрашивается дейтаграммой в соответствии со значением поля TOS ее заголовка, см. п. 2.4.) Для каждого типа сервиса будет вычисляться свой маршрут, и дейтаграммы, затребовавшие наиболее скоростной канал, могут быть отправлены по одному маршруту, а затребовавшие наименее дорогостоящий канал – по другому.
Метрика сети, оценивающая пропускную способность, определяется как количество секунд, требуемое для передачи 100 Мбит через физическую среду данной сети. Например, метрика сети на базе 10Base-T Ethernet равна 10, а метрика выделенной линии 56 кбит/с равна 1785. Метрика канала со скоростью передачи данных 100 Мбит/с и выше равна единице.
Порядок расчета метрик, оценивающих надежность, задержку и стоимость, не определен. Администратор, желающий поддерживать маршрутизацию по этим типам сервисов, должен сам назначить разумные и согласованные метрики по этим параметрам.
Если не требуется маршрутизация с учетом типа сервиса (или маршрутизатор ее не поддерживает), используется метрика по умолчанию, равная метрике по пропускной способности.
В нашем примере мы будем использовать метрики, указанные на рисунке, без учета типов сервиса. Следует заметить, что маршрутизация по типам сервиса крайне редка, более того, она исключена из последних версий стандарта OSPF
База данных состояния связей
Для работы алгоритма SPF на каждом маршрутизаторе строится база данных состояния связей, представляющая собой полное описание графа OSPF-системы. При этом вершинами графа являются маршрутизаторы, а ребрами – соединяющие их связи. Базы данных на всех маршрутизаторах идентичны.
За создание баз данных и поддержку их взаимной синхронизации при изменениях в структуре системы сетей отвечают другие алгоритмы, содержащиеся в протоколе OSPF. Мы рассмотрим эти алгоритмы позже, а сейчас будем считать, что базы данных на всех маршрутизаторах каким-то образом построены, синхронизированы и правильно описывают граф системы в данный момент времени.
База данных состояния связей представляет собой таблицу, где для каждой пары смежных вершин графа (маршрутизаторов) указано ребро (связь), их соединяющее, и метрика этого ребра. Граф считается ориентированным, то есть ребро, соединяющее вершину Ѓ с вершиной ‚, и ребро, соединяющее вершину ‚ с вершиной Ѓ, могут быть различны или это может быть одно и то же ребро, но с разными метриками.
База данных состояния связей в нашем примере (см. рис. 5.1.1) выглядит следующим образом:
|
|||||||||||||||||||||||||||
|
|
Алгоритм SPF
Алгоритм SPF, основываясь на базе данных состояния связей, вычисляет кратчайшие пути между заданной вершиной S графа и всеми остальными вершинами. Результатом работы алгоритма является таблица, где для каждой вершины V графа указан список ребер, соединяющих заданную вершину S с вершиной V по кратчайшему пути.
Алгоритм SPF был предложен Е.В.Дейкстрой (E.W.Dijkstra).
Пусть
S – заданная вершина (источник путей);
E – множество обработанных вершин, то есть вершин, кратчайший путь к которым уже найден;
R – множество оставшихся вершин графа (то есть множество вершин графа за вычетом множества E);
O – упорядоченный список путей.
Описание алгоритма
1. Инициализировать E={S}, R={все вершины графа, кроме S}. Поместить в О все односегментные (длиной в одно ребро) пути, начинающиеся из S, отсортировав их в порядке возрастания метрик.
2. Если О пуст или первый путь в О имеет бесконечную метрику, то отметить все вершины в R как недостижимые и закончить работу алгоритма.
3. Рассмотрим P – кратчайший путь в списке О. Удалить P из О. Пусть V – последний узел в P.
Если VÍE, перейти на шаг 2;
иначе P является кратчайшим путем из S в V (будем записывать как V:P); перенести V из R в E.
4. Построить набор новых путей, подлежащих рассмотрению, путем добавления к пути P всех односегментных путей, начинающихся из V. Метрика каждого нового пути равна сумме метрики P и метрики соответствующего односегментного отрезка, начинающегося из V. Добавить новые пути в упорядоченный список О, поместив их на места в соответствии со значениями метрик. Перейти на шаг 2.
Все вычисления производятся локально по известной базе данных, а потому – быстро по сравнению с дистанционно-векторными протоколами, при этом результаты получаются на основе полной, а не частичной информации о графе системы сетей
Пример работы алгоритма SPF
Рассмотрим работу алгоритма на примере базы данных состояния связей рассматриваемой системы (рис. 5.1.2).
|
Отадо |
Сеть |
Метрика |
|
Ѓа‚ |
A |
2 |
|
Ѓаѓ |
C |
3 |
|
Ѓа„ |
B |
1 |
|
‚аЃ |
A |
2 |
|
ѓаЃ |
C |
3 |
|
ѓа„ |
D |
1 |
|
„аЃ |
B |
1 |
|
„аѓ |
D |
1 |
Возьмем в качестве вершины S маршрутизатор ѓ.
Инициализация
S=ѓ, E={ѓ}, R={Ѓ,‚,„}, O={D,C} (из вершины ѓ согласно базе данных выходят только связи D (к „) и С (к Ѓ), причем метрика D меньше).
Итерация 1
P=D. Поскольку D ведет от ѓ к „, то V=„. Так как V не находится в Е, то кратчайший путь ѓа„ есть P. Добавляем этот факт в таблицу результатов, изымаем P из O, переносим V из R в Е.
Строим новые пути (шаг 4 алгоритма): согласно базе данных из вершины V=„ существует два односегментных пути: B и D. Добавив их к P=D, получим пути DD и DB с метрикой 2 каждый. Эти пути добавляются в упорядоченный список О.
E={ѓ,„}, R={Ѓ,‚}, O={DD,DB,C}.
Результаты: („: D)
Итерация 2
P=DD. Двигаясь по этому пути из ѓ, мы попадем опять в ѓ, то есть V=ѓ. Так как V находится в Е, то исключаем P из О и переходим к следующей итерации.
E={ѓ,„}, R={Ѓ,‚}, O={DB,C}.
Результаты: („: D)
Итерация 3
P=DB. Двигаясь по этому пути из ѓ, мы попадем в Ѓ, то есть V=Ѓ. Так как V не находится в Е, то кратчайший путь ѓаЃ есть P. Добавляем этот факт в таблицу результатов, изымаем P из O, переносим V из R в Е.
Строим новые пути: согласно базе данных из V=Ѓ существует три односегментных пути: A,В и C. Добавив их к P=DB, получим пути DBA, DBB и DBC с метриками 4,3 и 5 соответственно. Эти пути добавляются в упорядоченный список О.
E={ѓ,„,Ѓ}, R={‚}, O={C, DBB, DBA, DBC}.
Результаты: („: D;Ѓ:DB)
Итерация 4
P=С. V=Ѓ. Так как V находится в Е, то исключаем P из О и переходим к следующей итерации.
E={ѓ,„,Ѓ}, R={‚}, O={DBB, DBA, DBC}.
Результаты: („: D;Ѓ:DB)
Итерация 5
P=DBB. V=„. Так как V находится в Е, то исключаем P из О и переходим к следующей итерации.
E={ѓ,„,Ѓ}, R={‚}, O={DBA, DBC}.
Результаты: („: D;Ѓ:DB)
Итерация 6
P=DBA, следовательно V=‚. Так как V не находится в Е, то кратчайший путь ѓа‚ есть P. Добавляем этот факт в таблицу результатов, изымаем P из O, переносим V из R в Е.
Строим новые пути: согласно базе данных из V=‚ существует один односегментный путь A. Добавив его к P=DBА, получим путь DBAА с метрикой 6. Этот путь добавляется в упорядоченный список О.
E={ѓ,„,Ѓ,‚}, R={}, O={DBC,DBAA}.
Результаты: („: D;Ѓ:DB,‚:DBA)
Итерации 7 и 8
На этих итерациях из списка О будут удалены оставшиеся пути, так как они ведут к вершинам, уже находящимся в множестве Е, больше никаких изменений не произойдет.
Итерация 9
Так как список О пуст и множество R пусто, то кратчайшие пути из S до всех вершин графа построены, недостижимых вершин нет. Работа алгоритма закончена.
Результатом работы является таблица кратчайших путей от маршрутизатора ѓ до всех остальных маршрутизаторов:
ѓаЃ:DB
ѓа‚:DBA
ѓа„:D
На основе этой информации в узле ѓ строится таблица маршрутов, ведущих ко всем узлам OSPF-системы. Для этого из вышеприведенной таблицы нужно взять первую связь каждого пути. Маршрутизатор, к которому ведет эта связь, будет являться следующим маршрутизатором для данного маршрута. При этом алгоритм SPF гарантирует, что и следующий маршрутизатор построил кратчайшие пути, соответствующие путям маршрутизатора ѓ, то есть если кратчайший путь из ѓ в ‚ (DBA) лежит через узел „, в который ведет связь D, то кратчайший путь из „ в ‚ будет ВА.
Таким образом, таблица маршрутов в узле ѓ будет выглядеть:
ѓаЃ: через „, линия D
ѓа‚: через „, линия D
ѓа„: через линию D
Разграничение хостов и маршрутизаторов
Выше мы разбирали систему сетей, состоящую только из маршрутизаторов, соединенных двухточечными линиями связи. В этой системе отсутствовали хосты.
Предположим, что к маршрутизатору „ подключена сеть N1 из некоторого количества хостов H1-Hk (см. рис. 5.1.3). Следуя разобранной выше модели, каждый хост должен быть также вершиной графа OSPF-системы, хотя сам и не строит базу данных и не производит вычисления маршрутов. Тем не менее, информация о связях маршрутизатора „ с каждым из хостов сети N1 и о метриках этих связей должна быть внесена в базу данных, чтобы все остальные маршрутизаторы системы могли построить маршруты от себя до этих хостов.

Рис. 5.1.3. OSPF-система с маршрутизаторами и хостами
Очевидно, что такая процедура неэффективна. Вместо информации о связях с каждым хостом в базу данных вносится информация о связи с сетью, то есть сама IP-сеть становится вершиной графа системы, соединенной с маршрутизатором „ с помощью некоторой связи P (см. рис. 5.1.4).
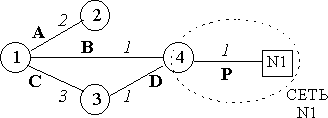
Рис. 5.1.4. OSPF-система с маршрутизаторами и тупиковой сетью
Подчеркнем, что в данном случае сеть, точнее ее адрес, используется как обобщающий идентификатор группы хостов, находящихся в одной IP-сети, к которой маршрутизатор „ непосредственно подключен. Вершина N1 называется тупиковой сетью (stub network); все узлы сети, обозначаемые этой вершиной, являются хостами, у которых установлен маршрут по умолчанию, направленный на маршрутизатор „.
Протокол OSPF производит разграничение хостов и маршрутизаторов. Если к IP-сети N1 подключен еще и один из интерфейсов маршрутизатора ‚, то связь между ‚ и „ будет установлена отдельно, как если бы они были соединены двухточечной линией связи (при этом у маршрутизатора ‚ также будет связь с тупиковой сетью N1).
При подключении тупиковой сети N1 в базе данных состояния связей появится запись:
|
Отадо |
Связь |
Метрика |
|
„аN1 |
P |
1 |
Связей, направленных из вершины N1, в базе данных не будет, потому что вершина N1 не является маршрутизатором. Построение маршрутов до вершины N1 (то есть фактически сразу до всех хоcтов сети N1) будет произведено каждым маршрутизатором обычным способом по алгоритму SPF.
