
mat_mod_bilety_posled_var_1
.pdf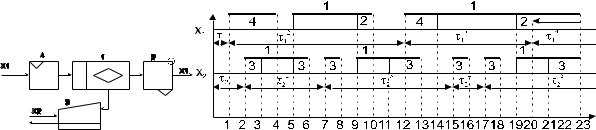
12 вопрос. Имитационное моделирование систем (имитация функционирования системы).
Предположим, исследуется вычислительная система (ВС), состоящая из процессора 1 с основной памятью, устройство вода перфокарт 4, АЦПУ 2 и дисплея 3 (рис. 4.1.).Рис. 4.1. Упрощённая схема моделируемой системы.
Через устройство 4 поступает поток заданий Х1. Процессор обрабатывает задания и результаты выдаёт на АЦПУ 2. Одновременно с этим ВС используется, например, как информационно-справочная система. Оператор-пользователь, работающий за дисплеем, посылает в систему запросы Х2, которые обрабатываются процессором и ответы выводятся на экран дисплея. Процессор работает в 2-х программном режиме: в одном разделе обрабатываются задания Х1, в другом, с более высоким относительным приоритетом запросы Х2. Представим данную ВС в упрощённом варианте в виде стохастической сети из 4-х СМО. Потоки заданий и запросы будем называть потоками заявок. Считаем потоки Х1 и Х2 независимыми. Известны ф.р. периодов следования заявок 1 и 2 и длительность обслуживания Т1К , T2К заявок в к-ом устройстве. Требуется определить времена загрузки каждого устройства и времена реакции по каждому из потоков.
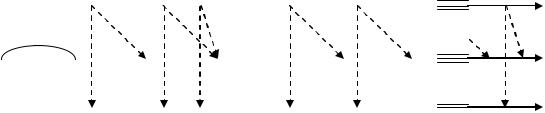
Вначале определяется момент поступления в систему 1-ой заявки потока Х1 по результатам случайного испытания в соответствии с ф.р. периода следования заявок.На рис. 2 это момент времени t1=0+ 11 (здесь и далее верхний индекс обозначает порядковый номер заявки данного потока). То же самое делается для потока Х2. На рис.2 момент поступления 1-ой заявки потока Х2t2=0+ 21. Затем находится минимальное время, т.е. наиболее раннее событие. В примере это время t1. Для 1-ой заявки потока Х1определяется время обслуживания устройством ввода перфокарт Т114 методом случайного испытания и отмечается момент окончания обслуживания t4=t1+ Т114. На рис. показан переход устройства 4 в состояние "занято". Одновременно определяется момент поступления следующей заявки потока Х1: t12=t1+ 12. Следующее минимальное время это момент поступления заявки потока Х2 - t2. Для этой заявки находится время обслуживания на дисплее Т123 и отслеживается время окончания обслуживания t3=t2+ Т123 . Определяется момент поступления второй заявки потока Х2: t7=t2+ 22 . Снова выбирается минимальное время — это t3. В этот момент заявка потока Х2 начинает обрабатываться процессором. По результату случайного испытания определяется время её обслуживания T121 и отмечается момент t5=t3+ T121 окончания обслуживания. Следующее минимальное время t4 - момент завершения обслуживания заявки потока Х1 устройством 4. С этого момента заявка может начать обрабатываться процессором, но он занят обслуживанием потока Х2. Тогда заявка потока Х1 переходит в состояние ожидания, становиться в очередь. В следующий момент времени t5 освобождается процессор. С этого момента процессор начинает обрабатывать заявку потока Х1, а заявка потока Х2 переходит на обслуживание дисплеем, т.е. ответ на запрос пользователя передаётся из основной памяти в буферный накопитель дисплея. Далее определяются соответствующие времена обслуживания: T111 и T123 и отмечаются моменты времени t9=t5+ T111 и t6=t5+ T123. В момент t6 полностью завершается обработка первой заявки потока Х2. По разности времени t6 и t2 вычисляется время реакции по этой заявке u12= t6- t2. Следующий минимальный момент t7 - это наступление 2-ой заявки потока Х2. Определяет время поступления очередной заявки этого потока t15= t7+ 23. Затем вычисляется время обслуживания 2-ой заявки на дисплее T223 и отмечается момент t8=t7+ T223, после чего заявка становится в очередь, т.к. процессор занят. Эта заявка поступит на обслуживание в процессор только после его освобождения в момент t9 . В этот момент заявка потока Х1 начинает обслуживаться в АЦПУ. Определяются времена обслуживания Т221 и Т112 по результатам случайных испытаний и отмечаются моменты окончания обслуживания t11= t9+Т223 и t10= t9+Т112. В момент времени t10 завершается полное обслуживание 1-ой заявки потока Х1. Разность между этим моментом и моментом времени t1 даёт 1-ое значение времени реакции по потоку Х1u11= t10- t1.
Указанные процедуры выполняются до истечения времени моделирования. В результате получается некоторое количество (выборка) случайных значений времени реакции (u1) и (u2) по 1-ому и 2-ому потокам. По этим значениям могут быть определены эмпирические функции распределения и вычислены количественные вероятностные характеристики времени реакции. В процессе моделирования можно суммировать продолжительности занятости каждого устройства обслуживанием всех потоков. Например, на рис. 2 занятость процессора 1 выделена заштрихованными ступеньками. Если результаты суммирования разделить на время моделирования, то получатся коэффициенты загрузки устройств.
Можно определить время ожидания заявок в очереди, обслуженных системой, среднюю и максимальную длину очереди заявок к каждому устройству, требуемая ёмкость памяти и др.
Имитация даёт возможность учесть надёжностные характеристики ВС. В частности, если известны времена наработки на отказ и восстановления всех входящих в систему устройств, то определяются моменты возникновения отказов устройств в период моделирования и моменты восстановления. Если устройство отказало, то возможны решения:
снятие заявки без возврата;
помещение заявки в очередь и дообслуживание после восстановления;
поступление на повторное обслуживание из очереди;
13 вопрос. Обобщённые алгоритмы имитационного моделирования (алгоритм моделирования по принципу особых состояний).
Оно использовалось в приведённом выше примере. В качестве событий выделены:
поступление заявки в систему;
освобождение элемента после обслуживания заявки;
завершения моделирования;
возникновение отказа устройств |
(другие-типы |
|
завершение восстановления устройств |
событий) |
|
|
Процесс имитации развивался с использованием управляющих |
|
|
последовательностей, определяемых по функциям распределения |
|
|
вероятностей исходных данных путём проведения случайных испытаний. В |
|
|
качестве управляющих последовательностей использовались в примере |
|
|
последовательности значений периодов следования заявок по каждому i- |
|
|
ому потоку { i} и длительности обслуживания заявок i-ого потока |
|
|
устройством {Tik}. Моменты наступления будущих событий определялись |
|
|
по простым рекуррентным соотношениям. Эта особенность даёт |
|
|
возможность построить простой циклический алгоритм моделирования, |
|
|
который сводится к следующим действиям: |
|
|
1) |
определяется событие с минимальным временем — наиболее |
|
раннее событие; |
|
|
2) |
модельному времени присваивается значение времени |
|
наступления наиболее раннего события; |
|
|
3) |
определяется тип наступившего события; |
|
4) |
в зависимости от типа события предпринимаются действия, |
|
направленные на загрузку устройств и продвижение заявок в соответствии |
|
|
с алгоритмом их обработки, и вычисляются моменты наступления будущих |
|
|
событий; эти действия называют реакцией модели на события; |
|
|
5) |
перечисленные действия повторяются до истечения времени |
|
моделирования. |
|
|
В процессе |
моделирования производится измерение и статистическая |
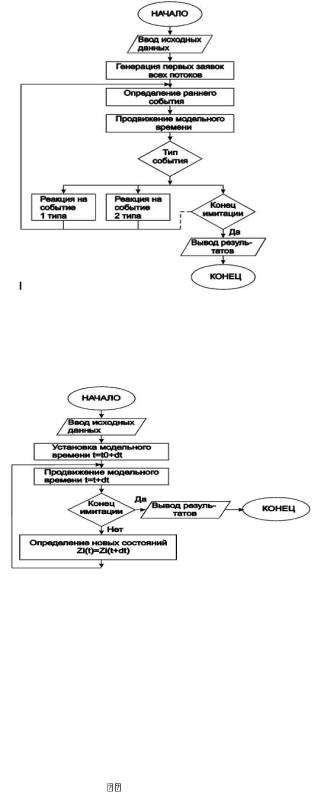
обработка значений выходных характеристик. Обобщённая схема алгоритма моделирования по принципу особых состояний приведена на рисунке 5.1.
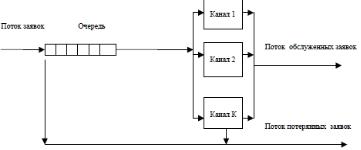
14 вопрос. Обобщённые алгоритмы имитационного моделирования (алгоритм моделирования по принципу t).
1) Устанавливаются начальные значения (состояния) t=0
2) Задаетсяприращениемодельноговремени
3) На основе вектора текущих состояний элементов модели и нового времени мы рассчитываем новые значения этих состояний
4) Если не превышено время моделирования, то три предыдущих этапа повторяются.
Моделирующий алгоритм, основанный на применении dt применим для более широкого круга систем, чем алгоритм, построенный по принципу особых состояний. Однако при его реализации возникают проблемы определения величины dt. Для моделирования ВС на системном уровне в основном используются принцип особых состояний.
15 вопрос. Марковские процессы. Марковские цепи. (в конспекте)
Марковским называется случайный процесс, состояние которого в очередной момент времени зависит только от текущего состояния и не зависитот предыстории процесса. В классе марковских процессов выделяют процессы с дискретными состояниями, называемые марковскими цепями. Когдамножество состояний процесса S = {s1…sk} конечно, марковская цепь называется конечной. Конечная марковская цепь может быть определена в непрерывном или дискретном времени. В первом случае переходы процесса из одного состояния в другое связываются с произвольными моментами времениt0, t1, t2… и цепь называют непрерывной; во втором переходы идут только вфиксированные моменты времени, обозначаемые порядковыми номерами t =0, 1, 2, .., и цепь называется дискретной.Дискретнаямарковская цепь определяется :1) множеством состояний S = {s1,…,sk};2) матрицей вероятностей переходов (или переходных вероятностей), характеризующей вероятности перехода процесса с текущим состоянием siвследующее состояние sj;3) вектором начальных вероятностей P = {p1,..pk}, определяющим вероятность рiтого, что в начальный момент времени t = 0 процесс находится всостоянии si.Марковские цепи классифицируются в зависимости от возможностиперехода из одних состояний в другие. Основными являются два класса: поглощающие и эргодические цепи.Поглощающая марковская цепь содержит поглощающее состояние,достигнув которого процесс уже никогда его не покидает, по сути дела этомоделирует прекращение процесса. Из какого бы состояния ни начался процесс, при n→ с вероятностью 1 он окажется поглощающем состоянии s0.Основная характеристика процесса, порождаемого поглощающеймарковской цепью, - число пребывания процесса в состояниях s1,…,skдомомента поглощения. Поглощающие марковские цепи используются вкачестве моделей программ. При моделировании программы состояния цепиотождествляются с блоками программы, а матрица переходных вероятностейопределяет порядок переходов между блоками, зависящий от структурыпрограммы и распределения исходных данных, значения которых влияют на развитие вычислительного процесса. В результате удается вычислить числообращений к блокам программы и время
выполнения программы.Аналогично можно представить и работу с аппаратурной частью, когдасостояния отображают
использование отдельных устройств компьютера.Эргодическая (возвратная) марковская цепь представляет собоймножество состояний, связанных матрицей переходных вероятностей такимобразом, что из какого бы состояния процесс ни исходил, после некоторогочисла шагов он может оказаться в любом состоянии, в том числе и исходном.Процесс, порожденный эргодической цепью, начавшись в некотором состоянии, никогда не завершается, а последовательно переходит из одногосостояния в другое, попадая в различные
состояния с разной частотой,зависящей от переходных вероятностей. Поэтому основная характеристикаэргодической цепи – вероятности пребывания процесса в состояниях s1,…,sk.Эргодические цепи используются в качестве моделей надежности систем.При этом состояния системы, различающиеся составом исправного иотказавшего оборудования, трактуются как состояния эргодической цепи, переходы между которыми связаны с отказами и восстановлениямиустройств и реконфигурацией связей между неми,
проводимой длясохранения работоспособности системы в целом. Оценки характеристикэргодической цепи дают представление о надежности поведения системы.Кроме того, эргодические цепи используются в качестве базовых моделейвзаимодействия устройств с задачами, поступающими на обработку.Марковский процесс, в котором переходы между состояниями разрешаются в любой момент времени, называется непрерывной марковской цепью. Однородная непрерывная марковская цепь, поведение которой в любоймомент времени подчиняется одному и тому же закону, задается матрицейинтенсивности переходов Q = [qij]; i,j= 1….K.Интенсивность переходов определяется следующим образом:
( |
) |
|
где рi,j( t) – вероятность перехода процесса из состояния siв состояние sjзавремя t.Вероятность перехода процесса |
( |
) |
|
|
|
|
в любое новое состояние равна –qi,j t.Основная характеристика непрерывной марковской цепи – стационарное (финальное) распределение вероятностей состоянийА= {a1,….ak}, где ai– вероятность пребывания процесса в состоянии si.
16 вопрос.Компоненты и классификация моделей массового обслуживания.
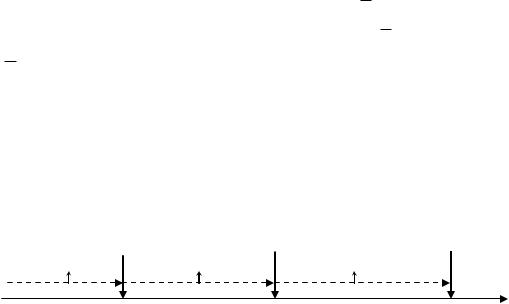
В теории массового обслуживания изучаются системы, на вход которых поступает случайный поток заявок (требований), приходящихся в общемслучае на случайные моменты времени. Поступившая заявка обслуживаетсяв системе путем предоставления ей некоторых ресурсов на какое-то время и,будучи в той или иной мере обслуженной, покидает систему. Наиболее характерный момент функционирования систем массового обслуживания – этоналичие очередей, в которых заявки ждут момента освобождения ресурсов,занятых обслуживанием других заявок.В простейшем случае система массового обслуживания (СМО) определяется потоком заявок, длиной очереди и дисциплиной обслуживания (порядком выбора заявок из очереди), числом каналов (приборов)
обслуживания, распределением длительности обслуживания. В более сложных случаяхрассматривается надежность приборов обслуживания. Структура многоканальной однофазной СМО приведена на рис. 5.1.Число мест в очереди – это число заявок, которые могут ожидать обслуживания, находясь в СМО. По ограничению очереди СМО разделяются насистемы с нулевой длиной очереди, на системы с конечной (определенной)длиной очереди и системы с неограниченной длиной очереди. В системах снулевой и конечной длиной очереди имеют место отказы. Заявка,попавшая на отказ, считается потерянной.Рис. 5.1.Дисциплина очереди может быть без приоритетов или с приоритетами.Таким образом, СМО характеризуется следующим наборомпараметров:1)
распределением длительности интервалов между заявками входящего потока р(а);2) числом мест в очереди;3) дисциплиной обслуживания заявок D;4) числом обслуживающих приборов (каналов) K;5) распределение длительности обслуживания заявок приборами p(b);6) надежностью обслуживающих приборов.Указанный набор параметров полностью определяет порядок функционирования системы. Процесс функционирования количественно оценивается следующим набором основных характеристик:1) загрузкой – средним по времени числом приборов, занятых обслуживанием;2) длиной очереди – средним числом заявок, ожидающих обслуживания;3) числом заявок, находящихся в системе (в очереди и на приборах);4) временем ожидания – средним временем пребывания заявок в очереди;5) временем пребывания заявки в системе;6) временем исправной работы приборов;7) количеством обслуженных и потерянных заявок.В многофазных СМО очереди могут быть на каждой фазе обслуживания. В тех случаях, когда возможно возвращение заявки после обслуживанияна последующей фазе к обслуживанию на одной из предшествующих, говорят о более сложных образованиях - сетях массового обслуживания. Сетьмассового обслуживания можно представить как совокупность узлов – отдельных СМО. Сеть массового обслуживания задается следующим наборомпараметров:1) параметрами источника заявок;2) структурой, определяющей конфигурацию связей и вероятности передачизаявок между узлами сети;3) параметрами СМО, образующих сеть.Функционирование сети массового обслуживания определяется совокупностью узловых и сетевых характеристик. Узловые характеристики оценивают работу каждой СМО и включают в себя весь набор их характеристик.Сетевые характеристики оценивают функционирование сети в целом и включают в себя:1) загрузку – среднее по времени число заявок, обслуживаемых сетью исреднее число каналов, занятых обслуживанием;2) число заявок, ожидающих обслуживания в сети;3) число заявок, находящихся в сети в состоянии обслуживания или ожидания;4) суммарное время ожидания заявки в сети;5) суммарное время пребывания заявки в сети.
17 вопрос.Имитационное моделирование систем массового обслуживания (общие положения).
Одним из методов исследования сложных систем, в том числе, и систем массового обслуживания (СМО) является метод имитационного моделирования, когда модель (как следует из названия вида моделирования) имитирует работу реальной системы, т.е. модель воспроизводит процесс функционирования реальной системы во времени.
Любая система, как известно, представляет собой совокупность взаимосвязанных элементов и, следовательно, построение ее адекватной имитационной модели предполагает имитацию процесса функционирования каждого отдельного элемента системы с обязательным сохранением логики и правил взаимодействия и развития составляющих систему элементов, как во времени, так и в пространстве (в том числе последовательность и параллелизм их во времени).
Основное преимущество имитационного моделирования перед другими видами моделирования (например, аналитическим) состоит в универсальности в смысле возможности исследования любых достаточно сложных систем, с учетом таких факторов и условий, которые трудно или вообще невозможно учитывать при аналитическом моделировании. Поэтому во многих
случаях имитационное моделирование становится наиболее эффективным, а часто и практически единственно доступным методом исследования систем. При исследовании систем со стохастическим характером функционирования (СМО являются системами такого типа) результаты, полученные при единичном "прогоне" имитационной модели (при единичном воспроизведении на имитационной модели процесса функционирования системы), носят частный характер. Следовательно, для того, чтобы найти одну оценку (одно значение) какой-либо характеристики функционирования системы необходимо многократно "прогонять" имитационную модель (необходимо получить множество результатов) с последующей статистической обработкой полученных данных. Поэтому в имитационной модели должны быть предусмотрены средства сбора и средства последующей статистической обработки данных, полученных в ходе моделирования по интересующим характеристикам системы. Например, моделирование случайной величины Y, распределенной по экспоненциальному закону
F( y ) 1 e |
t |
с параметром |
, предполагает выполнение следующих действий:1) розыгрыш равномерно |
|
|
||||
распределенного |
случайного числа x [0, ];2) определение соответствующего значения |
y F 1( x ) ln x / |
||
.Единичная реализация этой элементарной имитационной модели из двух действий дает одно значение случайной величины
Y. Если задача (цель) моделирования состоит в оценке среднего значения Y , то необходимо добавить в модель дополнительное (третье) действие S = S + y для накопления суммы случайных величин (средство сбора) и многократно
реализовать полученную модель. В конце моделирования в качестве оценки для Y принять отношение S/N (средство обработки), где N – общее число реализаций модели.Если необходимо построить (найти) функциональную зависимость
среднего значения Y , например, от параметра , то для множества точек этой зависимости нужно проделать каждый раз всю описанную выше процедуру моделирования, сбора и обработки данных. Даже в такой простой задаче очевидным образом проявляется присущий имитационному моделированию недостаток — это его трудоемкость.
18 вопрос. Имитационное моделирование систем массового обслуживания (действия и события в системах).
Процесс функционирования системы — это последовательная смена состояний системы во времени или другими словами, процесс функционирования системы — это переход ее из одного состояния в другое. Причина перехода системы из состояния в состояние называется событием, которое является, в свою очередь, следствием начала или окончания соответствующего действия. Рассмотрим действия и события, имеющие место в системах на примере СМО типа G/G/1, где под состоянием системы понимается число заявок k, находящихся в ней в данный момент времени. Хронологическая последовательность действий и событий, имеющих место в общем случае в такой СМО при прохождении через систему одной заявки (одного элемента), представлена на рис.2.1.Как видно из рис.2.1 не все события, возникающие в системе, являются равнозначными в
Действия:
События:
Состояния:
"Поступление" |
"Ожидание" |
"Обслуживание" |
||
|
|
|
|
tM |
"Прибытие (приход) заявки" |
"Начало обслуживания" |
"Окончание обслуживания" |
||
"Начало ожидания" |
|
|
"Занятие прибора" |
"Освобождение прибора" |
"Присоединение к очереди" |
|
"Уход из очереди" |
"Уход из системы" |
|
k k +1 |
|
|
Нет изменений |
j j – 1 |
том смысле, что не все события приводят к изменению состояния системы. Исходя из этого, различают два вида событий:1) основные (особые) события;2) вспомогательные (второстепенные) события. Основным событием называется событие, наступление которого приводит к изменению состояния системы.Именно основное событие имелось в виду при определении события как причины перехода системы из одного состояния в другое. Очень часто при имитационном моделировании дается другое определение основного события как события, время наступления которого можно планировать (предсказать) заранее, т.е. рассчитать его можно до фактического возникновения события.
Любое событие, не являющееся основным, называется вспомогательным (второстепенным). Вспомогательные события являются следствием возникновения основных событий и, следовательно, зависимы от них и наступают тогда же, когда и основные.Основные события всегда "связаны" с независимыми временными параметрами, необходимыми или задаваемыми для описания системы.Для рассматриваемой нами системы G/G/1 такими параметрами являются интервалы поступления и длительности обслуживания заявок. Очевидно, что по истечении интервала поступления и длительности обслуживания наступают соответственно события "прибытие заявки" и "окончание обслуживания". Именно эти два события и являются основными в рассматриваемой системе, и появление их вызывает очевидные переходы системы из состояния в состояние. Все другие события на рис.2.1 являются вспомогательными. Так, события "начало обслуживания" и "занятие прибора" являются следствием наступления либо события "приход заявки" (если система свободна), либо события "окончание обслуживания" (для предыдущей заявки). В свою очередь, события "освобождение прибора" и "уход из системы" являются следствием возникновения события "окончание обслуживания".Ни одно вспомогательное событие, очевидно, не приводит к изменению состояния системы. Таким образом, процесс функционирования системы, будучи процессом перехода из состояния в состояние, можно представить как упорядоченную во времени последовательность основных событий, происходящих в системе и переводящих ее из одного состояния в другое. Для поддержания этой хронологической последовательности основных событий в модели используется время.
19 вопрос. Имитационное моделирование систем массового обслуживания (модельное время).
Имитационное моделирование, как правило, проводится с использованием средств вычислительной техники в соответствии с программой, реализующей последовательность возникающих в системе основных событий, т.е. соответствующий процесс функционирования системы. При этом несколько часов, суток, лет работы реальной системы моделируется за несколько секунд, минут, часов работы компьютера.При имитационном моделировании различают три вида времени.
1.Время реальной системы — это время, в котором "живет", функционирует моделируемая система.
2.Модельное время — это "искусственное" время, в котором "живет" модель или другими словами это время, которое является имитацией, прообразом (моделью) времени реальной системы.
3.Реальное время — это время, в котором живет исследователь, компьютер или другими словами это время необходимое для
моделирования (затратное время).
Для нас наибольший интерес представляет модельное время. Для того, чтобы вести отсчет модельного времени и обеспечить правильную хронологическую последовательность наступления основных событий в имитационной модели используется так называемый таймер модельного времени, которая представляет собой переменную для хранения (фиксации) текущего значения модельного времени.В процессе моделирования системы, таймер модельного времени, безусловно, должен постоянно корректироваться в соответствии с теми основными событиями, которые возникают в реальной системе. При этом существуют два способа (два принципа) коррекции значения таймера модельного времени:
1)коррекция с постоянным шагом (принцип t);
2)коррекция с переменным шагом (принцип z).
В первом случае при каждой коррекции модельное время увеличивается на одно и то же значение t, выбираемое перед началом моделирования, а во втором случае значение приращения таймера каждый раз является случайной, а, значит, переменной величиной. Проиллюстрируем оба принципа коррекции таймера на примере. Пусть С1, С2, С3, ... – основные события, происходящие в системе, а t1, t2, t3,...- моменты появления этих событий. Отметим эти события и соответствующие моменты на оси времени реальной системы, причем полагаем, что события С4 и С5 происходят одновременно (рис.3.1, а) Рис. 3.1. Моменты возникновения и обработки событий.В модели, где время корректируется с постоянным шагом по принципу t (рис.3.1, б) модельное время tM будет последовательно принимать значения t1' = t,t2' = 2 t, t3' = 3 t и т.д. Эти
a) |
|
|
С1 |
С2 |
С3 |
С4С5 |
С6 |
|
Ск |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
t1 |
t2 |
t3 |
t4t5 |
t6 |
|
tк |
|
|
ts |
||
|
|
|
|
|
|||||||||
0 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
С0 |
|
|
б) |
|
|
|
|
|
|
|
|
|
tк' |
Т tM |
||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
0 |
t1' |
t2' |
t3' |
t4' |
t5' |
t6' |
|||||||
в) |
|
|
|
|
|
|
|
|
|
|
С0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tM |
|
|
|
|
|
|
t4'' t5'' |
|
|
|
|
|
|||
0 |
|
t1'' |
t2'' t3'' |
|
t6'' |
|
t '' |
Т |
|||||
|
|
|
|
|
|
|
|
|
|
к |
|
||
моменты модельного времени никак не связаны с моментами t1, t2, t3... появления событий в реальной системе. При этом подходе после очередного приращения таймера на величину t проверяется, не произошли ли на этом интервале в системе какие-нибудь события. Если есть такие события, то они обрабатываются, считая, что они якобы произошли в текущий момент модельного времени (правая граница интервала приращения), хотя реально события появились в другие моменты времени из интервала t. Очевидно, что при этом обработка событий может производиться группами. Выбор значения t оказывает существенное влияние на результаты моделирования с точки зрения адекватности отражения реальных событий в модели и затрат ресурсов компьютера на моделирование.В модели, где время корректируется с переменным шагом или по принципу z, значения, принимаемые модельным временем, совпадают, а значит, непосредственно связаны с моментами возникновения событий в реальной системе: t1" =t1, t2" =t2, t3" =t3. Достигается это тем, что при очередном приращении (после отработки события в текущий момент времени) модельное время сдвигается вперед до момента наступления следующего (ближайшего по времени) события. Отсюда, каждый раз модельное время получает переменное приращение, равное интервалу между двумя последовательными основными событиями. Очевидно, что при таком подходе, события отрабатываются в той последовательности, в те моменты времени, в которые они возникают в реальной системе. При этом одновременная обработка событий в модели имеет место только тогда, когда эти события появляются одновременно и в реальной системе (события С5 и С6 на рис.3.1).Для реализации способа завершения моделирования по выполнению
условия tM Т с тем, чтобы при каждой коррекции таймера не проверять выполнение этого условия, в модель можно ввести основное псевдо-событие "окончание моделирования". Такое событие укладывается в концепцию основных событий как событий, которых можно планировать заранее, т.к. момент наступления события "окончание моделирования" задается заранее в начале моделирования.На рис. 3.1. введенное псевдо-событие обозначено через С0с моментом наступления Т. Если после очередной коррекции модельного времени выяснится, что наступило событие "окончания моделирования", то принимается соответствующее решение.
20 вопрос. Имитационное моделирование систем массового обслуживания (логическая схема имитационной модели).
Используя изложенные выше положения, разработаем обобщенную логическую схему имитационной модели простейшей СМО типа G/G/1, которую затем, зная стандартные процедурные языки программирования, можно реализовать на компьютере. Разработку схемы будем вести при следующих условиях.
1.Заданы функции распределения A(t) и B(t) для интервалов поступления и длительностей обслуживания заявок, т.е. СМО полностью формализована.
2.В системе соблюдается условие существования стационарного режима, т.е. условие, что загрузка =b/a< 0, где а и b – средние значения соответственно интервалов поступления и длительностей обслуживания.
3.В начале моделирования система свободна.
4.Задано время моделированияТ и в общем случае, когда моделирование завершается, система может быть не
свободна.
5.Дисциплиной обслуживания является дисциплина FIFO.
6.В результате моделирования определяются следующие характеристики функционирования СМО:
а) загрузка системы ; б) среднее время ожидания ;
в) средняя длина очереди l;
г) среднее время пребывания u;
д) среднее число заявок в системе m; е) максимальная длина очереди Nqmax.
4.1. Планирование основных событийДля рассматриваемой системы G/G/1, как отмечалось ранее, основными событиями являются события "прибытие заявки" и "окончание обслуживания", которые "связаны" соответственно с интервалом
поступления и длительностью обслуживания заявки. Ранее также отмечалось, что основные события можно планировать заранее. Что означает это утверждение?
Суть этого утверждения состоит в том, что:
а) зная функцию распределения A(t) интервалов поступления, при имитационном моделировании в момент прихода очередной заявки можно определить момент поступления следующей заявки;
б) аналогично, зная функцию распределенияВ(t) длительностей обслуживания, при имитационном моделировании в момент начала обслуживания заявки можно определить момент его окончания.Время прибытия следующей заявки, таким образом, определяется, причем точно. Получается, что модель каждый раз в момент прихода очередной заявки узнает, когда появится следующая заявка, хотя в реальной системе момент появления следующей заявки, безусловно, неизвестен. Это необходимое допущение, принимаемое в имитационном моделировании, при длительном моделировании в статистическом смысле не влияет на адекватность модели реальной системе.Следует отметить, что планирование прихода следующей заявки необходимо провести именно в момент прихода текущей заявки, не откладывая на "потом". Если отложить планирование прихода заявки на некоторое время t0 (рис.4.1, б), а затем реализовать процедуру планирования, то фактическим интервалом прихода следующей заявки окажется величина, равная t0 + a, а не а . Случайная величина t0 + а не распределена по закону A(t) и следовательно, такое отложенное планирование нарушает закон распределения A(t) интервалов поступления заявок.Таким образом, имитационная модель в момент начала обслуживания заявки точно знает момент его окончания, хотя для реальной системы безусловно, это несправедливо.
4.2. Действия по обработке основных событийНаступление основных событий "прибытие заявки" и "окончание обслуживания" вызывают определенные, достаточно очевидные, изменения в системе и при моделировании эти изменения должны быть учтены. Приведем в начале очевидные действия, которые должны быть выполнены моделью при наступлении события "прибытие заявки".
1.Планирование прихода следующей заявки.
2.Проверка состояния обслуживающего прибора. При этом:
а) если прибор свободен, то заявка поступает на обслуживание, что вызывает переход прибора из свободного состояния в занятое; планирование события "окончание обслуживания"; б) если прибор занят, то заявка присоединяется к очереди и длина очереди увеличивается на 1.
Действия по обработке основного события "окончание обслуживания": 1. Проверка состояния очереди. При этом:
а) если в очереди нет заявок, то перевести обслуживающий прибор из занятого состояния в свободное; б) если в очереди есть заявки, то в соответствии с дисциплиной обслуживания выбирается заявка на
обслуживание, что вызывает уменьшение длины очереди, продвижения заявок в очереди и планирование события "окончание обслуживания".
4.3. Определение ближайшего событияВ выбранном нами способе коррекции таймера (способ с переменным шагом) модельное время каждый раз сдвигается на момент ближайшего события, а затем модель обрабатывает наступившее событие с учетом его типа. Возникает вопрос: как определить момент ближайшего события и его тип?Одним из способов заключается в составлении списка всех основных событий в порядке возрастания моментов времени, в которые они запланированы, и с указанием типа соответствующего события. Ясно, что ближайшее событие в таком списке окажется в начале списка и, при очередной коррекции таймера, модельное время нужно сдвинуть на момент наступления этого события, а в зависимости от его типа выполнить соответствующие действия. Такой список для рассматриваемого нами примера моделирования СМО G/G/1 в общем случае может содержать три записи следующего вида:
[Tin, "прибытие заявки" ]; |
(присутствует всегда) |
[Tout, "окончание обслуживания"]; |
(не всегда) |
[T, "завершение моделирования"]; |
(всегда). |
Здесь предполагается, что Tin Tout T.
Очевидно, что роль такого списка может быть отведена просто трем переменным Tin, Tout, T , а очередную коррекцию модельного времени выполнить согласно равенству:
tм min Tin ,Tout ,T .
Затем, в зависимости от того, какое значение приняла переменная tM , принять решение о типе события. Например, если окажется, что tм Tin , то считается, что наступило событие "прибытие заявки" и необходимо выполнить соответствующие
действия по его обработке.
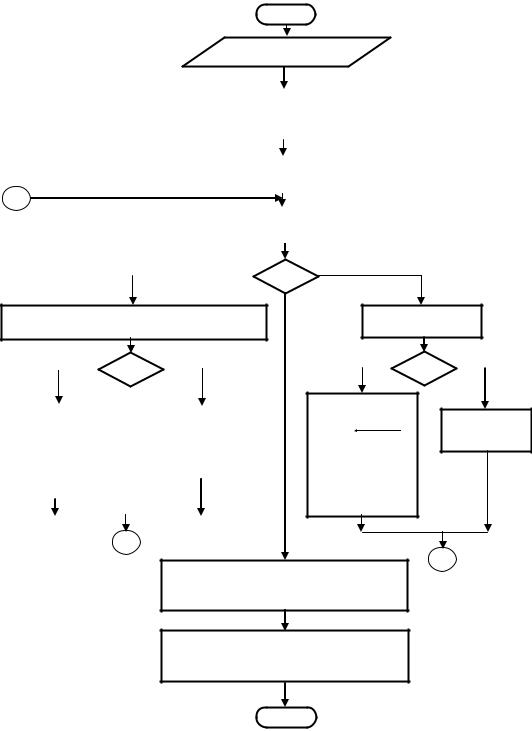
Блок 1. Ввод исходных данных, в качестве которых рассматриваются функции распределения A(t), B(t) и время моделирования Т.
Блок 2. В этом блоке обнуляются все переменные и массивы, которые предназначены для следующих целей:
F — задает состояние приборы: F = 0, если прибор свободен и F = 1, если занят.Nin — счетчик входов (определяет число вошедших в модель заявок).Nout — счетчик выходов.Nq — текущая длина очереди.Nqmax — максимальная длина очереди.Tin — момент прихода заявки.Tout— момент окончания обслуживания.Stв, St , Stu — переменные для накопления суммарных значений времен обслуживания, ожидания и пребывания соответственно.Mtq[...] — массив, который фиксирует моменты становления заявок в очередь.tм— модельное время.N0 — счетчик заявок, которые проходят очередь без ожидания.Блок 3.
Равенство |
|
|
A |
1 |
x |
означает розыгрыш случайной величины, распределенной по закону A(t), где A-1(x) — обратная |
а |
|
функция.
|
|
Начало |
|
|
|
1 Ввод исходных данных |
|
|
|
Начало |
|
|
|
A(t), B(t), T |
|
|
2 |
|
|
|
Инициализация переменных: |
|
|
|
|
|
|
|
|
F, Nin, Nout, Nq, Nqmax, Tin, Tout,Stb, St , |
|
|
3 |
|
|
|
|
|
|
|
Планирование прихода первой заявки: |
|
|
|
|
|
|
|
|
а=А-1(х); Tin=tм+ а,Tout=T+20 |
|
А |
|
|
|
4 |
|
Сдвиг модельного времени на момент |
|
|
|
|
|
|
|
ближайшего события: tм = min(Tin,Tout,T) |
|
tм =Тin |
5 |
|
tм= ? |
||
(приход |
||
|
6
Планирование прихода следующей заявки:
Nin 1, а=А-1(х); Tin=tм+ а
|
|
Y |
|
8 |
F= 0 |
N |
|
||
|
|
|
|
|
? |
|
|
Т |
|
10 |
|
|
|
|
|
11 |
= |
||
|
|
|
|
|
|
|
м |
||
|
|
|
|
|
|
|
|
t |
|
F = 1; N0 1; |
|
|
|
|
Nq 1; |
окончание( |
|||
в=В-1(х); |
|
|
|
Nqmax=max(Nq, Nqmax) |
|||||
|
|
|
|
||||||
Tout= tм+ в; |
|
|
|
|
Mtq[Nq]=tм |
|
|||
Stb=Stb+ в; |
|
|
|
|
|
|
|
||
Stu= Stu+ в |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
tм =Тout
(окончание
7 Nout 1
N 9 |
Nq= 0 |
Y |
|
|
|
|
|
12 ?
= tм- Mtq[1];
St = St + ;
Nq 1; |
Mtq[... |
] |
в=В-1(х);
Tout= tм+ в; Stb=Stb+ в; Stu= + в
13
F = 0;
Tout=T+20
А |
14 |
|
|
А |
|
|
Обработка результатов моделирования: |
|
|
|
= Stb/T; = St /(Nout+F); l = St /T;
u=Stu/(Nout+F); m = Stu/T
15
Вывод результатов моделирования:
, , l, u, m, Nqmax, Nin, Nout , F, N0, Nq , Stb, St , Stu, Mtq[...]
Конец
21 вопрос.Методы определения характеристик моделируемых систем.
При имитационном моделировании можно измерять значения любых характеристик, интересующих исследователя..
Для всей системы производится подсчёт поступивших в систему заявок, полностью обслуженных и покинувших систему заявок без обслуживания по тем или иным причинам. Соотношения этих величин характеризует производительность системы при определённой рабочей нагрузке.
По каждому потоку заявок могут вычисляться времена реакций и ожидания, количества обслуженных и потерянных заявок. По каждому устройству определяется время загрузки при обслуживании одной заявки м число обслуженным устройством заявок, время простоя устройства в результате отказов и количество отказов, возникших в процессе моделирования, дины очередей и занимаемые ёмкости памяти.
При статистическом моделировании большая часть характеристик — это случайные величины. По каждой такой характеристике yопределяется N значений, по которым строится гистограмма относительных частот, вычисляется математическое ожидание, дисперсия и моменты более высокого порядка, определяются средние по времени и максимальные значения. Коэффициенты загрузки устройств вычисляются по формуле: k=Vk*Nok/TmVk- среднее время обслуживания одной заявки к-ым устройством; Nok- количество обслуженных заявок устройством за время моделирования Tm. Определение условий удовлетворения стохастических ограничений при имитационном моделировании производится путём простого подсчёта количества измерений,
вышедших и не вышедших за допустимые пределы.

Расчёт математического ожидания и дисперсии выходной характеристики.
В случае стационарного эргодического процесса функционирования системы вычисление М(у) и Д(у) выходной характеристики у производится усреднением не по времени, а по множеству Nзнач., измеренных по одной реализации достаточной длительности. В
целях экономия ОЗУ ЭВМ М(у) и Д(у) вычисляются по рекуррентным формулам: |
mn=mn-1*(n-1)/n + y/n; |
(2) |
где mn-1 - |
математическое ожидание, вычисленное на предыдущем шаге. dn=dn-1*(n-2)/(n-1) + 1/n*(yn-mn-1)2 (3) здесь |
dn-1 - |
дисперсия, |
|
вычисленная на предыдущем шаге. При большом количестве измерений эти оценки являются состоятельными и несмещёнными.
Расчёт среднего по времени значения выходной характеристики.
Например, средняя длина очереди к каждому устройству вычисляется по формуле:
N |
|
lN li i |
Tm |
i 1 |
|
(4) где i - номер очередного изменения состояния очереди (занесение заявки в очередь или исключение
из очереди); N - количество изменений состояния очереди;
N
Ёмкость накопитель: qn qi
i 1
i
i
- интервал времени между двумя последними изменениями очереди.
Tm |
(5) |
где
q |
i |
|
- ёмкость накопителя, занятая в интервале между двумя последними обращениями к накопителю для ввода-вывода заявки.
Построение гистограммы для стационарной системы.
Г - эмпирическая плотность распределения вероятностей. Задаются границы изменения интересующей характеристики. уi [yн;ув], числом интервалов Ng. Определяется ширина интервала =( yн -ув)/Ng.
Затем в процессе моделирования по мере появления значений уi определяется число попаданий этой случайной величины в каждый из интервалов Ri гистограммы. По этим данным вычисляется относительная частота по каждому интервалу: Gi=Ri/(N* ), где N - общее число измерений у. Площадь гистограммы равна единице, равна сумме площадей:
|
N g |
|
R |
|
R |
|
Si |
Gi |
|
|
|||
i |
i |
|||||
|
|
|
|
|||
|
1 |
|
N |
|
N |
|
|
|
|
|
|
1
,
т.к.
N g N Ri 1
При необходимости выдвигается гипотеза о том, что эмпирическое распределение согласуется с некоторым теоретическим распределением. Эта гипотеза проверяется по тому или иному критерию. Например, при использовании критерия 2 в качестве меры расхождения используется выражение
|
|
N g |
|
N |
|
|
|
|
|
|
|
||
|
|
Ri |
|
Pi |
2 |
|
|
|
|
|
|||
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N Pi |
|
|
|
(6); где -
Pi
определяется из выбранного теоретического распределения
вероятность попадания случайной величины в i-ый интервал.
|
y |
i 1 |
|
|
|
|
|
|
|
|
|
||
P |
|
|
|
) F( y ) |
||
|
x dx F( y |
|||||
i |
y |
|
|
i 1 |
i |
|
|
i |
|
|
|
||
|
|
|
|
|
|
|
(7). Из теоремы Пирсона следует, что для любой функции
распределения F(y) случайной величины у при N распределения величины 2 имеет вид:
Mk (z) p( |
2 |
|
|
|
|
1 |
|
z |
k |
|
t |
|
|
z) |
|
k |
|
|
t |
1 |
|
dt |
|||||
|
|
|
|
|
2 |
|
*e |
2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
2 |
* Г( |
к |
2) 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, где z - значение случайной величины 2 ,
k=Ng-(r +1) - число степеней свободы распределения 2 .r - количество параметров теоретического распределения, Г(к/2) - гамма функция.
Функция распределения 2 табулирована. По вычисленному значению 2 и числу степеней свободы с помощью таблиц определяется вероятность Р( 2<Z). Если она превышает заданный уровень значимости С, то выдвинутая гипотеза принимается.
22 вопрос.Одноканальная модель с пуассоновским входным потоком с экспоненциальным распределением длительности обслуживания.
Простейшей одноканальной моделью с вероятностными входным потоком и процедурой обслуживания является модель, характеризуемая показательным распределением как длительностей интервалов между поступлениями требований, так и длительностей обслуживания. При этом плотность распределения длительностей интервалов между поступлениями требований имеет вид
где λ - интенсивность поступления заявок в систему Плотность распределения длительностей обслуживания:

где μ - интенсивность обслуживания Потоки заявок и обслуживании простейшие.
Пусть система работает с отказами. Необходимо определить абсолютную и относительную пропускную способность системы. Представим данную систему массового обслуживания в виде графа (рис. 4.1), у которого имеются два состояния:
S0 - канал свободен (ожидание);
S1 - канал занят (идет обслуживание заявки).
Рис. 4.1. Граф состояний одноканальной СМО с отказами
Обозначим вероятности состояний: P0(t) - вероятность состояния «канал свободен»; P1(t) - вероятность состояния «канал занят». По размеченному графу состояний (рис. 4.1) составим систему дифференциальных уравнений Колмогорова для вероятностей состояний:
Система линейных дифференциальных уравнений (4.3) имеет решение с учетом нормировочного |
условия P0(t) + P1(t) = 1. |
Решение данной системы называется неустановившимся, поскольку оно непосредственно зависит от t |
и выглядит следующим |
образом: |
|
P1(t) = 1 - P0(t) = 1 . |
(4.5) |
|
Нетрудно убедиться, |
что для одноканальной |
СМО с отказами вероятность P0(t) есть не что иное, как относительная пропускная |
способность системы q. |
|
|
Действительно, P0 - |
вероятность того, что |
в момент t канал свободен и заявка, пришедшая к моменту t, будет обслужена, а |
следовательно, для данного момента времени t среднее отношение числа обслуженных заявок к числу поступивших также равно P0(t), т. е.
q = P0(t), |
(4.6) |
|
По истечении большого интервала времени (при |
) достигается стационарный (установившийся) режим: |
|
Зная относительную пропускную способность, легко найти абсолютную. Абсолютная пропускная способность (А) - среднее число заявок, которое может обслужить система массового обслуживания в единицу времени:
Вероятность отказа в обслуживании заявки будет равна вероятности состояния «канал занят»:
Данная величина Pотк может быть интерпретирована как средняя доля необслуженных заявок среди поданных.
23 вопрос.Одноканальная система массового обслуживания с ожиданием.
Моделирование СМО pdf 4.2.2 стр 8
Система массового обслуживания имеет один канал. Входящий поток заявок наобслуживание - простейший поток с интенсивностью . Интенсивность потокаобслуживания равна (т. е. в среднем непрерывно занятый канал будет выдавать обслуженных заявок). Длительность
обслуживания - случайная величина, подчиненнаяпоказательному закону распределения. Поток обслуживании является простейшимпуассоновским потоком событий. Заявка, поступившая в момент, когда канал занят,становится в очередь и ожидает обслуживания.Предположим, что независимо от того, сколько требований поступает на входобслуживающей системы, данная система (очередь + обслуживаемые клиенты) не можетвместить более N-требований (заявок), т. е. клиенты, не попавшие в ожидание,вынуждены обслуживаться в другом месте. Наконец, источник, порождающий заявки

наобслуживание, имеет неограниченную (бесконечно большую) емкость.Граф состояний СМО в этом случае имеет вид, показанный на рис. 4.2.Состояния СМО имеют следующую интерпретацию:
S0 - «канал свободен»;
S1 - «канал занят» (очереди нет);
S2 - «канал занят» (одна заявка стоит в очереди); Sn- «канал занят» (n -1 заявок стоит в очереди);
SN - «канал занят» (N - 1 заявок стоит в очереди). Стационарный процесс в данной системе будет описываться следующей системой алгебраических уравнений:
где .
Решение приведенной выше системы уравнений (4.10) для нашей модели СМО имеет вид
Следует отметить, что выполнение условия стационарности для даннойСМО не обязательно, поскольку число допускаемых в обслуживающую систему заявокконтролируется путем введения ограничения на длину очереди (которая не
может превышать N - 1), а не соотношением между интенсивностями входного потока, т. е. неотношением  Определим характеристики одноканальной СМО с ожиданием и ограниченнойдлиной очереди, равной (N - 1):
Определим характеристики одноканальной СМО с ожиданием и ограниченнойдлиной очереди, равной (N - 1):
вероятность отказа в обслуживании заявки; относительная пропускная способность системы; абсолютная пропускная способность соответственно
среднее число находящихся в системе заявок; среднее время пребывания заявки в системе; средняя продолжительность пребывания клиента (заявки) в очереди; среднее число заявок (клиентов) в очереди (длина очереди); соответственно
24 вопрос.Многоканальная модель с пуассоновским входным потоком и экспоненциальным распределением длительности обслуживания.
В подавляющем большинстве случаев на практике системы массового обслуживания являются многоканальными, и, следовательно, модели с n обслуживающими каналами (где n > 1) представляют несомненный интерес.
Процесс массового обслуживания, описываемый данной моделью, характеризуется интенсивностью входного потока λ , при этом
параллельно может обслуживаться не более n клиентов (заявок). Средняя продолжительность обслуживания одной |
заявки |
равняется 1/μ . Входной и выходной потоки являются пуассоновскими. Режим функционирования того или |
иного |
обслуживающего канала не влияет на режим функционирования других обслуживающих каналов системы, причем длительность процедуры обслуживания каждым из каналов является случайной величиной, подчиненной экспоненциальному закону
распределения. |
Конечная цель использования n параллельно включенных обслуживающих каналов заключается в |
повышении |
(по сравнению |
с одноканальной системой) скорости обслуживания требований за счет обслуживания одновременно |
n клиентов. |
Граф состояний многоканальной системы массового обслуживания с отказами имеет вид, показанный на рис. 4.3. |
|
|
Рис. 4.3. Граф состояний многоканальной СМО с отказами
Состояния СМО имеют следующую интерпретацию: S0 - все каналы свободны;
S1 - занят один канал, остальные свободны;
…………………………………………………….
Sk - заняты ровно k каналов, остальные свободны;
