
- •Содержание
- •1. Общие вопросы моделирования
- •1.1. Предмет теории моделирования
- •1.2. Классификация моделей
- •1.3. Классификация объектов моделирования
- •1.4. Основные этапы моделирования
- •2. Технология моделирования
- •2.1. Создание концептуальной модели
- •2.2. Подготовка исходных данных
- •2.3. Разработка математической модели
- •3. Математические схемы моделирования систем.
- •3.1. Основные подходы к построению математических моделей систем
- •3.2. Непрерывно-детерминированные модели (д-схемы)
- •3.3. Дискретно-детерминированные модели (f-схемы)
- •4. Непрерывно-стохастические модели (q-схемы)
- •4.1. Понятие случайного процесса
- •4.1.1. Марковский случайный процесс
- •4.1.2. Потоки событий
- •4.1.3. Уравнения Колмогорова для вероятностей состояний. Финальные вероятности состояний
- •4.2. Задачи теории массового обслуживания
- •4.3. Классификация систем массового обслуживания
- •4.4. Математические модели простейших систем массового обслуживания
- •4.4.1. Одноканальная смо с отказами
- •4.4.2. Одноканальная смо с ожиданием
- •4.4.3. Одноканальная смо с ожиданием без ограничения на длину очереди
- •4.4.4.МногоканальнаяСмо с отказами(задача Эрланга)
- •4.4.5.Многоканальная смо с ожиданием
- •4.4.6. Модель обслуживания машинного парка
- •5. Сетевые модели (n-схемы). Сети Петри
- •5.1. Теоретические основы сетей Петри: принципы построения, алгоритмы поведения
- •5.1.1. Введение в теорию комплектов
- •5.1.2. Структура сети Петри
- •5.1.3. Графы сетей Петри
- •5.1.4. Маркировка сетей Петри
- •5.1.5. Правила выполнения сетей Петри
- •5.2. Сети Петри для моделирования систем: способы реализации
- •5.2.1. События и условия
- •5.2.2. Одновременность и конфликт
- •6. Обощенные модели (a-схемы)
- •6.1. Структура агрегативной системы
- •6.2. Кусочно-линейные агрегаты
- •7. Имитационное моделирование систем
- •7.1. Процедура имитационного моделирования
- •7.2. Обобщённые алгоритмы имитационного моделирования
- •7.2.1. Алгоритм моделирования по принципу особых состояний
- •7.2.2. Алгоритм моделирования по принципуt
- •7.3. Этапы имитационного моделирования
- •8. Статистическое моделирование приборных систем
- •8.1. Теоретические основы метода статистического моделирования
- •8.2. Моделирование случайных величин
- •8.2.1. Табличный способ
- •8.2.2. Аппаратный способ
- •8.2.3. Алгоритмический способ
- •8.3. Моделирование случайных событий с заданным законом распределения
- •8.3.1. Разыгрывание дискретной случайной величины
- •8.3.2. Разыгрывание непрерывной случайной величины
- •8.2.3. Разыгрывание случайной величины, распределенной нормально
- •8.4. Моделирование систем массового обслуживания с использованием метода Монте-Карло
4.4.4.МногоканальнаяСмо с отказами(задача Эрланга)
Дано: в системе имеетсяnканалов, на которые поступает поток заявок с интенсивностью. Поток обслуживаний имеет интенсивность. Заявка, заставшая систему занятой, сразу же покидает ее.
Найти: абсолютную и относительную пропускную способность СМО; вероятность того, что заявка, пришедшая в момент времениt, получит отказ; среднее число заявок, обслуживаемых одновременно (или, другими словам, среднее число занятых каналов).
Решение. Состояние системыS(СМО) нумеруется по максимальному числу заявок, находящихся в системе (оно совпадает с числом занятых каналов):
S0– в СМО нет ни одной заявки;
S1– в СМО находится одна заявка (один канал занят, остальные свободны);
S2– в СМО находится две заявки (два канала заняты, остальные свободны);
. . .
Sn– в СМО находитсяnзаявок (всеnканалов заняты).
Граф состояний СМО представлен на рис. 4.7

Рис. 4.7. Граф состояний для n-канальной СМО с отказами
Из состояния S0в состояниеS1систему переводит поток заявок с интенсивностью(как только приходит заявка, система переходит изS0вS1). Если система находилась в состоянииS1и пришла еще одна заявка, то она переходит в состояниеS2и т.д.
Пусть система находится в состоянии S1(работает один канал). Он производитобслуживаний в единицу времени. Поэтому дуга перехода из состоянияS1в состояниеS0нагружена интенсивностью. Пусть теперь система находится в состоянииS2(работают два канала). Чтобы ей перейти вS1, нужно, чтобы закончил обслуживание первый канал, либо второй. Суммарная интенсивность их потоков равна 2и т.д.
Выходные характеристики (характеристики эффективности) данной СМО определяются следующим образом.
Абсолютнаяпропускнаяспособность:

где n– количество каналов СМО;p0– вероятность нахождения СМО в начальном состоянии, когда все каналы свободны (финальная вероятность нахождения СМО в состоянииS0).
Для того чтобы написать формулу для определения p0, рассмотрим рис. 4.8.

Рис. 4.8. Граф состояний для схемы «гибели и размножения»
Граф, представленный на этом рисунке, называют графом состояний для схемы «гибели и размножения».

Остальные финальные вероятности состояний СМО запишутся следующим образом.
Вероятность того, что СМО находится в состоянии S1, когда один канал занят:
![]()
Вероятность того, что СМО находится в состоянии S2, т.е. когда два канала заняты:
![]()
Вероятность того, что СМО находится в состоянии Sn, т.е. когда все каналы заняты.
![]()
Теперь для n-канальной СМО с отказами

При этом
![]()
![]()
![]()
Относительная пропускная способность(средняя доля заявок, обслуживаемых системой):
![]() .
.
Вероятностьотказа(вероятность того, что заявка покинет СМО необслуженной):
![]() .
.
Среднее число занятых каналов(среднее число заявок, обслуживаемых одновременно):
![]() .
.
4.4.5.Многоканальная смо с ожиданием
Пусть многоканальная система массового обслуживания с ожиданием имеет Sканалов обслуживания. Входной и выходной потоки являются пуассоновскими с интенсивностямиисоответственно. Средняя продолжительность обслуживания одного клиента равна – 1/.
В установившемся режиме функционирование многоканальной СМО с ожиданием и неограниченной очередью может быть описано с помощью системы алгебраических уравнений:
 .
.
Решение данной системы уравнений имеет вид:
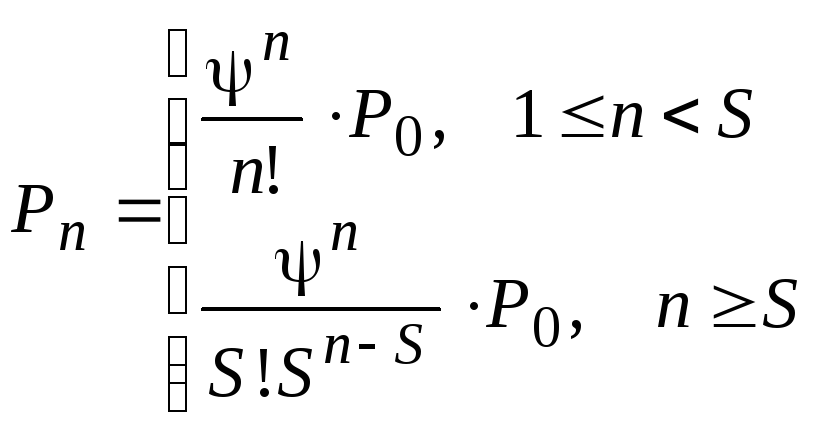 ,
,
где =/; .
.
Решение будет действительным, если
выполняется условие
![]() .
.
Вероятностные характеристики функционирования в стационарном режиме многоканальной СМО с ожиданием и неограниченной очередью определяются по следующим формулам:
вероятность того, что в системе находится n клиентов на обслуживании:
 ;
;
среднее число клиентов в очереди на обслуживание:
![]() ;
;
среднее число находящихся в системе клиентов(заявок на обслуживание и в очереди):
![]() ;
;
средняя продолжительность пребывания клиента (заявки на обслуживание) в очереди:
![]() ;
;
средняя продолжительность пребывания клиента (заявки на обслуживание) в системе:
![]() .
.
