Лабы / 5 / otchet_nash3

МИНОБРНАУКИ РОССИИ

Федеральное государственное автономное образовательное учреждение

высшего образования

“Санкт-Петербургский государственный электротехнический университет «ЛЭТИ»

им. В.И. Ульянова (Ленина)” (СПбГЭТУ «ЛЭТИ»)

Кафедра ИИСТ

Лабораторная работа №1

«Моделирование измерительного канала (термопара)»

Выполнили:

Студенты группы

Проверил:

Санкт-Петербург 201 г.

Задание 5

1. Ознакомиться с характеристиками преобразователя (термопара типа S), Т от -50 до 1064.

2. Создать модель термопары типа ТПП с характеристикой преобразования

A₀=0; A₁=5,39957823*10^-3; A₂=1,25197700*10^-5; A₃=-2,24482180*10^-8; A₄=2,84521649*10^-11; A₅=-2,24405845*10^-14; A₆=8,50541669*10^-18;

по аналогии с П.1. Т от 0 до 1600.

3. Ввести неидеальность в модели обоих каналов

1. 0 ÷ 300 0,008

2. 300 ÷ 1600 ΔE_t = 0,008 + 2,69*10^-5(t - 300)

Структурная схема канала:

где ТП – первичный измерительный преобразователь (термопара), НП – нормирующий преобразователь, АЦП – аналогово-цифровой преобразователь, МП – масштабирующий преобразователь, ОП – обратное преобразование, И – индикатор (вывод результата).

Реализация и расчет всех измерительных блоков выполнены в программной среде LabVIEW 11

1. Ознакомление с характеристиками преобразователя

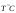
Лицевая панель виртуального инструмента выглядит следующим образом:

Рисунок 1. - Лицевая панель виртуального инструмента.

На лицевой панели представлены:

1. Пути к файлам (идет запись табличных значений в блокнотовский файл), и путь к блокнотовскому файлу, из которого идет считывание образцовых данных. ВИ: file path

2. Графики температур измеренной и образцовой. ВИ: XY Graph

3. График разности образцовой и измеренной температур. ВИ: Waveform Graph

4. Два массива, содержащие данные измеренной и образцовой температур. В левом столбце массивов – значение температуры, в правом – напряжение (значения ЭДС термопары в соответствии с температурой).

5. Таблица со значениями, полученными вычитанием массива данных измеренной температуры из массива данных с образцовыми измерениями.

Блок диаграмма выглядит следующим образом:

Рисунок 2. - Блок диаграмма

Данный фрагмент программы является моделью первичного измерительного преобразователя. Вся программа находится в структуре Flat Sequence Structure (открытая последовательность). Значения, которые выдает термопара вычисляются с помощью заданных формул в узле Formula Node. Для того, чтобы не вводить каждый раз какую-то определенную температуру, зациклили измерение с помощью цикла While Loop. Таким образом происходит измерение температур в интервале от 0 до 1600 с шагом в 10 градусов.

Значения массива VI_measured – значения температуры и напряжения, полученные с помощью виртуального инструмента в LabView, при использовании условий из задания; значения массива obrazec – значения температуры и напряжения для термопар типа ТПП (платинородий-платиновая) (тип S), полученные с помощью стандартного инструмента Convert Thermocouple Reading (эти значения полностью совпадают со значениями из справочника). Чтобы показать точность измерений, вычитаем из массива obrazec массив VI_measured. Получившиеся значения разности представлены в таблице Raznost’.

Вывод: Эксперементально расчитанная характеристика практически совпадает со значениями, полученными из справочника, что позволяет использовать данный виртуальный инструмент. Погрешность измерений не превышает 6 мкВ, что видно на графике и таблице погрешностей.

2. Создание измерительного канала

Рисунок 3. – Структура измерительного канала.

В первом пункте данной работы был собран первичный измерительный преобразователь, который выдавал значения температуры и напряжения, причем с приемлемой погрешностью. Тогда мы можем начинать сборку измерительного канала сразу же с НП (Нормирующий Преобразователь). Он необходим для корректной работы АЦП. Диапазон изменения сигнала полученного от ПИП необходимо привести к диапазону АЦП.

Блок диаграмма выглядит следующим образом:

Рисунок 4. - Блок диаграмма

Коэффициент k, преобразующий диапазон изменения входного напряжения, можно рассчитать по формуле: , (1)

где и соответственно максимальное и минимальное напряжения, которые можно подавать на АЦП, , .

Примем , , тогда

Для дальнейшего преобразования используем АЦП, с n = 10. Максимальное число уровней . , (2)

Лицевая панель виртуального инструмента:

Рисунок 5. - Лицевая панель виртуального инструмента

Масштабирующий преобразователь (МП) служит для приведения полученного кода к диапазону и единицам измерения физической величины (температуры).

Рисунок 6. - Лицевая панель виртуального инструмента

Получили значения температуры на выходе измерительного канала. Сравним эти значения с исходными. На рисунке 7 видно, что разница при температуре, например, 700°С превышает 100 градусов.

Рисунок 7. - Лицевая панель виртуального инструмента

Вводим обратное преобразование (ОП), компенсирующее нелинейность (ПКН) всех предыдущих преобразований (рисунки 8-10).

Рисунок 8. - Лицевая панель виртуального инструмента

Рисунок 9. - Лицевая панель виртуального инструмента

Рисунок 10. - Блок диаграмма

В результате значения на выходе функции масштабирующего преобразования ИП является также значениями обратной функции преобразования, поскольку значения исходной зависимости были последовательно проведены через все последующие преобразователи.

Необходимо провести аппроксимацию получившейся функции с целью получения аналитического выражения для неё. Было принято решение провести кусочную полиномиальную аппроксимацию вида:

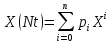
Диапазон измерений был разбит на четыре равномерных участка.

В цикле For Loop разбили диапазон (160 измерений) на четыре одинаковые части (по 40 измерений каждая). Для каждой строки массива будет проведена аппроксимация и найдены коэффициенты аппроксимации с помощью функции General Polynomial Fit, расчет которых происходит методом наименьших квадратов.

Вид графика погрешности (рисунок 9) обусловлен тем, что аппроксимация проводилась методом наименьших квадратов, суть которого заключается в нахождении минимальной суммы квадратов отклонения: .

Рисунок 11. - Таблица результатов с шагом 100°С

Приведена таблица результатов – промежуточные значения всего измерительного канала для 16 точек из 160 возможных. Эта же таблица сохраняется в файл (рисунок 11).

Рисунок 12. – Сохранение результатов в файл

3. Введение неидельности в модель.

Рисунок 13. - Таблица результатов с шагом 100°С после введения неидеальности в модель

Разница между нормальными значениями и значениями с введенной неидеальностью менее 1% для любого из промежуточных этапов программы и для любой измеряемой температуры.

Рисунок 14. - Блок диаграмма

Выводы: В результате работы была получена модель измерительного канала. Данная модель имитирует работу термопары типа S, и делает необходимые преобразования полученного сигнала для его измерения. Была рассчитана аппроксимация аналитического выражения функции обратного преобразования (рисунок 8) и представлена её погрешность (рисунок 9).

Разница между нормальными значениями (рисунок 11) и значениями с введенной неидеальностью (рисунок 13) менее 1% для любого из промежуточных этапов программы и для любой измеряемой температуры.