ФИЗИЧЕСКИЕ ОСНОВЫ АКУСТИЧЕСКОГО КОНТРОЛЯ

звука в воде. Обозначим через значение коэффициента прохождения при нормальном падении Максимум на рис 8а п р и н а з о в е м первым, а около - вторым. Наличие острых максимумов и минимумов на угловой зависимости обусловлено выполнением условий четвертьволновой и полуволновой пластин. Примем за значения коэффициента прохождения в первом максимуме а значение угла падения, при котором он достигается за . Для второго максимума примем обозначения соответственно. Зависимости Т(0), от коэффициента неоднородности к представлены на рис.9 Видно, что в слабо неоднородном (к<1) и сильно неоднородном 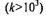пределах влияние степени неоднородности незначительно. Наиболее существенные изменения происходят в интервале 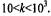Для понимания этих зависимостей следует рассмотреть подробнее распределение модулей в пластине. Согласно (41), изменение модуля на толщине пластины равно

В пределе сильной неоднородности изменение модулей близко к В противоположном случае это и з м е н е н и е Ф и з и ч е с к а я картина распространения волн принципиально различна в этих двух случаях. При влияние неоднородности невелико, во всяком случае для углов падения, меньших первого кришческого. Коэффициент прохождения близок к значениям для однородной ТИ пластины, а влияние неоднородности должно сказываться на ходе лучей через явление рефракции. В противоположном случае толщина слоя, где происходит большая часть изменения модулей, значительно меньше длины волны ультразвука. В этом случае прохождение через пластину с непрерывно меняющимися модулями подобно прохождению через пластину, составленную из двух однородных слоев с различными значениями модулей.

32

Влияние неоднородности плотности пластины

Неоднородность плотности, в принципе, возможна в переходной области 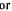изотропного металла свариваемой детали к наплавленному трансверсально - изотропному аустениту сварного шва. Зависимость коэффициента прохождения сквозь неоднородную пластину от угла падения показана на рис.10. Закон изменения плотности подобен показанному в (41), причем роль максимального

изменения играет отношение минимальной 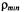к максимальной плотностей: Коэффициент неоднородности к на рис.10 равен 100. Толщина пластины

Рис.10. Влияние неоднородности плотности ТИ среды на угловую зависимость коэффициента прохождения

Близкая к однородной по плотности пластина с 5=0,99 имеет зависимость с максимумом около соответствующим условию полуволновой пластины для волны QL и двумя острыми максимумами вблизи отвечающим условию четвертьволновой пластины для волн типа QSV. Но мере увеличения неоднородности плотности оба максимума смещаются в область меньших углов падения. Максимум, соответствующий QL волне, смещается при этом в область больших углов и поглощает один из острых максимумов.

Влияние толщины пластины

Вид интерференционной картины волн в пластине, очевидно, радикальным образом зависит от ее толщины, см. рис.11. В зависимости от толщины пластины наблюдается серия максимумов коэффициента прохождения. Интерференционная картина волн в пластине, в том числе выполнение условий четверть- и полуволновых пластин, определяется набегом

фазы- волновое число, зависящее от координаты z. В

однородной пластине увеличение частоты волны эквивалентно пропорциональному уменьшению толщины пластины.

34

Влияние абсолютной величины изменения модулей Как отмечалось выше, распределение модулей по пластины

сильно отличается в зависимости от значений коэффициента неоднородности к. Поэтому и влияние абсолютной величины изменения модулей различно при разных к. На рис.14 показаны угловые зависимости коэффициента прохождения Т для трех значений соответствующих практически однородной, умеренно неоднородной и сильно неоднородной пластинам. Параметр показывает абсолютную величину изменения. Кривые на рис.14 относятся к изотропной, однородной ТИ пластине и пластинам с разными значениями Толщина пластины на рис.14 составляет 0,27 см. Детальная структура максимумов и минимумов зависит как от параметра так и от к. Особенно следует отметить область ненулевых значений коэффициента передачи при В этой области углов падения, превышающих первый критический угол в пластине после преломления на границе возбуждаются только волны типа QSV; максимум при на рис. 14а обусловлен резонансными условиями именно для этих волн. При увеличении к этот максимум исчезает, см. рис.14б,в.

36

Прохождение через ТИ пластину: отличие от изотропной пластины

Согласно расчетам, результаты которых представлены на рис.14, радикальное отличие изотропной от ТИ пластины аустенита зафиксировано в области углов, значительно превышающих первый критический. В ТИ пластине существует область значений углов падения 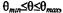где коэффициент прохождения однородных волн отличен от нуля.

Наличие этого интервала объясняется сложной формой поверхностей рефракции аустенита. В качестве примера на рис. 15 показано сечение поверхностей рефракции и схема образования двух отраженных волн типа QSV и одной волны SH при падении одной SH волны на границу ТИ среды. Физическую картину явлений преломления волн и трансформации из продольной в жидкости в волны QL и QSV в аустенитной стали можно пояснить следующим образом. Существо состоит в немонотонной зависимости скорости QSV волны от угла между осью ТИ среды и направлением волнового вектора. Убедиться в немонотонности можно и на основе анализа формул для фазовой скорости собственных волн. Вследствие этого зависимость величины определяющая угол преломления волны QSV, также немонотонна. Максимум этой зависимости приходится на угол соответствует углу преломления, равному

области углов одному углу падения соответствует два решения уравнения закона Снеллиуса, два значения угла преломления и две QSV волны. Для каждой из этих волн устанавливается своя интерференционная картина в пластине. По мере увеличения угла падения угол преломления одной из этих QSV волн как и обычно увеличивается, а второй аномально уменьшается. В точке эти две волны сливаются в одну, а при решение в виде однородных плоских волн отсутствует.

Рис. 15. Поверхности рефракции аустенита и образование двух волн типа QSV

Проведенный анализ показывает, что достигнут реальный прогресс в моделировании упругих свойств аустенитной стали сварного шва. Доказана

37

приемлемость модельной ТИ среды для этой цели. Разработаны алгоритмы и составлены программы расчетов упругих полей, с учетом упругой анизотропии и неоднородности среды. Определенные перспективы и значительное упрощение расчетов обещает использование аналитических формул для фазовых и групповых скоростей волн. Трассировка лучей, использующая решение уравнения закона отражения и преломления в элементарных объемах среды и простые аналитические выражения для скоростей, могла бы в ближайшее время обеспечить построение практической методики УЗ контроля. Неоднородность упругих модулей и плотности ТИ среды относительно просто учесть для сильно неоднородной среды. В этом случае среда может быть условно разделена на два участка, в пределах каждого параметры среды можно считать постоянными.

Таким образом, в пятой главе приведены методы решения уравнений теории упругости в неоднородной среде. Рассмотрены, в основном, слоистые среды, параметры которых изменяются вдоль одной координаты. Изложены методы решения уравнений как для сред с непрерывным изменением параметров, так и для дискретно-слоистых сред. Основным практически важным результатом главы можно считать детальное рассмотрение упругих волн в пластине аустенитной стали в модели трансверсально-изотропной среды. Рассчитан коэффициент прохождения волн через пластину и показано, что существуют радикальные отличия для случаев изотропной и трансверсально-изотропной пластины. Отличие выражается в дополнительном интервале прозрачности ТИ пластины в области углов падения, которая для изотропной пластины относится к интервалу углов, больших второго критического. Учтено влияние неоднородности модулей упругости на коэффициент прохождения.

ОСНОВНЫЕ ВЫВОДЫ И РЕЗУЛЬТАТЫ ДИССЕРТАЦИОННОЙ РАБОТЫ Представляются важными следующие выводы, которые можно сделать на

основе проведенной работы.

1.Модель трансверсально-изотропной среды способна адекватно описать характеристики упругих волн в материале сварного шва из аустенитной и аустенитно-ферритной стали.

2.Магнитная поляризация оказывает заметное влияние на распространение ультразвука, если в материале присутствует ферроили ферримагнитная фаза. Влияние магнитной поляризации может проявляться в изменениях поляризации собственных волн, в интерференции мод, следовательно, в явлениях вращения плоскости поляризации и эллиптичности.

3.Магнитная поляризация приводит к некоторому отклонению вектора лучевой скорости и потока энергии. Это отклонение особенно существенно в условиях эффекта внутренней конической рефракции.

4.Для выявления эффектов, вызванных гиротропией и магнитной поляризацией, следует выбирать направление распространения и поляризацию

38

волны, а также направление магнитного поля таким образом, чтобы ожидаемое явление без магнитной поляризации отсутствовало.

5.Получен тензор модулей упругости намагниченной трансверсальноизотропной среды и решена задача Кристоффеля для упругих волн в такой среде.

6.Показано, что явления вращения плоскости поляризации и эллиптичности поперечных волн в ферромагнитном металле в квазистатической области частот могут быть использованы в неразрушающем УЗ контроле структуры и фазового состава.

7.Экспериментально и теоретически доказано существование аномалий в структуре акустических полей поперечных волн в монокристаллах

вусловиях эффекта внутренней конической рефракции.

8.На основе детального изучения прохождения упругих волн через пластину неоднородного материала, моделируемого трансверсальноизотропной средой показано, что действие анизотропии приводит к появлению дополнительной области акустической прозрачности.

9.Развита методика определения времени релаксации электронов в монокристаллах высокочистых металлов с использованием магнитоакустических явлений.

Основные положения диссертации опубликованы в следующих работах

1.Волкова Н.Н., Ринкевич А.Б., Смородинский Я.Г., Фридман Г.Г. Упругие волны в намагниченной трансверсально - изотропной среде // Дефектоскопия. 1993. N4. С.3-10.

2.Rinkevich A.B., Smorodinsky Ya.G. Simple model calculation of elastic wave propagation in the austenitic steel // Nondestructive Testing and Evaluation. 1988. V.14.P.393-402.

3.Ринкевич А.Б., Смородинский Я.Г., Волкова Н.Н., Загребин Б.Н. Групповая скорость ультразвука в трансверсально - изотропной среде // Дефектоскопия. 1994. N2. С.58-63.

4.Смородинский Я.Г. Лучевая скорость в аустените в модели трансверсальноизотропной среды // Дефектоскопия. 1999. N 4, С.3-8.

5.Rinkevich A., Smorodinsky Ya., Vlasov K.B., Kroning M, Spies M. The Internal Conical Refraction of Ultrasound in Cubic Crystals, Fraunhofer Institut Zerstorungfreie Prafverfahren. Saarbriicken, 1999. P.56.

6.Ринкевич А.Б., Смородинский Я.Г., Власов К.Б., Кренинг М, Шпис М. Внутренняя коническая рефракция ультразвука в кубических кристаллах, Екатеринбург: Изд. УрО РАН, 2000.72с.

7.Ринкевич А.Б.,Смородинский Я.Г. Физические основы акустического контроля, Екатеринбург, Изд. "Таймер", 2001.112с.

8.Смородинский Я.Г. Упругие волны и магнитоакустические явления в намагниченной трансверсально-изотропной среде, Екатеринбург, Изд. УрО РАН,2004г.112 с,

39

9.Бебенин Н.Г., Смородинский Я.Г. Поглощение звука в диэлектриках со спиральной магнитной структурой // Физика твердого тела. 1986. Т. 28. № 4.

С.1115-1118.

10.Власов К.Б., Розенберг Е.А., Тимощук В.И., Смородинский Я.Г. Наблюдение температурного гистерезиса намагниченности монокристалла гематита вблизи перехода Морина. // Физика твердого тела. Т.28. № 11. 1986. С.3287-3292.

11 .Власов К.Б., Ринкевич А., Смородинский Я.Г., Гвентер А.Е. Дисперсионные соотношения при магнитоакустических явлениях в металлах // Физика металлов и металловедение. 1989. Т. 67. № 3. С.471-482.

12.Ринкевич А.Б., Смородинский Я.Г., Насыров Р.Ш. Измерение характеристик рассеяния электронов проводимости в металлах с помощью ультразвука // Высокочистые вещества. 1989. Т. 2. № 3. С.42-45.

13.Кобелев А.В., Смородинский Я.Г. Эффекты связи мод в угловой зависимости полей ФМР в двуслойной магнитосвязанной пленке с перпендикулярной анизотропией // Физика твердого тела. 1989. Т. 31. № 10. С.6-12.

14.Ринкевич А.Б., Смородинский Я.Г. Дисперсия скорости ультразвука при допплер-сдвинутом акустическом циклотронном резонансе в молибдене // Физика металлов и металловедение. 1990. Т.69. № 3. С.48-54.

15.Ринкевич А.Б., Смородинский Я.Г. Точность измерения характеристик электронов проводимости в металлах с помощью ультразвука // Высокочистые вещества. 1990. Т. 3. № 6. С.192-196.

16.Ринкевич А.Б., Смородинский Я.Г., Физические основы неразрушающего контроля изделий из чистых металлов // Дефектоскопия. 1994. № 1. С.79-84.

17.Rinkevich A., Smorodinsky Ya. Electron Absorption of Ultrasound in Plastically Deformed Tungsten // J. Phys.: Condensed Matter. 1994. V.6. № 3. P. 693-698.

18.Ринкевич А.Б., Смородинский Я.Г. Методы расчета в магнитной ультразвуковой структуроскопии // Дефектоскопия. 1995. № 9. С.33-36.

19.Смородинский Я.Г. Моделирование свойств реакторных материалов // Дефектоскопия. 1995. № 9. С.6-7

20.Смородинский Я.Г. Расчет поляризации упругих волн в трансверсальноизотропном аустените /(Дефектоскопия. 1999. № 4. С.9-12.

21.Ринкевич А.Б., Смородинский Я.Г., Щербинин В.Е., Хюбшен Г., Шпис М. Магнитоакустические эффекты в никеле в квазистатической области частот. //ФММ.2000.Т.89.№2.С.59-64.

22.Ринкевич А.Б., Смородинский Я.Г., Бурханов A.M., Кривоносова А.С., Келер Б. Анализ ультразвуковых полей и выявление дефектов в монокристаллах алюминия методом лазерного детектирования // Дефектоскопия. 2000. №11. С.64-74

23.Ринкевич А.Б., Смородинский Я.Г. Упругие волны в неоднородной пластине аустенита в модели трансверсально-изотропной среды // Дефектоскопия. 2001.№7.С.40-64.

40

24.Ринкевич А.Б., Перов Д.В., Смородинский Я.Г., Келер Б. Применение вейвлетов для анализа ультразвуковых полей, детектированных лазерным интерферометром. Обнаружение и локализация дефекта в монокристалле алюминия //Дефектоскопия. 2001. № 12. С.67-80.

25.Кривоносова А.С., Ринкевич А.Б., Смородинский Я.Г. Акустические поля в монокристаллах алюминия, детектированные лазерным интерферометром. — Акустический журнал, 2001, т.47, №1, С.76-84.

26.Ринкевич А.Б., Смородинский Я.Г. Анализ параметров и технических характеристик современных ультразвуковых дефектоскопов общего назначения //Дефектоскопия. 2002. № 9. С.3-27.

27.Перов Д.В., Ринкевич А.Б., Смородинский Я.Г. Вейвлетная фильтрация сигналов ультразвукового дефектоскопа. //Дефектоскопия. 2002. №12. С. 3-20.

28.Rinkevich A., Smorodinsky Ya. Ultrasonic Energy Distribution in Aluminum Single Crystals //Nondestructive Testing and Evaluation. 2002. V. №. P. 159-170.

29.Ринкевич А.Б., Смородинский Я.Г. Отражение, преломление и распространение упругих волн в магнитно-поляризованном аустените сварного шва//Депонировано ВИНИТИ №1088-В-92. М. 1992.

ЗО.Ринкевич А.Б., Смородинский Я.Г., Борисов А.Б., Зверев В.В. Изучение распространения упругого поля в слоисто-неоднородных средах и установление взаимосвязи изменения параметров поля и степени неоднородности среды // Отчет о НИР ИФМ УрО РАН, г.Екатеринбург, 1991, хУд 51/92.

31.Ринкевич А.Б., Смородинский Я.Г. Распространение упругого поля и поток энергии в трансверсально-изотропном аустените // Отчет о НИР ИФМ УрО РАН, г.Екатеринбург, 1993.

32.Власов К.Б., Ринкевич А.Б., Смородинский Я.Г. Магнитоакустический резонанс в вольфраме и молибдене // Материалы XII Всесоюзной конф. по акустоэлектронике и квантовой акустике, Саратов, 1983.

33.Власов К.Б., Ринкевич А.Б., Смородинский Я.Г. Измерение времени релаксации электронов по эллиптичности ультразвука // Материалы XIV Всесоюзной конф. по акустоэлектронике и квантовой акустике, Кишинев, 1989.

34.Ринкевич А.Б., Смородинский Я.Г. Поглощение и скорость ультразвука в деформированном вольфраме // Материалы XI Всесоюзной акустической конференции, Москва, 1991.

35.Смородинский Я.Г., Ринкевич А.Б., Волкова Н.Н. Влияние намагниченности на параметры распространения ультразвука в сварном шве // Материалы XIV научно-технической конференции по ультразвуковому контролю, С.-Петербург, 1992, С.50.

36.Смородинский Я.Г., Ринкевич А.Б. Угловая зависимость групповой скорости ультразвука в аустенитном сварном шве // XIII научно-техническая конференция "Неразрушающие физические методы и средства контроля", С.-Петербург, 1993, С. 16.