ФИЗИЧЕСКИЕ ОСНОВЫ АКУСТИЧЕСКОГО КОНТРОЛЯ

21

волн перпендикулярно внешнему магнитному полю, представляют собой акустический аналог эффекта Коттона-Мутона с учетом магнитного дихроизма.

Исходя из результатов измерений, в исследованных условиях угол поворота 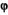невелик. Это значит, что сравнительно мало влияние магнитного дихроизма. Действительно, в металле наиболее существенную часть потерь в квазистатической области дают потери на вихревые токи. Этот вклад присутствует у собственных волн обеих поляризаций. В наших экспериментах

поляризационные явления. Они возникают за счет добавок к действительным и мнимым компонентам волнового вектора и присутствуют в условиях эффекта внутренней конической рефракции упругих волн. В кристалле никеля в рассматриваемых условиях преобладающим оказалось магнитоакустическое двулучепреломление, приводящее к заметной эллиптичности поперечного ультразвука.

В монокристаллах металлов особой чистоты при низких температурах может существовать явление доплер-сдвинутого акустического циклотронного резонанса (ДСАЦР), которое состоит резонансном взаимодействии групп электронов проводимости с ультразвуковой волной и проявляется . в существовании резких пиков поглощения поперечного ультразвука в магнитном поле. Явление ДСАЦР помимо резонанса в поглощении сопровождается еще и появлением эллиптичности поперечного ультразвука. При этом поляризация ультразвука из линейной становится эллиптической после прохождения волны через образец. Теоретически и экспериментально установлено, что зависимость отношения полуосей эллипса Б ОТ напряженности магнитного поля имеет следующий вид: при увеличении напряженности сначала она отрицательна, затем проходит через нуль, достигает максимума, после чего существенно уменьшается. В работе установлено, что время релаксации из измерений эллиптичности ультразвука может быть определено по простой формуле

(16)

где п - номер резонанса, как правило, п = 1; - поле резонанса, где - значение напряженности поля, где эллиптичность имеет максимум, - циклотронная масса. Этот метод может применяться, если ультразвук распространяется вдоль кристаллографической оси не ниже третьего порядка. Процесс контроля будет включать цикл охлаждения объекта контроля, измерение и согревание. Поэтому производительность контроля будет низкой. Существуют ограничения в размерах проверяемых объектов. Поэтому можно заключить, что организация неразрушающего контроля особо чистых образцов металлов целесообразна в случаях работы проверяемых объектов в дорогостоящих и не допускающих отказов устройствах.

23

В четвертой главе изложены сложные теоретические вопросы формулировки граничных условий, отражения и преломления волн на границах сред с учетом упругой анизотропии и магнитной поляризации сред. Специальное внимание уделено вопросу о критических углах для волн разной поляризации в упруго анизотропных средах. Детально изучены явления отражения и преломления на границе аустенитной стали в модели трансверсально-изотропной среды. Эта часть работы, базирующаяся как на оригинальных результатах, так и на обобщении известных опубликованных результатов, имеет практическое значение для разработки методик УЗ контроля аустенитной стали.

В пятой главе рассмотрено отражение и преломление волн в неоднородной упругоанизотропной среде. Разработка новых методик ультразвукового контроля имеет особо важное значение для анизотропных, текстурованных или неоднородных материалов. Для повышения надежности и достоверности контроля нужно учесть особенности упругих свойств материала, наиболее существенные для свойств УЗ волн и выявления дефектов. Определение этих существенных особенностей упругих свойств сред составляет основную задачу моделирования для УЗ контроля. Реалистичная модель аустенитного сварного шва должна учитывать пространственную неоднородность среды. Сложность решения задач теории упругости состоит в усложнении вида уравнения эластодинамики в неоднородной среде. В общем виде, при произвольном характере неоднородности, решение уравнений теории упругости не получено. Из литературы известно, что применительно к распространению ультразвука в сварных швах из аустенитной стали построено численное решение задачи о распространении пучка упругих волн в шве с учетом поворота оси кристаллитов, а также рассмотрены явления на границе шва при разных значениях угла падения.

В пятой главе рассмотрен случай среды, неоднородность которой зависит от одной координаты, перпендикулярной плоскости границы. Решения задачи теории упругости получены здесь для системы плоскопараллельных слоев, а также для непрерывно-слоистой среды с несколькими специальными видами неоднородности. Слоистая среда является лишь грубым приближением к реальной структуре материала сварного шва. Задача об отражении поперечных волн слоем с включениями цилиндрической формы может быть решена методами теории рассеяния. Введение тензора обобщенного импеданса для неоднородной среды позволяет определить пути решения задач теории упругости для анизотропных и гиротропных сред.

Рассмотрим прохождение продольных упругих волн через слой трансверсально-изотропного материала. Пусть из жидкой среды на слой толщиной d падает плоская волна, потенциал скорости которой

25

Свойства упругих волн в изотропных неоднородных средах достаточно хорошо изучены. Однако для аустенитного материала мы имеем дело с сочетанием двух важных факторов - упругой анизотропии и неоднородности. Рассмотрим коэффициент прохождения продольных волн через пластину ТИ аустенита, помещенную в жидкость. Ось ТИ среды перпендикулярна плоскости пластины, и параметры пластины изменяются вдоль той же оси. Таким образом, рассматриваемая модель включает такие явления, как интерференция волн в пластине, преобразование типов волн, различие в направлениях фазовой и групповой скоростей, наличие критических углов, рефракция волн. В данной части работы рассмотрена, в частности, реалистичная модель, описывающая переходную зону между трансверсально - изотропным и изотропным аустенитом, включающая в рассмотрение изменение и упругих модулей, и плотности среды. Изучено влияние абсолютного изменения модулей в широких пределах, и скорости изменения. Особое внимание уделено большим углам падения, где прохождение возможно только в анизотропной среде. Специально рассмотрен случай малой толщины, когда возможно количественное сравнение однородной и неоднородной пластин.

Сформулируем результаты относительно упругих волн в ТИ среде, моделирующей аустенитную сталь. Пусть в анизотропной и неоднородной среде распространяется упругая волна

(25) где А - амплитуда, - единичный вектор поляризации, - волновой вектор,

- круговая частота. Движение элемента объема упругой среды должно удовлетворять уравнению теории упругости

(26)

26

где 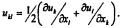Первое слагаемое в правой части (26) учитывает

неоднородность среды. Уравнение (26) нужно дополнить граничными условиями, связывающими упругие смещения и напряжения на границе между средами 1 и 2. На границе упругие смещения и нормальные компоненты напряжений непрерывны,

Если в среде существуют границы раздела, то следует учитывать преобразование типов волн при отражении и преломлении ультразвука. Напряжения могут быть найдены как производные свободной энергии Е по компонентам тензора деформаций

В трансверсально - изотропном твердом теле разложение для свободной энергии с учетом членов не выше второго порядка по деформациям имеет вид

Если изменение модулей упругости мало на расстоянии, равном длине волны, то уравнение (26) можно переписать в виде

где - плотность среды. В (30) волновой вектор есть функция координат. Если второе слагаемое в скобках много меньше первого для всех возможных собственных волн, то неоднородная среда будет в упругом отношении близка к однородной. Это утверждение справедливо, если неоднородность среды не приводит к изменению характера собственных упругих волн. Изменение структуры собственных волн возможно, если плоскость, нормальная к границе раздела, имеет точки касания с какой-либо из поверхностей рефракции кристалла аустенита. Поверхности рефракции аустенитной стали для квазипродольной QL и поперечной SH волн выпуклые. Более сложный вид имеет поверхность квазипоперечной волны QSV. Из литературы известно, что наличие у этой поверхности двух общих точек касания с секущей плоскостью определяется выполнением хотя бы одного из трех неравенств. Условия, определяющие тип касания, для кристалла аустенита имеют вид

Каждое из неравенств (31) определяет тип особенностей кривой пересечения поверхности с плоскостью падения, а именно: 1) касательные к поверхности рефракции параллельны оси 2) параллельны оси 3) параллельны прямой вида Подстановка принятых выше численных значений модулей кристалла аустенитной стали показывает, что все

27

три неравенства удовлетворяются. Отсюда, поверхности рефракции аустенита могут иметь особенности всех трех типов.

Решение уравнения теории упругости ищем для пластины, помещенной между двумя жидкими средами 1 и 2. Компоненты упругих смещений имеют вид

Система координат выбрана таким образом, что ось нормальна плоскости пластины, волновой вектор лежит в координатной плоскости Вследствие такого выбора системы координат зависимость от координаты в (32) отсутствует. Компоненты волнового вектора в первой и второй средах определяются так:

где первый индекс i у компоненты обозначает, к какой среде относится j-я компонента волнового числа. Из изотропии жидкости и ТИ среды в плоскости, перпендикулярной оси следует трансляционная инвариантность относительно сдвигов, параллельных оси Отсюда не зависит от Поэтому, падающая из жидкости продольная волна не возбуждает в ТИ среде волну типа SH. Если уравнение эластодинамики в неоднородной среде (26) умножить на , то после преобразования получим

В этом уравнении величина, стоящая в квадратных скобках в левой части пропорциональна плотности упругой энергии, а величина в квадратных скобках в правой части - плотности потока энергии. Проинтегрированная по времени плотность потока энергии через замкнутую поверхность должна обращаться в нуль. Выберем такую поверхность в виде прямоугольной призмы, основания которой находятся по обе стороны пластины. Непосредственное вычисление с учетом вида (32) упругих смещений приводит к соотношению

(33)

где - угол падения волны на пластину, - угол, под которым волна выходит из пластины в среду 2, — плотность и скорость продольных волн в среде 1; - то же в среде 2. В (33) введены коэффициенты прохождения W и отражения V по амплитуде. Соотношение (33) справедливо в отсутствие полного внутреннего отражения.

В реальней среде, обладающей поглощением, компоненты тензора модулей упругости комплексные. Условия, налагаемые на тензор, не допускают произвольных значений мнимых частей компонент модулей. Для получения оценок используем критерий Сильвестра, следующий из положительности

28

потенциальной энергии деформаций. Критерий обеспечивает положительность квадратичной формы

Интегрирование проводится по толщине пластины h. Из (36) следует, что в поглощающей среде В дальнейшем, при проведении численных расчетов, полагаем среды непоглощающими, так что обычное соотношение может быть использовано для расчета коэффициента отражения, по известному коэффициенту прохождения.

Решение уравнения (26) значительно сложнее, чем обычного уравнения эластодинамики в однородной среде. Поэтому возникает идея заменить неоднородную среду слоистой - совокупностью тонких слоев, причем в пределах каждого среду можно считать однородной. Слоистая среда должна быть выбрана таким образом, что слои в каждой точке локально перпендикулярны вектору градиента скорости волны. Эту замену сред применим к нашей модельной системе: пластине ТИ аустенита, помещенной в жидкость. Ось ТИ среды нормальна плоскости пластины. Скорость упругих волн изменяется вдоль той же оси, из-за неоднородности модулей или плотности. Схема хода лучей в неоднородной пластине показана на рис.7.

29

Алгоритм численного расчета коэффициента прохождения через пластину ТИ среды состоит в следующем. Записываются выражения для амплитуд с учетом граничных условий при z=0 и z=h, h - толщина пластины. Вычисляется коэффициент прохождения по энергии Т

(37)

Трансверсально - изотропная пластина заменяется набором слоев, в пределах каждого ТИ среда считается однородной. На границе соседних слоев происходит отражение, преломление и трансформация типов волн. Решение уравнений теории упругости ищем в виде плоских волн Характеристическое уравнение имеет вид

Формула (39) определяет области значений параметров, при которых возможно решение (38) в виде однородных плоских волн, а именно, при В принятых допущениях, вне этих областей коэффициент прохождения принимается равным нулю.

После расчета амплитуды волны, прошедшей n-й слой, записываются граничные условия на границе n-го и n+1 -го слоев. Затем процесс нахождения амплитуд повторяется, пока не будет найдено решение для всех N слоев, на которые разбита пластина.

Принятым выше значениям модулей кубического кристалла аустенитной стали соответствуют следующие значения модулей ТИ среды

все величины в (40) приведены в единицах В неоднородной пластине модули упругости изменяются от трансверсально - изотропных до значений модулей однородной изотропной стали. Принята следующая модельная зависимость изменения модулей по координате z

В формуле (41) определяет абсолютную величину изменения, а к - "быстроту", с которой модули изменяются по координате z. В расчетах принято, что модули различные в ТИ и изотропной средах, изменяются по закону (41), модули 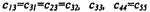остаются постоянными. В большинстве расчетов принято, что плотность ТИ среды р=7,8 г/см3, за исключением раздела, где рассматривается пластина с изменяющейся по толщине плотностью.

30

Максимальное значение производной модуля упругости по координате

Замена неоднородной ТИ среды набором однородных пластин безусловно оправдана, если пластин будет так много, что второе слагаемое в скобках в (30)

будет пренебрежимо мало по сравнению с первым, то есть

учетом (30) получаем условие для минимального допустимого числа слоев N

где - модуль максимального изменения среди всех компонент тензора, дающих вклад в скорость данной собственной волны. В последующих расчетах принято N=200; это обеспечивает точность вычисления коэффициента прохождения не хуже 1%. Далее будут изложены результаты численных расчетов коэффициента прохождения упругих волн через пластину ТИ аустенита. Будет изучено влияние различных факторов на коэффициент прохождения. Сначала приводятся данные расчетов для серии пластин, отличающихся значением коэффициента к в формуле (41), то есть "скоростью" изменения модулей. Затем будет исследовано влияние изменения неоднородности плотности и толщины пластины.

Влияние коэффициента неоднородности. Зависимость коэффициента прохождения от угла падения 0 для пластины толщиной 2,7 мм приведена на рис.8. Здесь и в последующем частота ультразвука принята равной 1 МГц. Пластина погружена в жидкую среду - воду со скоростью волн плотностью 1 г/см3. На рис.8а расчеты приведены для двух значений

коэффициента Из результатов расчетов следует, что величина первого критического угла составляет около