лекции / конспект / DM1

Лекция: Зубчатые цилиндрические передачи.

10.Коэффициент расчетной нагрузки.

11.Условия равнопрочности зубьев по напряжениям изгиба. Особенности расчета передач, работающих в условиях абразивного износа.

12.Особенность расчета косозубых и шевронных цилиндрических передач.

Вопрос 10.

В формулах /6/ и /10/ были введены коэффициенты расчетной нагрузки К_H и К_F, которые учитывают влияние концентрации нагрузки и динамические нагрузки на прочность зубьев. К_H и К_F определяются по аналогичным формулам :

К_H=К_Hβ K_Hv ; K_F = K_Fv K_Fβ /11/

где К_Hβ ; K_Fβ – коэффициенты концентрации наргузки по контактным напряжениям и напряжениям изгиба соответственно. Для понимания физического смысла коэффициента К_β представим следующие схемы положения зубчатых колес:

симметричное несимметричное консольное

Валы под действием сил в зацеплении прогибаются в противоположном направлении. При симметричном расположении перекоса зубчатых колес не наблюдается, при несимметричном и консольном они перекашиваются на угол γ, что приводит к нарушению правильного касания зубьев.

если зубья были абсолютно жесткими, то они касались

только своими концами, т.к. они деформируются, то

нагрузка неравномерно распределяется в соответствии

с деформацией участков зубьев:

К_β= q_max/q_ср

Нагрузка концентрируется на каком-то участке зуба,

что может привести к выламыванию зубьев, поврежде-

нию их поверхности. Для предупреждения этого выполняют колеса со срезанными углами, с НВ ₁ – НВ₂ = 20…50, при высокой твердости зубьям придают бочкообразную форму:

К_β – точное определение значения теоретически

затруднено, поэтому его принимают из таблиц,

полученных на основании исследований и опыта

эксплуатации.

К_Hv , K_Fv – коэффициент динамической нагрузки, учитывает только так называемые внутренние нагрузки, связанные с точностью изготовления зубчатых колес, скоростью движения. Пример: при р_в2› р_в1 , при передаче крутящего момента второе колесо вступит в зацепление в точке а, которая не находится на линии

зацепления А₁А₂ .В точке а происходит так

называемый кромочный удар, который не

только увеличивает динамическую нагрузку

но также способствует задиру поверхности.

Для избежания этого зубья фланкируют – верхний участок эвольвенты выполняют с отклонением в тело зуба. Расчет К_v весьма затруднен, поэтому его также выбирают из таблиц.

Вопрос 11.

При расчете зубьев по напряжениям изгиба в формуле /10/

σ_F= Y_FF_tK_F/(bwm) был введен безразмерный коэффициент Y_F, значение которого зависит от числа зубьев z и x – коэффициента смещения исходного контура. Влияние x на размеры зуба в опасном сечении были рассмотрены в вопросе 4. Влияние числа зубьев на форму зуба иллюстрируется следующим рисунком:

очевидно, что при нарезании разного числа зубьев ширина зуба в опасном сечении будет различной и учитывается коэффициентом Y_F. Т.к. значение допускаемых наряжений изгиба [σ_F1] зависит от НВ, которая принимается различной для зубьев шестерни и колеса , то и [σ_F1] будет отличаться от [σ_F2], причем [σ_F1] › [σ_F2]. В то же время зубья шестерни будут иметь ширину опасного сечения меньше, чем у колеса, то есть они будут слабее работать на изгиб.

Исходя из всего сказанного, существует необходимость производить сравнительную оценку прочности на изгиб зубьев шестерни и колеса по зависимости:

Y_F1[σ_F1] › ‹ Y_F2[σ_F2]

Сравнивая полученные значения неравенства, делают вывод, что следует проверять на изгиб: зубья колеса или шестерни.

Особенностями расчета передач, работающих в условиях абразивного износа, является то, что зубья таких передач (чаще всего открытых передач) обычно рссчитывают только по напряжениям изгиба. При проектном расчете открытых передач определяют модуль зацепления m. Значения m определяют из формулы /10/ путем ее преобразования. При этом числом зубьев z₁ следует задаться :z₁ ≥ 22 (исходя из опыта эксплуатации), m ≥ 5 мм. Проверочный расчет передач определяют по формуле /6/ , то есть по контактным напряжениям.

Вопрос 12.

У косозубых передач зубья располагаются не по образующей делительного цилиндра, а составляют с ней некоторый угол β:

Профиль косого зуба в опасном сечении n –n совпадает с профилем прямого зуба. Модуль в этом сечении стандартный (m_n). В торцовом сечении t–t параметры косого зуба изменяются от угла β. Окружной шаг р_t=p_n/cosβ Делительный диаметр d₁=m_tz₁=m_nz₁/cosβ.Прочность косого зуба определяют его размеры в нормальном сечении. Форму косого зуба принято определять через параметры эквивалентного прямозубого колеса.Нормальное к зубу сечение – это эллипс с полуосями. В зацеплении

В зацеплении участвуют зубья, расположенные на малой оси эллипса (т.к.с=d₂/2). В соответствии с этим мы можем заменить косозубое колесо прямозубым эквивалентным колесом с d_v=d/cos²β (r_v=r/cos²β). Используя вышеизложенные зависимости, можем получить : d_v=1.13d , z_v=d_v/m_n =z/cos²β = 1.2z (при β=20^о). Вследствие наклона зубьев (эквивалентное цилиндрическое колесо больше косозубого) получается, что нагрузка может передаваться косозубым колесом меньших размеров. Косозубая передача прочнее прямозубой, у нее более плавная работа, она менее шумна.

Коэффициент торцового перекрытия.

В отличие от прямых косые зубья входят в зацепление не сразу по всей длине, а постепенно в направлении от точки 1 к точке 2:

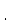
Расположение контактных линий в поле косозубого зацепления изображено в сечении А-А. При вращении колес линии контакта перемещаются в поле зацепления в направлении, показанном стрелкой. Пара 2 зацепляется по всей длине, а пары 1 и 3 лишь частично. Когда пара 3 выходит из зацепления и нахо-дится в положении 3^/, в зацеплении остались две пары: 1^/ и2^/.В отличие от прямозубого косозубое зацепление не имеет зоны однопарного зацепления, зубья нагружаются постепенно.Коэффициент торцового перекрытия:

ε_α=[1.88-3.2(1/z₁+_ 1/z₂)]cosβ

Определение Z_Hβ : Z_Hβ=√K_Hαcos²β/ε_α , где К_Hα –коэффициент неравномерности нагрузки одновременно зацепляющихся пар. В косозубых передачах теоретически зацепляются одновременно не менее двух пар зубьев. Но ошибки нарезания могут устранить двухпарное зацепление, и при контакте одной пары между зубьями второй пары образуется зазор (очень малый), который все же устраняется вследствие упругих деформаций зубьев. Тем не менее нагрузка уже распределяется неравномерно

Z_Fβ=K_FαY_β/ε_α K_Fα тот же смысл, что и для K_Hα .Коэффициенты K_Hα и K_Fα определяются по таблицам в зависимости от степени точности и окружной скорости.

Y_β= 1 – β^o/140 – коэффициент, учитывающий повышение изгибной прочности вследствие наклона контактной линии к основанию зуба:

Y_β – определяем экспериментально при β ≤ 40^о.

В косозубой передаче силы, действующие в

зацеплении раскладывают на три составляющие:

F_t=2T₁/d₁ ; F_a=F_ttgβ ; F_r=F_t^/tgα = F_ttgα/cosβ

где F_t^/ - окружная сила в сечении n-n.

Наличие в зацеплении осевой силы дополнительно нагружает передачи, что является недостатком, который может устраняться

применением шевронных передач. β = 8…18^о – косозубые , β = 30…40^о – шевронные.Расчет по контактным напряжениям σ_H^к = Z_Hβσ_H ≤ [σ_H] , σ_H – по формуле /6/. Расчет по напряжениям изгиба σ_F^K = Z_Fβσ_F ≤ [σ_F] , σ_F - по формуле /10/.

Z_Hβ ; Z_Fβ – коэффициенты повышения прочности зубьев