Методички к лабораторным работам / Отчет местные сопротивления

Министерство образования РФ

Саратовский государственный технический университет

Балаковский институт техники, технологии и управления

ЛАБОРАТОРНАЯ РАБОТА

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ МЕСТНЫХ

ГИДРАВЛИЧЕСКИХ СОПРОТИВЛЕНИЙ

Выполнил

Принял

Балаково 2003

Ц е л ь р а б о т ы :

Определить коэффициенты сопротивления вентиля, внезапного расширения опытным путем, по теоретическим формулам и сравнить результаты.

ОСНОВНЫЕ ПОНЯТИЯ

Местными называются такие сопротивления, которые оказывают сопротивление свободному движению жидкости за счет какого-либо локального препятствия. В местных сопротивлениях возможны следующие случаи:

1) изменяется величина скорости ( внезапное расширение или внезапное сужение, постепенное расширение или сужение потока жидкости );

2) изменяется направление течения ( резкий или плавный поворот потока жидкости );

3) одновременно изменяется величина скорости и направление течения, иногда неоднократно ( вентили, краны, задвижки );

4) изменяется величина скорости и направление течения за счет деления или слияния потоков жидкости ( тройники, крестовины и т.д.).

В местных сопротивлениях сопротивление движению оказывается на небольшом по протяженности участке, поэтому потерями давления по длине местного сопротивления пренебрегают. За счет резкой деформации потока жидкости, перераспределения скоростей по живому сечению, возникновения водоворотных и вихревых образований в окрестности основного потока, поток теряет часть своей энергии. Потери энергии на местных сопротивлениях, выраженные через скоростной напор, определяются по формуле Вейсбаха

,

где h_i - потери напора на местном сопротивлении, м;

 - коэффициент местного сопротивления, зависит от вида местного сопротивления, геометрических размеров и числа Рейнольдса ;

V - средняя скорость движения жидкости, обычно принимается перед местным сопротивлением, м/с ;

g - ускорение силы тяжести, g = 9,81 м/с².

Коэффициенты местных сопротивлений преимущественно определяются опытным путем. Для характерных местных сопротивлений значения коэффициентов местных сопротивлений приводятся в справочной литературе по гидравлике. В некоторых случаях коэффициент местного сопротивления можно определить теоретически. Рассмотрим случай внезапного расширения потока ( рис.1 ) . Потери напора при внезапном расширении потока определяются по формуле Борда:

или ,

где ₁ - коэффициент Кориолиса в узком сечении трубы;

V₁ - средняя скорость в узкой части трубы;

V₂ - средняя скорость в широкой части трубы;

_в.р - коэффициент местного сопротивления при внезапном расширении потока жидкости, равный

,

где d₁ - диаметр трубы в узкой части;

d₂ - диаметр трубы в широкой части.

В основу формулы Борда положены два существенных допущения:

1) пренебрежение силами внешнего трения на участке между сечениями 1-1 и 2-2;

2) принятие распределения давления в сечении 1-1 по гидростатическому закону.

Учитывая это обстоятельство, необходимо ввести поправочный коэффициент k , тогда

.

Поправочный коэффициент к устанавливается опытным путем.

О п и с а н и е л а б о р а т о р н о й у с т а н о в к и

Схема лабораторной установки приведена на рис.3. Подача воды в напорный бак 3 осуществляется по трубе 1. Подача воды регулируется при помощи вентиля 2. Из напорного бака вода по трубе поступает на местные сопротивления: внезапное расширение трубы 4 и вентиль 8 . До и после местных сопротивлений подключены пьезометры 5 , соединенные с трубой шлангами 7. Показания пьезометров определяются по шкале 6. Расход воды из напорного бака регулируется при помощи вентиля 9. Для измерения расхода воды используется мерный бак 10. Вода из мерного бака сливается по трубе 11 при помощи вентиля 12. Температура воды измеряется термометром 13 .

ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА.

1. Вычисляются площади поперечного сечения трубы в узкой части трубы S₁ и в широкой части трубы S₂ .

2. Вычисляют расход воды Q для каждого опыта.

3. Вычисляется средняя скорость течения воды в узкой и широкой части трубы: .

4. Из приложения в зависимости от температуры воды определяются коэффициенты кинематической вязкости .

5. Вычисляются числа Рейнольдса в узкой и широкой части трубы для каждого опыта , и определяются режимы течения воды. В зависимости от режима течения воды определяется коэффициент Кориолиса:

— при ламинарном течении  = 2 ;

— при турбулентном течении  = 1.05-1.1 .

6. Вычисляются потери напора на внезапном расширении трубы по формуле

.

Потери напора на вентиле равны разности показаний пьезометров, т.к. диаметры труб в месте установки пьезометров одинаковые .

7. Вычисляются коэффициенты сопротивления вентиля из формулы Вейсбаха.

.

8. Вычисляются коэффициенты сопротивления внезапного расширения по опыту

.

9. Вычисляются теоретические коэффициенты сопротивления внезапного расширения

.

10. Определяют поправочные коэффициенты

.

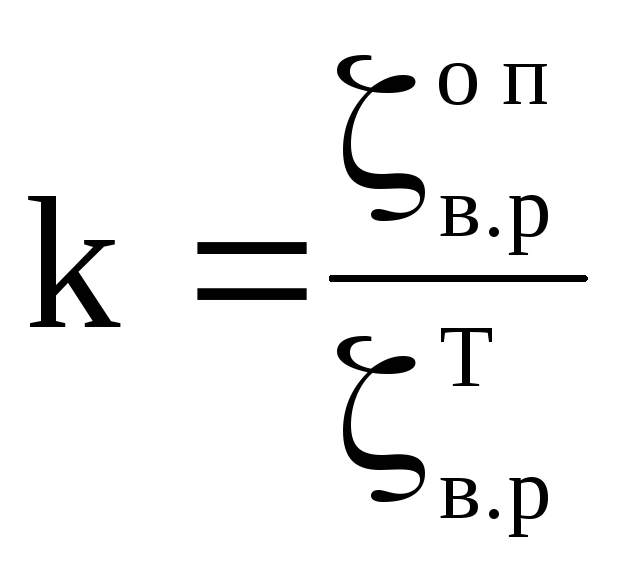КОНТРОЛЬНЫЕ ВОПРОСЫ.

1. От каких факторов зависят потери напора на местных сопротивлениях?

2. Как определяются потери напора на местных сопротивлениях ?

3. От каких факторов зависит коэффициент местного сопротивления ?

4. Как изменяется скорость и давление в потоке жидкости при внезапном расширении трубы ?

5. Как определяются потери напора при внезапном расширении трубы и на вентиле ?

6. Каким способом определяется расход воды при проведении опытов ?

7. По какой формуле определяется средняя скорость потока при обработке результатов?

8. Как определяются опытные значения коэффициентов местных сопротивлений ?

9. Как теоретически вычисляются потери напора на внезапном расширении трубы ?

10. По какой формуле определяются теоретические значения коэффициента сопротивления при внезапном расширении трубы ?

Результаты опытов по определению коэффициентов местных

сопротивлений

№	Наименование	Единица	Номера опытов
	измерений	измерения	1	2	3
1	2	3	4	5	6
	1. Размеры местных сопротивлений
1.1	Диаметр трубы в узкой части , d1	см
1.2	Площадь поперечного сечения трубы , S1	см2
1.3	Диаметр трубы в широкой части , d2	см
1.4	Площадь поперечного сечения трубы , S2	см2
	2. Определение расходов , скоростей и режимов течения
2.1	Заданный объем мерного бака , W	см3
2.2	Время наполнения мерного бака , 	с
2.3	Расход воды , Q	см3/ с
2.4	Средняя скорость до расширения , V1	см / с
2.5	Средняя скорость после расширения , V2	см / с
2.6	Средняя скорость на входе в вентиль , VB	см / с
2.7	Температура воды , t°	° C
2.8	Кинематическая вязкость воды , 	см 2/ c
2.9	Число Рейнольдса в узкой части трубы	-
2.10	Режим течения воды	-
2.11	Коэффициент Кориолиса , 	-
2.12	Число Рейнольдса в широкой части трубы	-
2.13	Режим течения воды	-
2.14	Коэффициент Кориолиса , 	-
	3. Определение потерь напора
3.1	Разность показаний пьезометров
	на внезапном расширении , h	см
3.2	Потери напора на внезапном
	разширении трубы	см
3.3	Разность показаний пьезометров
	на вентиле , hB	см
3.4	Потеря напора на вентиле	см
	4. Коэффициент местных сопртивлений
4.1	Коэффициент сопротивления вентиля , в	-
4.2	Коэффициент сопротивления внезапного
	разширения по опыту , вр	-
4.3	Коэффициент сопротивления внезапного
	разширения теоретически , вр.т	-
4.4	Поправочный коэффициент , k	-

Схема экспериментальной установки

5