Глава 3. Истечение жидкости через отверстия, насадки, дроссели и клапаны

В процессе истечения жидкости происходит преобразова­ние потенциальной энергии жидкости в кинетическую.

Из уравнения Бернулли легко выводится выражение для скорости истечения

, (3.1)

где Н - расчетный напор, который в общем случае равен сумме геометрического и пьезометрического напоров, т.е.

, (3.2)

 - коэффициент скорости, определяемый как

. (3.3)

Здесь  - коэффициент Кориолиса;  - коэффициент мест­ного сопротивления.

Расход жидкости при истечении через отверстия, насадки, дроссели и клапаны определяется произведением скорости истечения на площадь сечения струи. Однако последняя часть бывает меньше площади отверстия вследствие сжатия струи, Поэтому вводится коэффициент сжатия

, (3.4)

где S_c и S₀ - площади сечения струи и отверстия.

Отсюда расход равен

. (3.5)

Вместо расчетного напора Н часто используется расчет­ный перепад давления p=Hg и вместо (3.5) пишут

(3.6)

Истечение жидкости может происходить либо в газовую среду, например в атмосферный воздух, либо в среду той же жидкости, В последнем случае вся кинетическая энергии струи теряется на вихреобразования.

Отверстием в тонкой стенке называется отверстие, диа­метр которого больше толщины стенки и. В этом случае коэффициент расхода  и другие коэффициенты однозначно определяются числом Рейнольдса, а в приближенных расче­тах обычно принимают: ε=0,64; =0,97; =1; ==0,065; =0,62.

При внешнем цилиндрическом насадке, который пред­ставляет собой короткую трубу, приставленную к отверстию снаружи, или при отверстии, диаметр которого d₀ в 2…6 paз меньше толщины стенки , возможны два режима истечения безотрывный и отрывный. Коэффициенты при 1-м режиме в приближенных расчетах обычно принимают ==0,82; =0,5; ε=1.

При 2-м режиме коэффициенты ничем не отличаются от истечения через отверстие в тонком стенке.

Внутренний цилиндрический насадок — это короткая трубка, приставленная к отверстию изнутри. Возможны два режима истечения аналогично предыдущему, но с другими значениями коэффициентов

при 1-м режиме =0,71; =1,0.

при 2-м режиме ≈ε=0,5.

Сопло, или коноидальный насадок, обеспечивают плавное, безотрывное сужение потока внутри насадка и параллельно-струйное точение на выходе. Для сопла в расчетах можно принимать: ==0,97; =0,06.

Диффузорный насадок с закругленным входом, применя­емый в особых случаях, имеет коэффициент расхода, изменя­ющийся в широких пределах в зависимости от угла конусно­сти и степени расширения диффузора. Приближенно ко­эффициент сопротивления  такого насадка может быть определен как сумма коэффициентов сопротивления сопла и диффузора, а коэффициент расхода  можно определить по , положив ε=1.

Указания к решенщо задач

Задачи данного раздела можно решать без записи урав­нения Бернулли. Так, если дана задача на истечение через отверстие, насадок или дроссель (жиклер) и задан коэффици­ент расхода , то следует применить основной выражение (3.5). При этом следует помнить, чти расчетный напор в общем случае складывается из разностей геометрических и пьезометрических высот (3.2).

Следует знать, что коэффициент расхода , однозначно определяется коэффициентами сжатия струи ε и скорости  (или сопротивления ).

Указанное выше основное-выражение для расхода спра­ведливо при истечении через отверстия, насадки и дроссели.

Последние могут иметь форму отверстия или насадка, но всегда истечение через них происходит в среду, заполненную той же самой жидкостью (истечение под уровень). При этом кинетическая энергия, теряемая на вихрообразования, учиты­вается коэффициентом расхода.

Если истечение жидкости происходит при переменном напоре (опорожнение резервуаров), то в каждый данный момент движение жидкости можно рассматривать как уста­новившееся.

ЗАДАЧИ

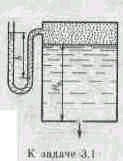
Задача 3.1. Определить расход жидкости (=800кг/м³), вытекающей из бака через отверстие площадью S₀=1см². Показание ртутного прибора, измеряющего давление воздуха, h=268мм, высота H=2 м, Задача 3.1.Определить расход жидкости (р = 800кг/м³ ),вытекающей из бака через отверстие площадьюS₀коэффициент расхода отверстия  = 0,60.

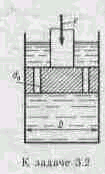
Задача 3.2. Определить скорость перемещения поршня вниз, если к его штоку приложена сила F=10кН. Поршень диаметром D=50 мм имеет пять отверстий диаметром d₀=2 мм каждое. Отверстия рассматривать как внешние цилиндрические насадки с коэффициентом расхода =0,82; =900 кг/м³.

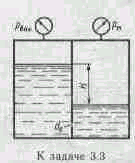
Задача3.3. Определить направление истечения жидкости (=_вод) через отверстие d₀=5 мм и расход, если разность уровней H=2 мм, показание вакуумметра p_вак соответствует 147 мм рт.ст., показание манометра р_м=0,25 МПа, коэффициент расхода =0,62.

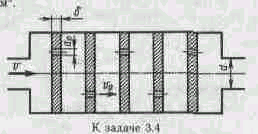
Задача3.4. Определить коэффициент сопротивления многоступенчатого дросселя, отнесенный к скорости в трубке диаметром d=10 мм, если дроссель состоит из пяти ступеней.

Каждая ступень представляет собой отверстие диаметром d₀=2 мм в стенке толщиной  =1,0 мм. Принять коэффициент расхода такого отверстия равным =0,62 и считать, что взаимное влияние ступеней дросселя отсутствует (скорость в промежутках между стенками гасится до нуля), а полная потеря напора распределяется между ступенями поровну. Определить полную потерю давления в дросселе при скорости течения в трубке v=1м/с, если плотность жидкости =850 кг/м³.

Задача3.5. Из резервуара, установленного на полу и заполненного жидкостью до высоты H, происходит истечение жидкости через отверстие в стенке. На какой высоте y должно быть отверстие, чтобы расстояние x до места падения струи на пол было максимальным?

Определить это расстояние. Жидкость считать идеальной.

Задача 3.6. Жидкость вытекает К задаче 3.1.

Доработать

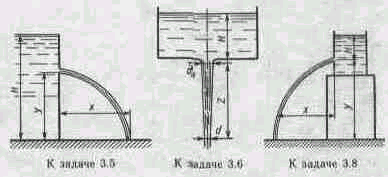
Задача 3.7. При исследовании истечения через круглое отверстие диаметром d ₀ = 10мм получено: диаметр струи d_с =8 мм; напор Н=2 м; время наполнения объема V = 10 л; t = 32,8 с. Определить коэффициенты сжатия ε, скорость φ, расхода μ и сопротивления ζ. Распределение скоростей по сечению струи принять равномерным.

Задача 3.8. При истечении жидкости через отверстие диаметром d₀= 10 мм измерены : расстояние x = 5,5 м, высота y = 4 м, напор Н = 2 м и расход жидкости Q =0,305 л/с. Подсчитать коэффициенты сжатия ε, скорости φ, расхода μ и сопротивления ζ. Распределение скоростей по сечению струи считать равномерным.

Сопротивлением воздуха пренебречь.

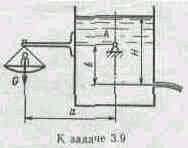
Задача 3.9. На рисунке показана схема устройства для исследования истечения через отверстия и насадки. Резервуар с жидкостью укреплен на двух опорах A и имеет возможность покачиваться в плоскости чертежа. При истечении из отверстия или насадка сила реакции струи выводит резервуар из положения равновесия, однако груз весом G возвращает его в это положение. Подсчитать коэффициенты сжатия струи ε, скорости φ, расхода μ и сопротивления ζ при истечении воды, если известны размеры а = 1 м, b = 1 м, диаметр отверстия d₀ = 10 мм. При опыте измерены: напор H = 2м, расход Q= 0,305 л/с и вес груза G = 1,895 H. Распределение скоростей в сечении струи принять равномерным.

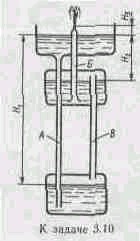
Задача 3.10. На рисунке изображена схема устройства, известного под названием «Геронов фонтан». Трубы A и Б заполнены водой, а труба В – воздухом. Объяснить принцип действия и

Доработать

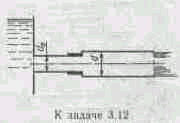
V₀₌0в обоих случаях. Диаметр выходного канала сопла d==2мм; а коэффициент расхода ==0,85.

Чему было бы равно отношение сил F₂/F₁ в двух случаях при отсутствии потерь напора в сопле?

Указание. Во 2-м случае следует записать уравнение количества движения в направлении струи.

`

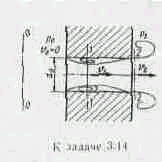
Задача 3.14. Через жиклер, представляющий собой отверстие диаметром d₀₌2мм в стенке толщиной =5мм, происходит истечение жидкости в полость жидкости в полость, заполненную той же жидкостью при избыточном давлении р₂=1МПа. Определить давление по другую сторону стенки р_0,при котором внутри жиклера возникает кавитация. Давление насыщенных паров жидкости соответствует h_н.п==60 мм рт.ст., =850 кг/м³. Коэффициент сжатия струи внутри жиклера принять равным =0,64; коэффициента расхода , равным коэффициенту скорости, ==0,82.

Какой будет расход Q при начале квитанции?

Указание. Следует записать уравнение Бернулли для сечения 1-1 и 2-2, при этом учесть потерю напора на внезапное расширение по теореме Борда и использовать уравнение расхода.

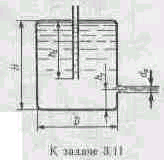
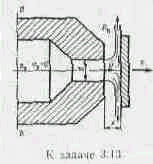
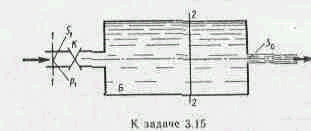
Задача 3.15. Вода под избыточным давлением p₁=0,3Мпа подается по трубе с площадью поперечного сечения S₁=5см² к балону Б , заполненому водой . На трубе перед баллоном установлен кран К с коэффициентом местного сопротивления =5. Из баллона Б вода вытекает в атмосферу через отверстие площадью S₀₌1см²; коэффициент расхода отверстия равен =0,63. Определить расход воды Q.

Указание. Записать уравнение Бернулли для сечений 1-1 и 2-2 и основную формулу для расхода при истечении.

Задача 3.16. Дан диффузорный насадок с плавно закруглённым входом в виде сопла ( =0,06) и диффузора с оптимальным углом конусности (=5⁰30^/) и с соотношением диаметров D₂/D₁=3,для которого можно принять коэффициент сопротивления =0,125. Коэффициенты сопротивления отнесены к узкому сечению. Определить для данного насадка коэффициент , отнесенный к площади выходного отверстия (D₂) , и коэффициент расхода ^/, отнесённый к площади узкого сечения (D₁).