Расчет контура регулирования
4. Расчет контура регулирования
Стабилизатор бензина К-304 представляет собой тарельчатую ректификационную колонну, которая служит для разделения жидких однородных смесей на составляющие вещества в результате противоточного взаимодействия смеси паров и жидкой смеси.
Выделим основные возмущения, возможные регулирующие воздействия и выходные координаты.
Поскольку исходная смесь поступает в ректификационную колонну из предыдущих аппаратов технологической линии, колебания расхода, состава и температуры питания являются основными возмущениями в процессе ректификации. Из перечисленных возмущений стабилизируют обычно только температуру питания, расход питания контролируют, состав питания контролируют в редких случаях. К регулирующим воздействиям в данном случае можно отнести расход дистиллята, расход кубового продукта и расход флегмы. К выходным переменным отнесем уровень в кубе колонны, давление в колонне и состав продукта. Наибольшей чувствительностью по отношению к возмущениям и к регулирующим воздействиям обладают промежуточные тарелки в верхней и нижней части колонны, называемые контрольными тарелками. По отношению к возмущениям со стороны питания составы на контрольных тарелках являются промежуточными координатами и обладают меньшей инерционностью, чем составы продуктов. Поэтому составы на контрольных тарелках часто используют в качестве регулируемых координат вместо составов продуктов.
Структурная схема объекта
Рис. 4.1. Структурная схема объекта
В данном проекте сравниваются различные характеристики каскадной и одноконтурной систем регулирования концентрации верха стабилизатора бензина К-304.
4.1. Математическая модель.
Допущения:
1. на каждой тарелке – идеальное смешение;
2. смесь содержит только два компонента;
3. жидкость поступает на тарелку питания при температуре кипения;
4. давление по высоте колонны не меняется;
5. жидкость на каждой тарелке находится при температуре кипения, а пар при температуре конденсации. В этом случае температура жидкости будет определяться составом смеси (из справочника). Тепловой баланс составлять не нужно.
6. теплообменом с окружающей средой пренебрегаем;
7. количество тепла, требуемого для испарения 1 моля легколетучего компонента ≈ равно количеству тепла требуемого для конденсации 1 моля тяжелолетучего компонента. В этом случае число молей легколетучего компонента, которое перейдёт из жидкости в пар на каждой тарелки, равно числу молей тяжелолетучего компонента, которое перейдёт из пара в жидкость на этой же тарелки. Такой массообмен называется эквимолярным.
8. мольные расходы жидкости и пара по высоте колонны постоянны;
9. вес жидкости на тарелках одинаков;
10. концентрация легколетучего в паре равна концентрации его же на тарелках;
11. при конденсации пара в дефлегматоре состав смеси не меняется, при испарении смеси в кубе её состав тоже не меняется;
12. в рассматриваемом диапазоне изменения концентраций содержание легколетучего компонента в паре является линейной функции от концентрации легколетучего компонента в жидкости.
Структурная схема колонны:
Структурная схема колонны представляет собой последовательность апериодических звеньев.
Вывод передаточных функций:
Для нижней тарелки:
Запишем материальный баланс для концентрации на нижней тарелке:
y=C0-C*
Преобразуем по Лапласу:
Передаточная функция для нижней тарелки будет выглядеть следующим образом:
,
где
.
Для первой тарелки:
Запишем материальный баланс для концентрации на первой тарелке:
Преобразуем по Лапласу:
Передаточная функция для первой тарелки будет выглядеть следующим образом:
,
где
.
Для второй тарелки:
Запишем материальный баланс для концентрации на второй тарелке:
Преобразуем по Лапласу:
Передаточная функция для второй тарелки будет выглядеть следующим образом:
,
где
.
Для верхней тарелки:
Запишем материальный баланс для концентрации на верхней тарелке:
Преобразуем по Лапласу:
Передаточная функция для верхней тарелки будет выглядеть следующим образом:
,
где
.
Определение численного вида передаточных функций
Исходные регламентные данные:
Fk=0,610 м3/мин.
FD=0,390 м3/мин.
L=0,577 м3/мин.
V=1,154 м3/мин.
D=3.8 м – диаметр колонны
Построение кривой фазового равновесия:
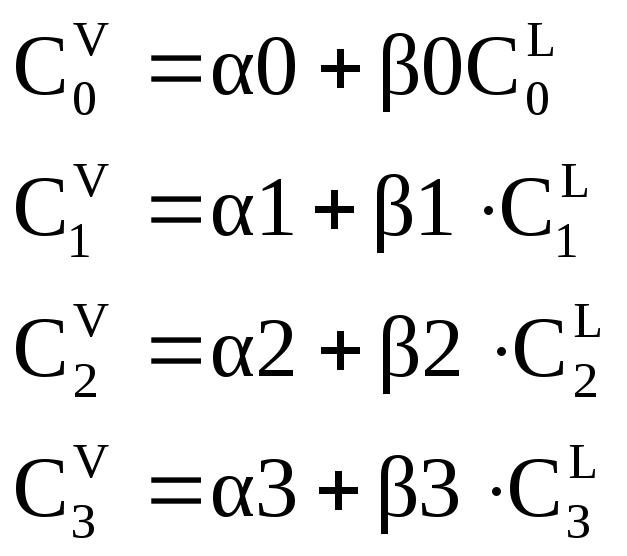
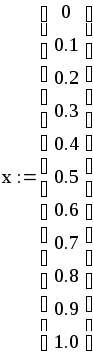
На кривой фазового равновесия строятся касательные к точкам, которые соответствуют 0, 1, 2, 3 тарелкам. Через уравнения этих касательных определяются коэффициенты α и β.
g0, g1, g2, g3 – весовые коэффициенты
gк= Sпл h=11.3*0.1=1.13 м3 - для первой, второй и верхней тарелок;
gк=0.5Sпл+0.5 V= 20 м3 - для нижней тарелки.
- ПФ для нижней тарелки
- ПФ для первой тарелки
- ПФ для второй тарелки
где
- ПФ для верхней тарелки
Передаточная функция колонны выглядит следующим образом:
Wкол= W1W2W3W4
