2.4 Характеристики чувствительности средств измерений к влияющим величинам. Неинформативные параметры выходного сигнала

Влияние, оказываемое внешними факторами, описывается при помощи следующих характеристик.

Функция влияния () - это зависимость изменения MX СИ от изменения влияющей величины или их совокупности в рабочих условиях применения СИ. Использование функций влияния позволяет определить не предельно возможные значения погрешности, практически не встречающиеся при исправных СИ, а их статистические оценки. Нормирование функции производится путем установления ее номинального значения и пределов допустимых отклонений от него. Возможно нормирование граничных, верхней и нижней функций влияния.

Изменения значений метрологических характеристик СИ, вызванные изменениями влияющих величин в установленных пределах. () - это разность (без учета знака) между MX, соответствующей некоторому заданному значению влияющей величины  в пределах рабочих условий применения СИ, и данной MX, соответствующей нормальному значению влияющей величины. Эти изменения нормируются путем установления пределов допускаемых изменений характеристики при изменении влияющей величины в заданных пределах.

2.5 Нормирование динамических характеристик средств измерений

Для описания динамических погрешностей используются следующие характеристики:

1. Полная динамическая характеристика аналоговых СИ, в качестве которой используют одну из характеристик: переходную, импульсную переходную, амплитудно-фазовую, амплитудно-частотную, совокупность амплитудно-частотной и фазочастотной, передаточную функцию.

2. Частные динамические характеристики аналоговых СИ, которые можно использовать как линейные. К ним относятся время реакции, коэффициент демпфирования, постоянная времени и др.

3. Частные динамические характеристики АЦП и цифровых измерительных приборов. К ним относятся время реакции, погрешность датирования отсчета, максимальная частота измерений и др.

2.6 Метрологические характеристики влияния на инструментальную составляющую погрешности измерения

- входной импеданс

- выходной импеданс

52, Комплексы нормируемых метрологических характеристик средств измерений

Большое разнообразие групп СИ делает невозможной регламентацию конкретных комплексов MX для каждой из этих групп в одном нормативном документе. В то же время все СИ не могут характеризоваться единым комплексом нормируемых MX, даже если он представлен в самой общей форме.

Всю совокупность MX можно разбить на две большие группы. В первой из них инструментальная составляющая погрешности определяется путем статистического объединения отдельных ее составляющих. При этом доверительный интервал, в котором находится инструментальная погрешность, определяется с заданной доверительной вероятностью меньше единицы. Для MX этой группы принята следующая модель погрешности в реальных условиях применения (модель 1): , где - систематическая составляющая; - случайная составляющая; - случайная составляющая, обусловленная гистерезисом; - объединение дополнительных погрешностей; - динамическая погрешность; l - число дополнительных погрешностей, равное числу всех величин, существенно влияющих на погрешность в реальных условиях. В зависимости от свойств СИ данного типа и рабочих условий его применения отдельные составляющие могут отсутствовать.

Первая модель выбирается, если допускается, что погрешность изредка превышает значение, рассчитанное по нормируемым характеристикам. При этом по комплексу MX можно рассчитать точечные и интервальные характеристики, в которых инструментальная составляющая погрешности измерений находится с любой заданной доверительной вероятностью, близкой к единице, но меньше ее.

Для второй группы MX статистическое объединение составляющих не применяется. К таким СИ относятся лабораторные средства, а также большинство образцовых средств, при использовании которых не производятся многократные наблюдения с усреднением результатов. Инструментальная погрешность в данном случае определяется как арифметическая сумма наибольших возможных значений ее составляющих. Эта оценка дает доверительный интервал с вероятностью, равной единице, являющийся предельной оценкой сверху искомого интервала погрешности, охватывающего все возможные, в том числе весьма редко реализующиеся, значения. Это приводит к существенному ужесточению требований к MX, что может быть применимо только к наиболее ответственным измерениям, например, связанным со здоровьем и жизнью людей, с возможностью катастрофических последствий неверных измерений и т.п.

Арифметическое суммирование наибольших возможных значений составляющих инструментальной погрешности приводит к включению в комплекс нормируемых MX пределов допускаемой погрешности, а не статистических моментов. Это допустимо также для СИ, имеющих не более трех составляющих, каждая из которых определяется по отдельной нормируемой MX. В этом случае расчетные оценки инструментальной погрешности, полученные арифметическим объединением наибольших значений ее составляющих и статистическим суммированием характеристик составляющих (при вероятности, хотя и меньшей, но достаточно близкой к единице), практически различаться не будут.

Для рассматриваемого случая модель 2 погрешности СИ:

.

Здесь - основная погрешность СИ без разбиения ее на со-

ставляющие (в отличие от модели 1). Модель 2 применима только для тех СИ, у которых случайная составляющая пренебрежимо мала.

Вопросы выбора MX достаточно детально регламентированы в ГОСТ 8.009-84, где приведены характеристики, которые должны нормироваться для названных выше групп СИ. Приведенный перечень может корректироваться для конкретного средства измерений с учетом его особенностей и условий эксплуатации. Важно отметить, что не следует нормировать те MX, которые оказывают несущественный по сравнению с другими вклад в инструментальную погрешность.

Расчет погрешностей средств измерений по нормированным метрологическим характеристикам

Расчет инструментальной погрешности в силу ее случайности сводится к нахождению интервала, в котором она находится с заданной вероятностью Р. Определение интервала осуществляется в три этапа.

На первом этапе вычисляются математическое ожидание и дисперсия каждой из четырех составляющих погрешности. Для основной погрешности вид расчетных формул зависит от того, какие MX нормированы. Если заданы нормированные значения и = систематической составляющей, то характеристики основной погрешности имеют вид: ; ,

где . Если нормированы пределы допускаемой систематической погрешности , то ; .

Если же нормированы пределы допускаемой основной погрешности то в предположении равномерного распределения значений по­грешности для совокупности СИ данного типа имеем ; ;

Для определения характеристик дополнительной погрешности необходимо знать не только нормированные функции влияния , но и статистические характеристики влияющих величин . От того, какие характеристики в реальных условиях применения СИ известны, зависит достоверность получаемых оценок инструментальной составляющей. Если для СИ нормированы функции

влияния каждой влияющей величины отдельно, то ; ; 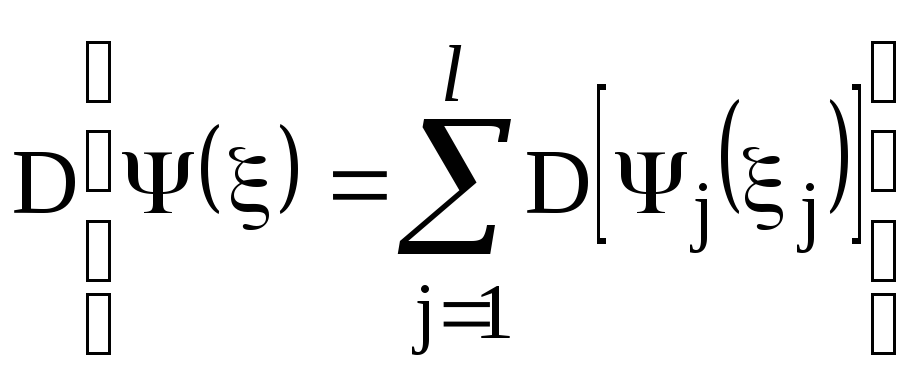где l — число внешних влияющих величин.

Если же для СИ нормирована функция совместного влияния нескольких величин , то ее математическое ожидание и дисперсию находят по известным правилам определения статистических характеристик функций нескольких случайных величин.

Математическое ожидание и дисперсия динамической погреш­ности могут быть оценены путем анализа формул, выражающих связь значений погрешностей с параметрами измеряемого сигнала и нормированными динамическими характеристиками СИ.

На втором этапе производится оценка инструментальной по­грешности , обусловленной взаимодействием СИ с объектом измерений. Она существенным образом зависит от характера этого взаи­модействия и вида импедансной характеристики.

После определения характеристик всех ее составляющих произ­водится расчет таких же характеристик инструментальной погреш­ности путем сложения найденных математических ожиданий и дисперсий соответственно.

На третьем этапе производится оценка интервала, в котором с доверительной вероятностью Р находится инструментальная погрешность измерения: , где К - коэффициент, зависящий от вида закона распределения инструментальной погрешности и заданной доверительной вероятности. Наиболее распространенным является значение коэффициента К= 2,0 , что соответствует доверительной вероятности 0,95.