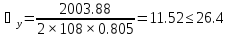- •Компоновка балочной клетки.
- •Компоновка конструкций балочной клетки.
- •1.2. 1.Расчёт стального листового настила.
- •1.3 Расчет прокатных балок
- •2. Расчет и конструирование главной балочной клетки.
- •2.1 Подбор сечения главной балки.
- •2.2 Изменение сечения по длине.
- •Расчетная схема
- •Изменение ширины пояса по длине балки
- •2.3 Расчет местной устойчивости стенки балки.
- •2.4 Монтажный стык балки
- •2.5. Узел сопряжения балок.
- •Примыкание к дополнительному ребру.
- •3. Расчет поддерживающих колонн.
- •3.1 Определение нагрузки на колонну.
- •3.2. Определение расчётной длины колонны.
- •3.3 Подбор сечений стержня колонны.
- •3.4 Расчет и конструирование оголовка колонны.
- •3.5. Расчёт и конструирование базы колонны.
2.5. Узел сопряжения балок.
Балки к рёбрам крепим болтами нормальной точности, а затем обвариваем (рисунок 2.13.) Сечение дополнительных рёбер принимаем аналогично сечению рёбер жёсткости:
Ширина
выступающей части ребра:
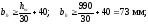
Толщина
ребра:

По
сортаменту на листовую сталь принимаем
полосу шириной
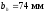 и толщиной
и толщиной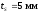
Количество болтов, необходимое для закрепления балки :
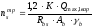 ;
;
где К =1,1 - при креплении с односторонней накладкой
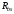 -
расчётное сопротивление болтов на срез,
-
расчётное сопротивление болтов на срез,
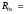 190
МПа = 19 кН/см2
.
190
МПа = 19 кН/см2
.
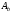 -
площади сечения болта ,
-
площади сечения болта ,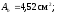
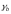 =
0,9 - коэффициент условия работы соединения.
(по СНиП, для высокопрочных болтов)
=
0,9 - коэффициент условия работы соединения.
(по СНиП, для высокопрочных болтов)
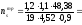 0,82
0,82
 2;
2;
Поверяем принятое количество болтов на смятие соединяемых элементов:
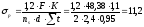 см
см
где d – наружный диаметр стержня болта, d = 24 мм,
Сварку производят электродами Э 42 с Rwf = 180 МПа. Принимаем катет шва Кf = 3 мм и находим необходимую длину шва.
Находим необходимую длину ребра из условия его работы на срез:
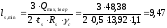 см
см
Необходимая длина шва крепления дополнительного ребра к стенке балки:
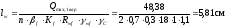
Принимаем длину дополнительных рёбер равную 30 см.
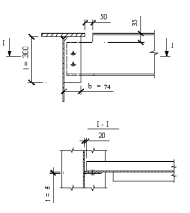
Рисунок 2.13. Узел сопряжения балок,
Примыкание к дополнительному ребру.
3. Расчет поддерживающих колонн.
Поддерживающие колонны балочного перекрытия работают на центральное сжатие.
Центрально-сжатая колонна, как конструктивный элемент состоит из: оголовка, воспринимающего нагрузку от вышележащих конструкций; стержня, передающего нагрузку от оголовка к базе; базы.
Далее веду расчет стержня колонны сплошного составного двутаврового сечения.
3.1 Определение нагрузки на колонну.
Нагрузка передается в виде опорных реакций вышележащих конструкций.
Для расчета принимаю центральную колонну как наиболее нагруженную. Нагрузка равна:
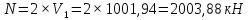
3.2. Определение расчётной длины колонны.

Расчётная длина колонны постоянного сечения:
 ,
где
,
где
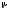 —коэффициент
расчётной длины, вычисляемый в зависимости
от условий закрепления концов колонны
и характера нагрузки. Для заданной
колоны принимаем схему закрепления,
показанную на рис. 22, при которой
коэффициент
—коэффициент
расчётной длины, вычисляемый в зависимости
от условий закрепления концов колонны
и характера нагрузки. Для заданной
колоны принимаем схему закрепления,
показанную на рис. 22, при которой
коэффициент
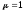
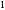 —геометрическая
длина колонны, равная расстоянию между
точками закрепления колонны от поперечного
смещения.
—геометрическая
длина колонны, равная расстоянию между
точками закрепления колонны от поперечного
смещения.
Принимаем:
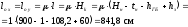
где — отметка верха настила (по заданию
— отметка верха настила (по заданию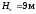 );
);
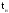 —толщина
настила (см. подраздел 1.2.)
—толщина
настила (см. подраздел 1.2.)
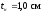
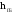 —высота
главной балки с учётом опорного ребра
—высота
главной балки с учётом опорного ребра
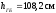
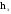 —заглубление
колонны от уровня пола (отм. 0.000) до
подошвы опорной плиты базы фундамента.
Принимаем
—заглубление
колонны от уровня пола (отм. 0.000) до
подошвы опорной плиты базы фундамента.
Принимаем
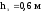
3.3 Подбор сечений стержня колонны.
В случае центрально-сжатой сквозной колонны воспринимаемое усилие равномерно распределяется на обе ветви. Отсюда требуемая площадь ветви колонны из условия устойчивости:
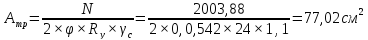
Где:
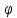 – коэффициент продольного изгиба
центрально-сжатого элемента
– коэффициент продольного изгиба
центрально-сжатого элемента
Для
определения
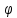 предварительно задаюсь гибкостью
предварительно задаюсь гибкостью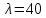 .
Сечение колонны принимаю по сортаменту
из условия требуемой площади :
.
Сечение колонны принимаю по сортаменту
из условия требуемой площади :
Принимаю двутавровую колонну 30К1 по сортаменту:
Характеристики:
Wx = 1223 см3
Ix = 18110 см4
t = 9 мм
qгп = 65,2 кг/м
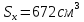
h = 296 мм
b= 300 мм
A=108
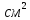
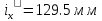
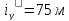 проверяю
принятое сечение относительно оси (ось
Х) на гибкость:
проверяю
принятое сечение относительно оси (ось
Х) на гибкость:
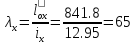
где
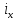 – радиус инерции сечения колонны
относительно материальной оси(оси
Х),равный радиусу инерции ветви
относительно тойже оси.
– радиус инерции сечения колонны
относительно материальной оси(оси
Х),равный радиусу инерции ветви
относительно тойже оси.
Условие устойчивости относительно материальной оси (оси Х):
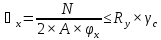
где:
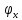 -
коэфициэнт продольного изгиба ,
определяемый в зависимости от
-
коэфициэнт продольного изгиба ,
определяемый в зависимости от
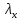
А- площадь сечения одной ветви.
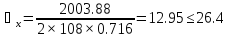
Для проверки сечения относительно оси(оси У) необходимо определить растояние между ветвями, которое определяеться из условия равноустойчивости колонны относительно обеих осей:
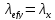
где
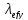 -
приведенная гибкость сечения относительно
свободной оси (оси У)
-
приведенная гибкость сечения относительно
свободной оси (оси У)
Гибкость сечения относительно свободной оси У:
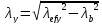 =
=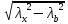 =
=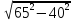 =51.23
=51.23
где
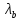 -
гибкость ветви относительно оси У на
растоянии между планками, ее значение
задают из следующих условий:
-
гибкость ветви относительно оси У на
растоянии между планками, ее значение
задают из следующих условий:
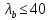
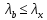
Растояние между центрами ветвей:
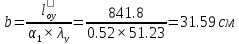
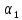 -
для ветвей из двутавров равен 0,52
-
для ветвей из двутавров равен 0,52
Просвет между ветвями:
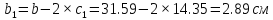
где
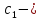 расстояние
от центра тяжести ветви до внутренней
ее грани
расстояние
от центра тяжести ветви до внутренней
ее грани
Принимаем размеры планки:
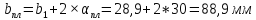 –длина
планки
–длина
планки
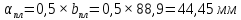 –ширина
планки
–ширина
планки
 –принимаем
толщину планки равную 12мм
–принимаем
толщину планки равную 12мм
Расстояние между планками:
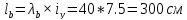
где
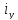 –радиус инерции ветви относительно
оси У
–радиус инерции ветви относительно
оси У
Расстояние между центрами планок:
l=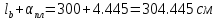
Определяем геометрические характеристики сечения относительно свободной оси У
Момент инерции:
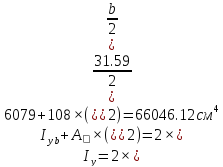
где
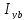 – момент инерции ветви относительно
оси У
– момент инерции ветви относительно
оси У
Радиус инерции:
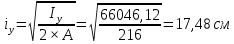
Гибкость:
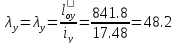
Приведенная гибкость:
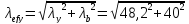 =
62,63
=
62,63
По
приведенной гибкости определяем
коэффициент
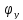 .
.
Условие устойчивости относительно свободной оси У: