Расчет второстепенной балки

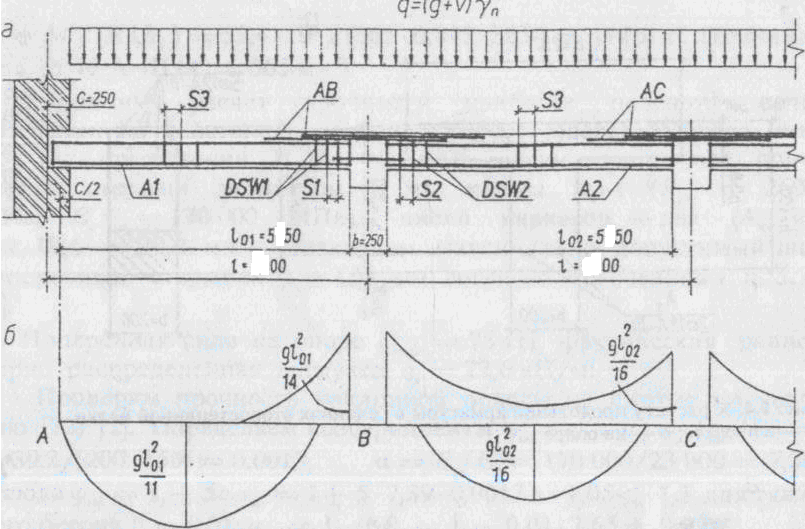
=l-c/2-b/2=5800-250/2-250/2=5550мм=5,65м

Постоянная нагрузка

от собственного веса плиты и пола 3,64*2,4=8,736 кН/м

от веса ребра балки 0,2*(0,4-0,08)*25*1,1=1,76 кН/м

итого: g=10,496 кН/м

Временная нагрузка v=7,2*2,4=17,28 кН/м

Итого с учетом коэффициента по назначению здания:

q=(g+v) γn=(10,496+17,28)*0,95=26,39 кН/м

Изгибающие моменты с учетом перераспределения усилий:

В первом пролете М=/11=26,39*/11=76,58 кН*м

На первой промежуточной опоре М=/14=26,39*/14=60,17кН*м

Максимальная перерезывающая сила на первой промежуточной опоре равна:

Q=0,6*q=0,6*26,39*5,65=89,5 кН

Для арматуры класса А-IIIRs=365МПА

Проверяем правильность предварительного назначения сечения второстепенной балки:

, или

h0+a=282,4+35=317,4<400, увеличивать сечение не требуется.

Расчет сечений, нормальных к продольной оси балки на действие изгибающих моментов

Сечение в пролете(М=76,58 кН*м)

Расчетная ширина полки таврового сечения при

и 2*1/6l0+b=2*1/6*5650+200=2083, поскольку 2083<2250 принимаем=2083мм

Вычислим h0=h-a=400-30=370мм

т.к. Н*м = 527кН*м>76,58 кН*м, т.о. граница сжатой зоны проходит в полке.

Вычисляем:

αm=M/(Rb*b*)=74,74*= 0,0348<αR=0,44, тогда ζ=0,9823, требуемая площадь арматуры равна:

As=M/(Rsζh0)=

Выбираем 2Ø20(Аs=628) A-III

Сечение на первой промежуточной опоре (М=60,17 кН*м)

Вычислим h0=h-a=400-35=365 мм

αm=M/(Rb*b*)=60,17*=0,173<αR=0,422, т.е. сжатая арматура не требуется, тогда при ζ=0,987, определим площадь растянутой арматуры:

As=M/(Rsζh0)=. Выбираем 5 Ø12 A-III (As=565)

Расчет на прочность при действии поперечной силы у опоры

Принимаем поперечные стержни диаметром 5 мм класса Вр-I(Rsw=260 МПа, Еs=170000МПа), число каркасов-2 (Asw= 2*19,6=39,2)

Назначаем шаг стержней s=150мм.

Поперечная сила на опоре Qmax=89,5 кН, фактическая равномерно распределенная нагрузкаq1=26,39

Проверка прочности наклонной полосы на сжатие.

μw=Asw/(b*s)=39,2/(200*150)=0,0013

α=Es/Eb=170000/30000=5,67

φw1=1+5αμw=1+5*0,0013*5,67=1,04

φb1=1-βRb=1-0,01*7,65=0,923

Тогда 0,3* φw1*φb1*Rb*b*=0,3*1,04*0,8695*13,05*200*370=261979H=262,0 кН>Qmax=89,5 кН, т.е. прочность наклонной полосы ребра балки обеспечена.

Проверка прочности наклонного сечения.

Определим величины Мbиqsw:

φb2=2, принимаем, тогда φf==0,75*240*80/(200*370)=0,195<0,5;Mb=φb2*(1+ φf)*Rbt*b*=

2*(1+0,195)*0,675*200*=44,17*Н*мм=44,17кН;

qsw=Rsw*Asw/s=260*39,2/120=84,9 Н/мм(кН/м).

Определим значение Qb,minпринимаяφb3=0,6

Qb,min=φb3*(1+φf)*Rbt*b*=0.6(1+0.195)*0.675*200*370=35,81 кН/м.

Определяем длину проекции опасного сечения С.

Так как 0,56qsw=0,56*84,9=47,544 кН/м>q1=26,39кН/м, значение с определяем по формуле:

С===1,67м

Поскольку С=1,67>( φb2/φb3)* =(2/0,6)*0,37=1,23м, принимаем С=1,23 м

Тогда Qb=Мb/C=73,62/1,23=59,85 кН>59,69 и

Q=Qmax-q1*C=89,5-26,39*1,23=57,04 кН

Длина проекции наклонной трещины будет равна:

С0===0,931

С0=0,931м>2h0=2*0,37=0,74, принимаем С0=0,74, тогдаQsw=qsw*C0=84,9*0,74=62,826кН/м

Проверяем условие Qb+Qsw=59,85+62,826= 122,67кН>57,04кН