Федеральное агентство железнодорожного транспорта

Федеральное государственное образовательное учреждение

высшего профессионального образования

«Петербургский Государственный Университет Путей Сообщения Императора Александра I»

Кафедра «Математика и моделирование»

Контрольная работа по дисциплине

«Методы оптимальных решений»

Выполнил: Студент

учебной группы

14 ЭБС – 230 Евдокимова. Н.Н.

Проверил:

Руководитель

Санкт – Петербург

2016

Вариант контрольной работы №10.

Задание 1.

Для функции двух переменных , заданной следующим выражением:

Задачи, поставленные в задании:

1. Найти стационарную точку и вычислить в ней значение функции;

2. Найти экстремальные точки и экстремальные значения;

3. Найти области выпуклости (вогнутости) функции.

Решение:

1. Для нахождения стационарной точки найдем частные производные, прировняем их к 0, вычислим систему уравнений, так найдем координаты стационарной точки.

= 7*2x₁+2x₂+1; = 2x₁+5*2x₂ – 10;

;;

;;

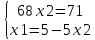Точка M с координатами (-15/68; 71/68) - стационарная точка.

Значение функции двух переменных в точкеM вычислено при помощи Microsoft Excel.

Z (-15/68 ; 71/68) = −10 ;

2. Чтобы найти экстремальные точки и экстремальные значения найдем частные производные второго порядка.

Обозначим:.

A = =14;;= 10

и через ∆ = AC – B² = 14*10 −2² = 136; ∆ ˃ 0;

Так как ∆ ˃ 0, и A ˃ 0 то по достаточному условию экстремума функция Z имеет в точке М (-15/68 ; 71/68) минимум, причем значение функции Z = −10;

3. Так как функция Z дважды дифференцируема и Z’’(x₁;x₂) ˃ 0,

то функция Z – выпуклая.

Ответ:

1. Точка M с координатами (-15/68; 71/68) - стационарная точка.

Значение функции в точке M равно = −10

2. Функция Z имеет в точке М (-15/68 ; 71/68) минимум.

3. Функция Z – выпуклая.

Задание 2.

Функция трех переменных задана следующим выражением.

Задачи, поставленные в задании:

a. Найти стационарную точку функции и вычислить в ней ее значение;

b. Найти экстремальные точки и экстремальные значения функции;

c. Найти области выпуклости (вогнутости) функции.

Решение:

1. Найдем частные производные.

= 6x₁ + 2x₂ – x₃ + 4; 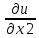= 4x₂ + 2x₁ + 5x₃ – 1; = 10x₃ – x₁ + 5x_2;

Составим и решим систему уравнений для нахождения стационарных точек.

Решив систему уравнений при помощи Microsoft Excel, с помощью обратной матрицы, найдены корни уравнений.

x₁ = -3,27; x₂ = 6,12; x₃ = -3,38

Найдена одна стационарная точка M (-3,27; 6,12; -3,38)

Значение функции U в точке M равно, U = 135,37

2. Чтобы найти экстремальные точки и экстремальные значения найдем частные производные второго порядка.

= 6; =2; = -1;

= 2; = 4; = 5;

= -1; = 5; 10;

Составим матрицу Гессе:

H =

Продолжение решения через анализ угловых миноров матрицы Гессе.

Достаточные условия экстремума. Если в некоторой точке выполнены необходимые условия

экстремума и все частные производные 2-го порядка непрерывны, то существование экстремума в этой точке

определяется значениями угловых миноров матрицы вторых производных (матрицы Гессе):

M1 ˃ 0 , M2 ˃ 0 - локальный минимум;

M1 ˂ 0 , M2 ˃ 0 - локальный максимум;

M2 ˂ 0 - экстремума нет.

Так как угловые миноры : M₁ = 15; M₂ = 10, следовательно на основании достаточного условия экстремума, функция

в точке M (-3,27; 6,12; -3,38) имеет локальный минимум.

3. Достаточным условием выпуклости функции f (x1, x2, …, xn) является положительная определенность матрицы.

Составим главные определители матрицы Гессе.

∆₁ = 15; ∆₂ = 10; ∆₃ = 59;

Так как все определители ˃ 0, то матрица H положительно определена и функция выпуклая.

Ответ:

1. Найдена одна стационарная точка M (-3,27; 6,12; -3,38)

Значение функции

в точке M равно, U = 135,37

2. В точке M (-3,27; 6,12; -3,38) имеет локальный минимум.

3. По критерию Сильвестра, матрица H положительно определена и функция

выпуклая.