
- •1. Особенности условий работы и характеристики электрических цепей автоматики и связи. Электрическая цепь как модель.
- •2. Канонические схемы 2хполюсников rc, свойства их сопротивлений и проводимостей.
- •3. Канонические схемы 2хполюсников rl, свойства их сопротивлений и проводимостей.
- •4. Свойства функций входных сопротивлений и проводимостей пассивных 2хполюсников. Приемы построения 2хполюсных схем по заданным функциям z(p) , y(p).
- •6. Четырехэлементные реактивные 2хполюсники. Примеры использования реактивных 2хполюсников в устройствах ат и связи.
- •7. Электрическая цепь как 4хполюсник. Ур-я 4хполюсника с z-параметрами. Физ. Смысл параметров. Связь между параметрами в случаях симметричности и обратимости. Схемы замещения.
- •8. Ур-я 4хполюсника с y-параметрами. Физ. Смысл параметров. Связь между параметрами в случаях симметричности и обратимости. Схемы замещения.
- •9. Уравнения 4хполюсника с параметрами abcd. Физ. Смысл параметров. Связь между параметрами в случаях симметричности и обратимости. Примеры применения 4хполюсных цепей в устройствах ат и связи.
- •10. Схема замещения 4хполюсника т, ее матрицы параметров z и abcd.
- •11. Схема замещения 4хполюсника п, ее матрицы параметров y и abcd.
- •12. Симметричные схемы замещения т и п и их параметры передачи.
- •13. Последовательное и параллельное соединение 4хполюсников. Определение параметров соединения.
- •14. Цепочечное соединение 4хполюсников. Определение параметров соединения.
- •27. Корректоры группового времени прохождения сигналов (фазовые корректоры). Порядок синтеза схемы корректора с заданными с-вами.
- •28. Цепи с распределенными параметрами. Первичные параметры электрической линии. Решение диф. Ур-й линии для установившегося режима переменного тока.
- •29. Анализ решения диф. Ур-й линии. Волновые процессы в линии (падающие и отраженные волны напряжения и тока в линии, волновые параметры линии).
- •30. Взаимодействие падающих и отраженных волн в линии. Коэффициент отражения.
- •31. Связи между напряжениями и токами на входе и выходе линии (общий случай).
- •32. Особенности волновых процессов в линии без потерь. Связи между напряжениями и токами на входе и выходе линии. Свойства линии длиной λ/ 4.
- •35. Цифровые фильтры (элементная база, виды реализации). Линейная модель цифрового фильтра. Рекурсивные и трансверсальные цифровые фильтры.
- •37. Импульсные хар-ки и передаточные ф-ции трансверсального и рекурсивного(ких и бих) фильтров.
- •38. Задачи синтеза цифровых фильтров. Билинейное преобразование.
13. Последовательное и параллельное соединение 4хполюсников. Определение параметров соединения.
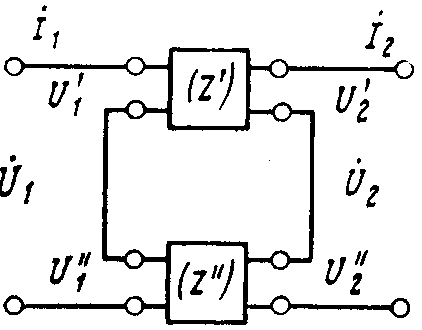
Последовательное соединение характеризуется соотношением:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Для 2х соединенных 4хполюсников:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
Отсюда:
![]()
![]()
Значит
![]() ;
;![]() ;
;
![]() ;
;
![]() .
.
Запишем матрицу сопротивлений:
![]()
![]() =
=![]()
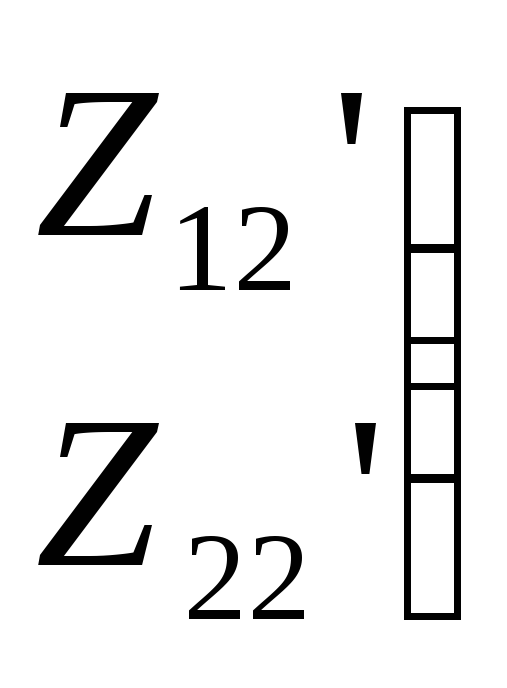 +
+![]()
![]()
Т.о. каждый последовательно соединяемый 4хполюсник следует характеризовать матрицей сопротивлений х.х. и эти матрицы сложить. Число соединяемых 4хполюсников м.б. любым.
Параллельное соединение:
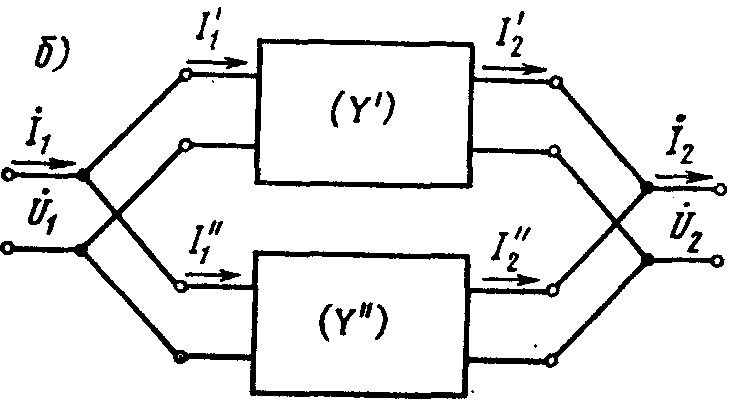
Параллельное соединение характеризуется соотношением:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Для 2х 4хполюсников:
![]()
![]()
![]()
![]()
Отсюда:
![]() ;
;
![]()
Отсюда:
![]()
![]() =
=![]()
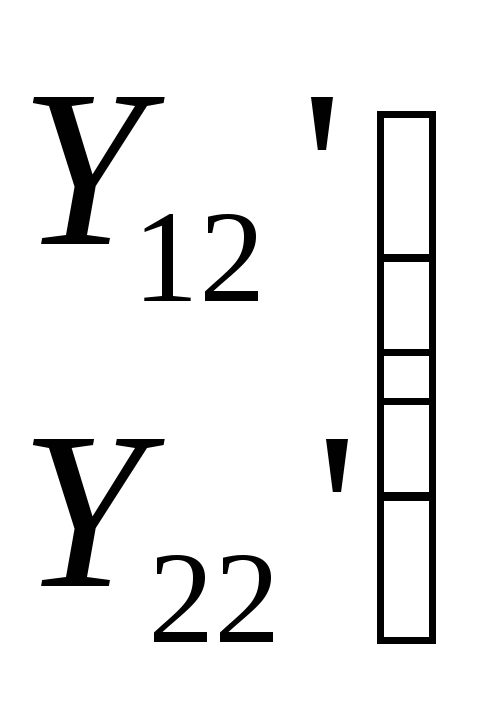 +
+![]()
![]()
Т.о. матрица проводимостей параллельно соединенных 4хполюсников равна сумме матриц проводимостей4хполюсников, входящих в соединение.
14. Цепочечное соединение 4хполюсников. Определение параметров соединения.
![]()
При цепочечном соединении 2х 4хполюсников:
![]() ;
;
![]() ;
;![]() ;
;
![]() ;
;
![]() ;
;![]() .
.
Тогда для определения параметров соединения воспользуемся уравнениями передачи:
![]() ;
;
![]()
![]() ;
;
![]()
Отсюда получим:
![]()
![]()
Группируя члены этих уравнений и убирая штрихи, получим:
![]()
![]()
Полученные ур-я ввязывают напряжение и ток на входе с напряжением и током на выходе.
Если 4хполюсники,
входящие в цепочечное соединение
характеризовать матрицей
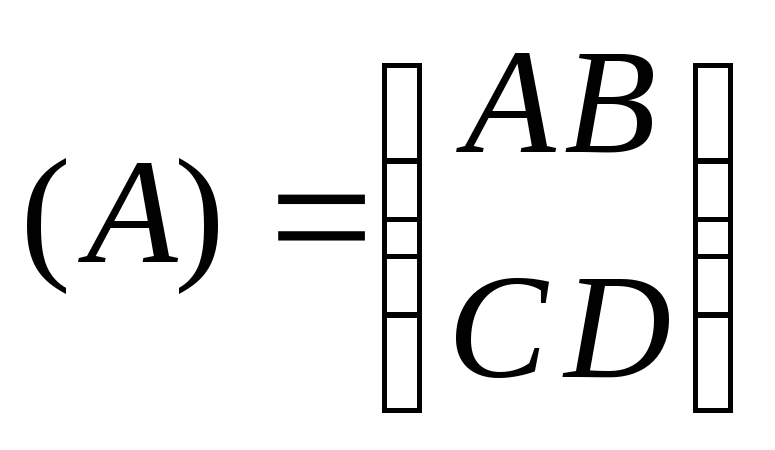 ,
то все соединение можно охарактеризовать
матрицей:
,
то все соединение можно охарактеризовать
матрицей:
![]()
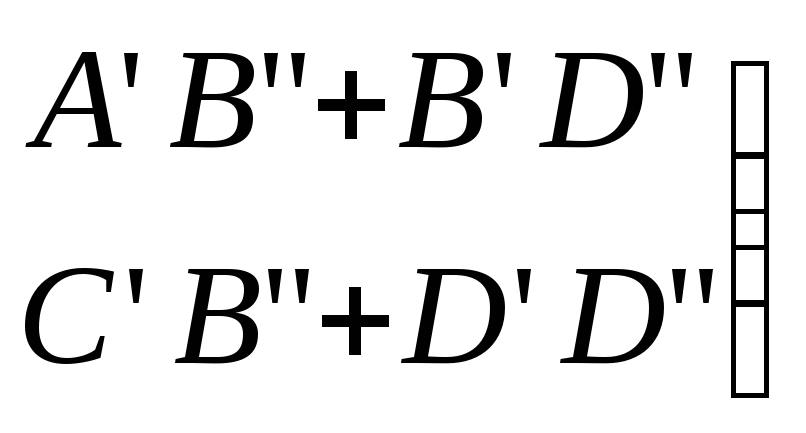
Матрица (А)
цепочечного соединения 4хполюсников
– произведение матриц
![]() и
и![]() 4хполюсников, входящих в это соединение.
4хполюсников, входящих в это соединение.
![]()
![]()
![]()
![]()
27. Корректоры группового времени прохождения сигналов (фазовые корректоры). Порядок синтеза схемы корректора с заданными с-вами.
Если фазовая
скорость
![]() для различных частотных составляющих
неодинакова, то сигнал при передаче
подвергается фазочастотным искажениям.
для различных частотных составляющих
неодинакова, то сигнал при передаче
подвергается фазочастотным искажениям.
![]()
Значение tгр
пр на
определенной частоте
![]() хар-ет время запаздывания огибающей
группы частотных составляющих сигнала,
лежащих в узкой полосе частот вблизи
ω1.
Для цепи с сосредоточенными параметрами
хар-ет время запаздывания огибающей
группы частотных составляющих сигнала,
лежащих в узкой полосе частот вблизи
ω1.
Для цепи с сосредоточенными параметрами
![]()
Для устранения ФЧ
искажений используют корректоры
группового времени прохождения. Фазовые
хар-ки используемых в качестве корректоров
4хполюсников подбирают так, чтобы время
прохождения в откорректированном тракте
с включенным корректором
![]() не зависело от частоты, т.е.
не зависело от частоты, т.е.
![]() -
фазовая хар-ка откорректированного
тракта.
-
фазовая хар-ка откорректированного
тракта.
Мостовая схема с взаимообратными сопротивлениями:
![]() ;
;
![]() ;
;![]()
Независимость ZМ от частоты позволяет хорошо согласовать эти схемы с нагрузками. При реактивных сопр-ях Z1 и Z2:
![]() ;
;
![]()
Значит
![]() ;
;
![]() ;
;
![]() ;
;![]()
Отсюда
![]()
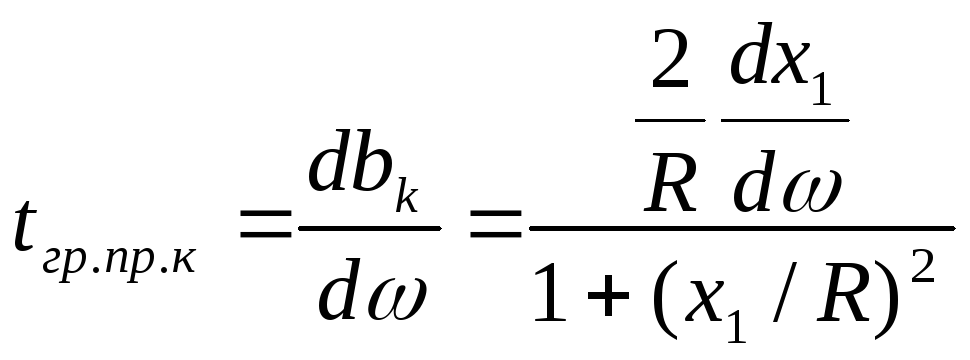
Фазовый контур 1ого порядка:
![]()
![]() ;
;
![]() ;
;![]() ;
;![]()
![]() .
Отсюда
.
Отсюда
![]() ,
гдеk=L/R
,
гдеk=L/R
Функция передачи:
![]()
Фазовый контур 2ого порядка:
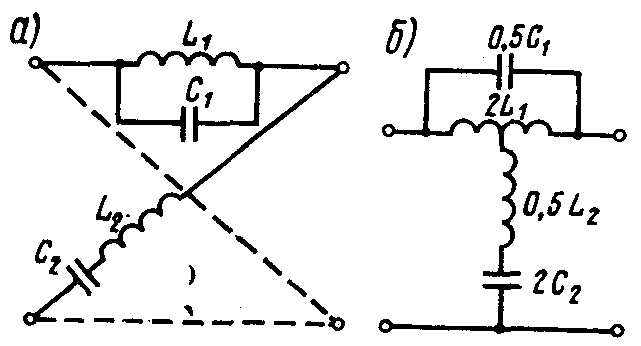
![]() ;
;
![]() ;
;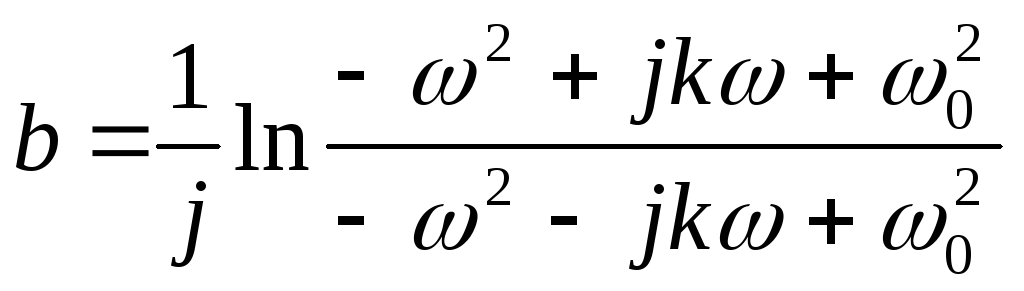
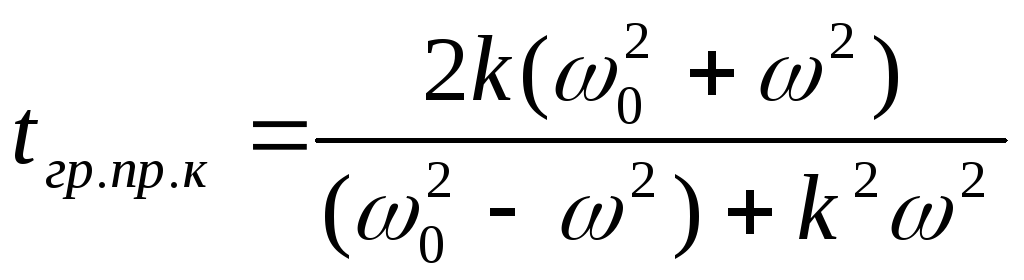
28. Цепи с распределенными параметрами. Первичные параметры электрической линии. Решение диф. Ур-й линии для установившегося режима переменного тока.
При большой длине соединительных проводов, т.е. передаче эл. энергии по линии, длина кот. соизмерима с длиной волны эл/магн. Колебания, нельзя не учитывать сопр-е, индуктивность и емкость, распределенные по всей ее длине. Эл. и магн. Поля в этом случае распределены вдоль линии и пространственно совмещены. Такая линия – эл. цепь с распределенными параметрами.
Для получения исходных соотношений, определяющих процессы в цепях с сосредоточенными параметрами, используют первичные параметры: сопр-е проводов R (Ом/км), их индуктивность L (Гн/км), проводимость изоляции G (1/Ом·км), емкость проводов С (Ф/км).
![]()
![]()
Это диф. ур-я линии.
Продиф-ем 1ое Ур-е по х:
![]() =>
=>
![]()
Обозначим
![]() ,
тогда:
,
тогда:
![]() ,
γ – коэффициент распространения волны
,
γ – коэффициент распространения волны
Отсюда
![]()
Соответственно для тока:
![]() =>
=>
![]()
![]()
Причем
![]() ,
гдеZB
– волновое сопр-е линии.
,
гдеZB
– волновое сопр-е линии.
Решение системы диф. ур-й:
![]()
![]()
Где
![]()
Величины γ и ZB – вторичные параметры линии.
