9. Уравнения 4хполюсника с параметрами abcd. Физ. Смысл параметров. Связь между параметрами в случаях симметричности и обратимости. Примеры применения 4хполюсных цепей в устройствах ат и связи.
Пусть рассматриваемая 4хполюсная цепь представляет собой промежуточное звено в какой-то системе передачи эл. энергии и имеет вход (зажимы 1) и выход (зажимы 2).
В данном случае наиболее удобны ур-я 4хполюсника, решенные относительно U1 и I1.
;
Принято обозначать:
,
,
,
.
Тогда:
;
Где
-
величина, обратная коэффициенту
трансформации по напряжению при
разомкнутых зажимах 2;
–
величина, обратнаяY21
– проводимости передачи при замкнутых
зажимах 2;
–
величина, обратнаяZ21
– сопротивлению передачи при разомкнутых
зажимах 2 ;
-
величина, обратная, коэф-ту трансформации
по току при закороченных зажимах 2.
При разомкнутых
зажимах 2 (х.х.) ток I2=0
и
;
При к.з. зажимов 2
напряжение U2=0
и
;
Свойство обратимости: AD–BC=1
Для обратимого 4хполюсника коэффициенты A, B, C, D Ур-я обратной передачи:
;
Если не учитывать знак «–», появившийся из-за выбора направления тока противоположным направлению передачи, то:
;
Если 4хполюсник симметричен, то A=D, т.к. условия передачи энергии не должны зависеть от ее направления.
Теорию 4хполюсника используют для создания электрических цепей с определенными передающими свойствами, которые задают в виде частотных зависимостей параметров, связывающих напряжение и токи, а по параметрам выбирают схему замещения, по которой строят синтезирующую цепь.
10. Схема замещения 4хполюсника т, ее матрицы параметров z и abcd.
Составим для данной схемы ур-я 4хполюсников:
;
Рассмотрим в отдельности режимы х.х. и к.з.
При х.х. (зажимы 3 и 4 разомкнуты):
Ток в сопротивлениях
Z1
и Z2
одинаковый, значит
При к.з. (3 и 4 замкнуты накоротко):
Полные напряжения и ток на входе:
;
Это и есть ур-е схемы замещения Т.
Между коэффициентами A, B, C, D вып-ся соотношение AD-BC=1.
Ур-я схемы Т так же можно представить в виде:
Отсюда найдем:
;
Матрица параметров ABCD:
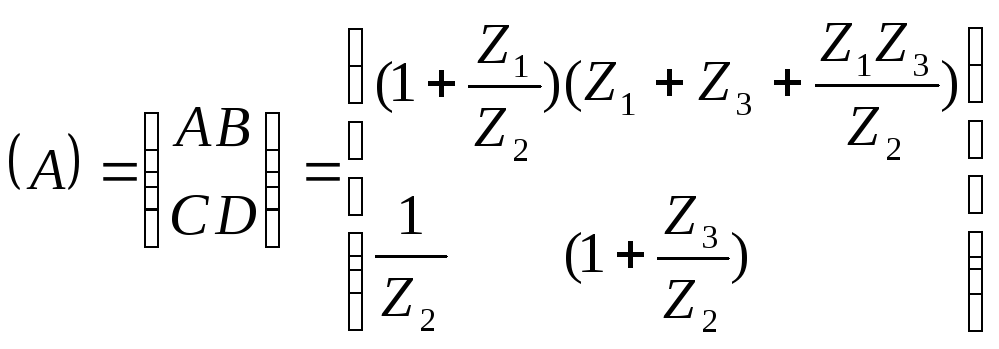
Матрица параметров Z – матрица сопротивлений х.х.:
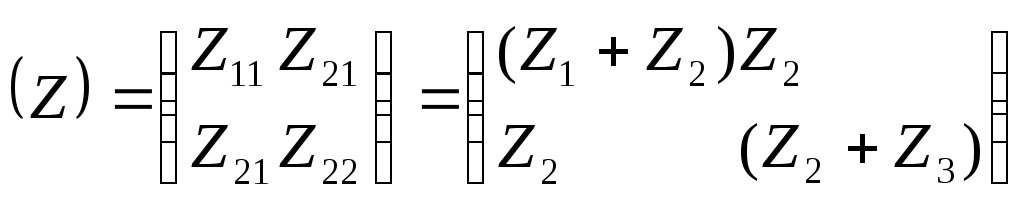
11. Схема замещения 4хполюсника п, ее матрицы параметров y и abcd.
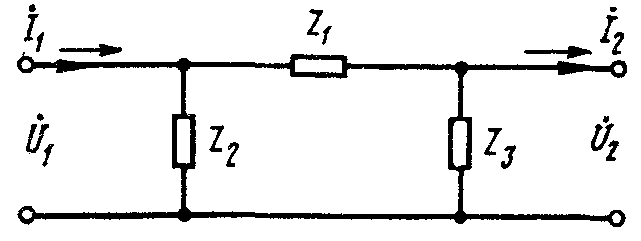
Рассмотрим режимы х.х. и к.з. При х.х. напряжение на входе равно сумме напряжения U2 и падения напряжения на Z1.
Ток на входе равен сумме токов в сопротивлениях Z2 и Z3.
При к.з.
;
Полные напряжение и ток на входе:
;
Матрица параметров ABCD:
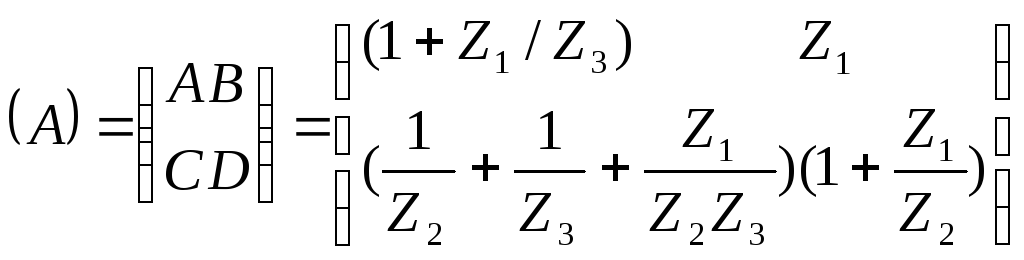
Между коэффициентами A, B, C, D вып-ся соотношение AD-BC=1.
Ур-я схемы П также можно представить в виде:
Матрица параметров Y – матрица проводимостей к.з.:
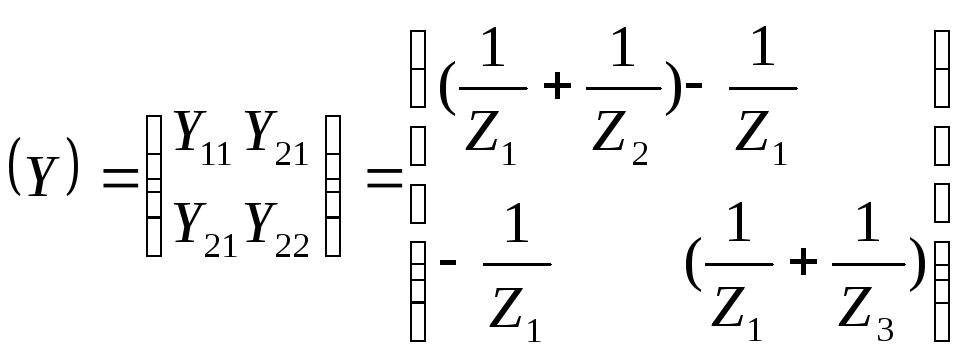
12. Симметричные схемы замещения т и п и их параметры передачи.
Каждую из схем можно представить, как составленную из 2х частей, называемых схемами Г:
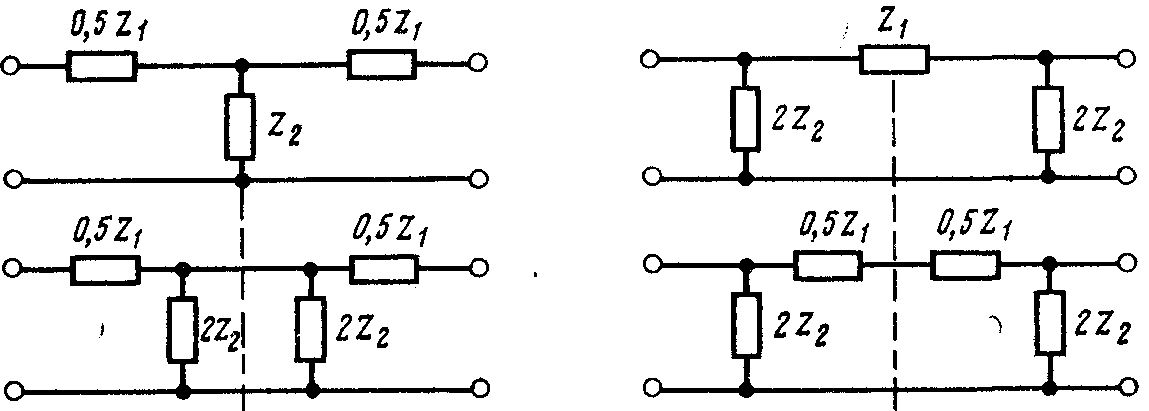
Для схемы Г:
Отсюда
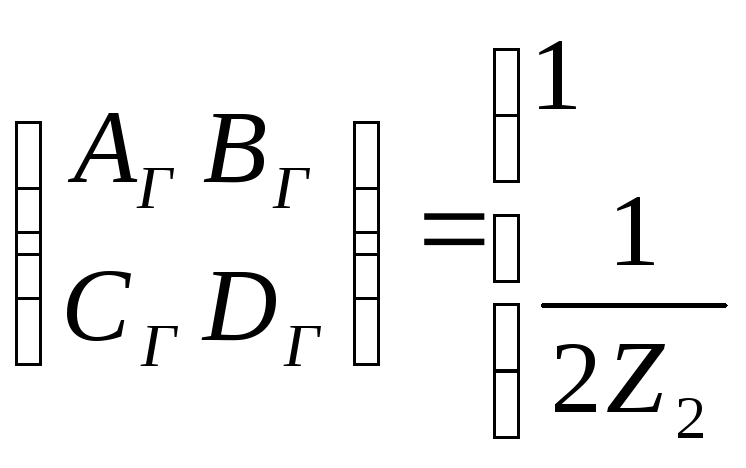
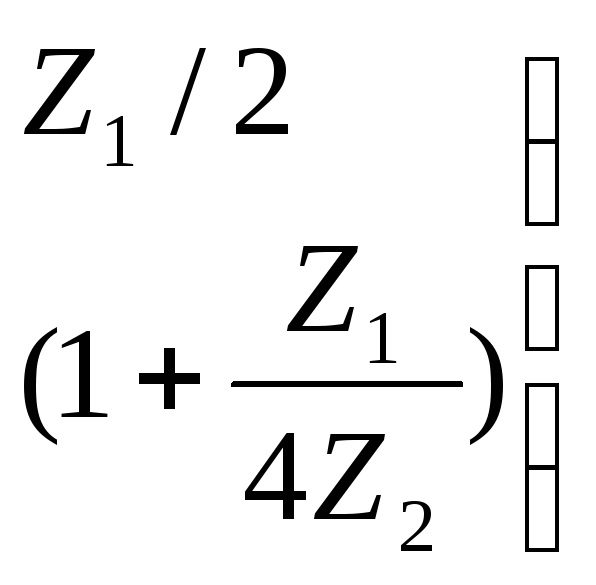
Ур-я симметричных схем для схемы Т:
Ур-я симметричных схем для схемы П:
Матрицы параметров ABCD для схемы Т:
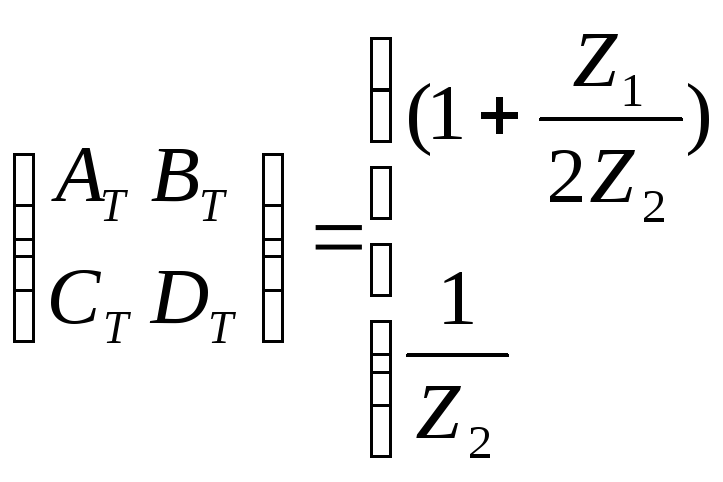
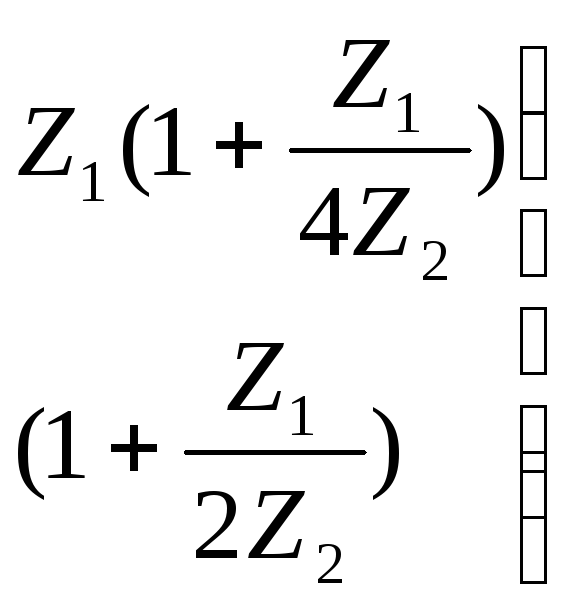
Матрицы параметров ABCD для схемы П:
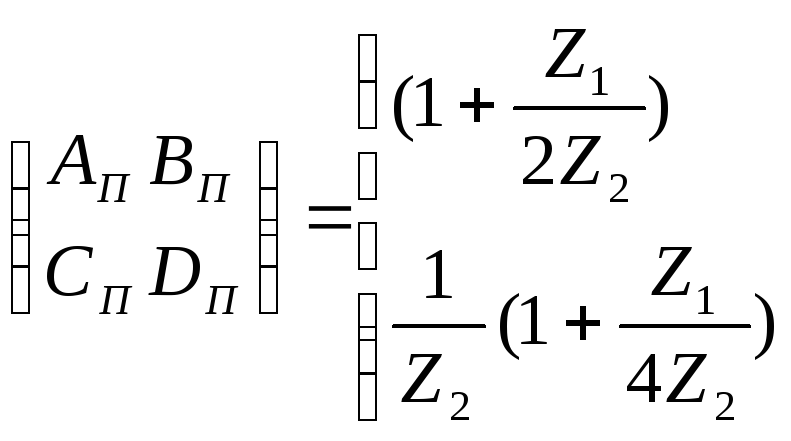
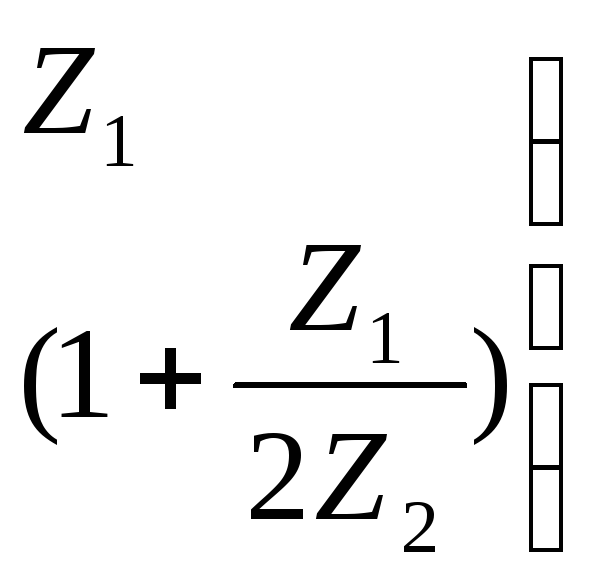
Для всякого
симметричного 4хполюсника A=D.
При этом для обратимых 4холюсников
