6. Четырехэлементные реактивные 2хполюсники. Примеры использования реактивных 2хполюсников в устройствах ат и связи.

Вариантов схем 4хэлементных 2хполюсников может быть 8.

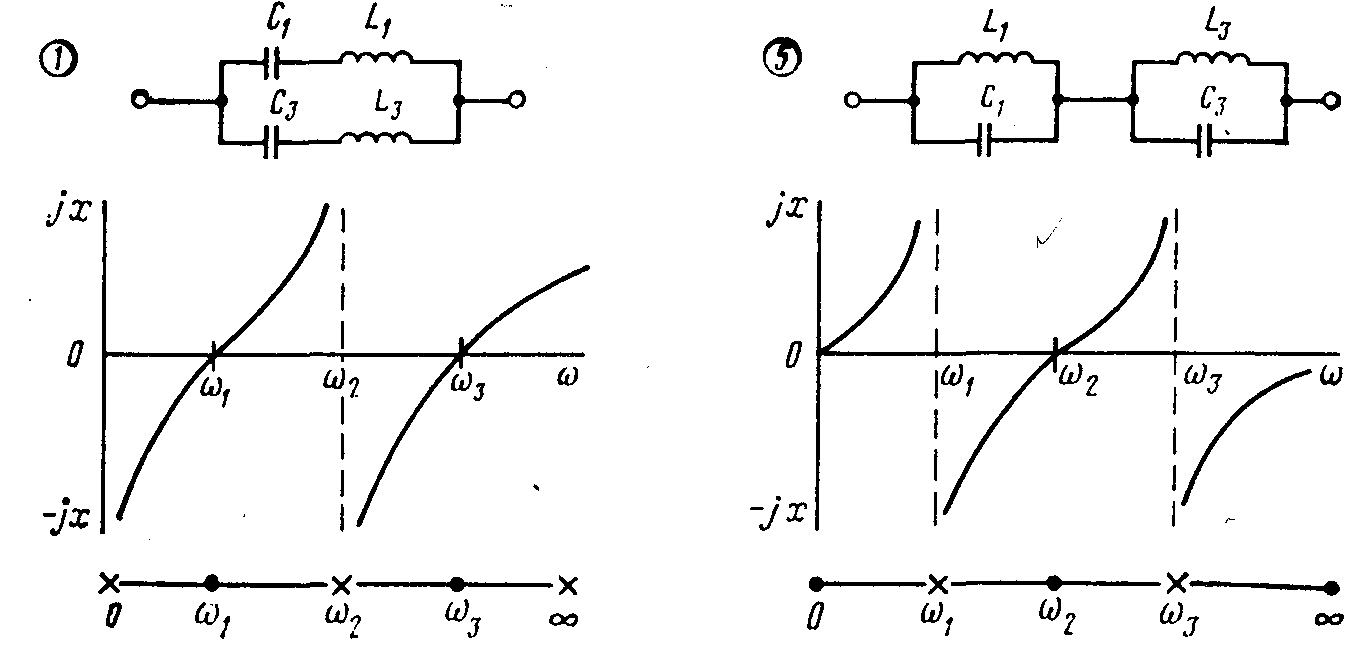
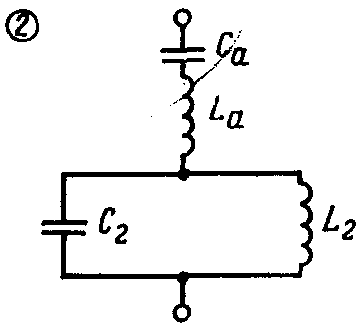
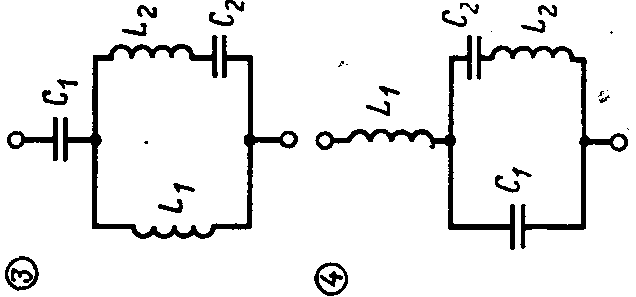
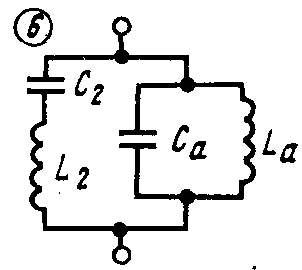
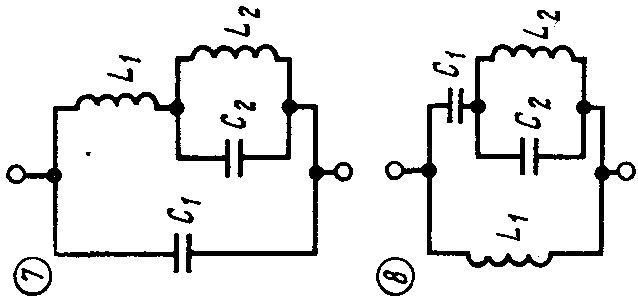
2хполюсник, не пропускающий постоянный ток содержит 2 резонанса напряжений и 1 резонанс токов на конечных угловых частотах. Т.о. общее выр-е сопр-я имеет вид:

Для схемы 1 проводимость 2хполюсника:

Для 2хполюсника 2:

Для 2хполюсника 3:

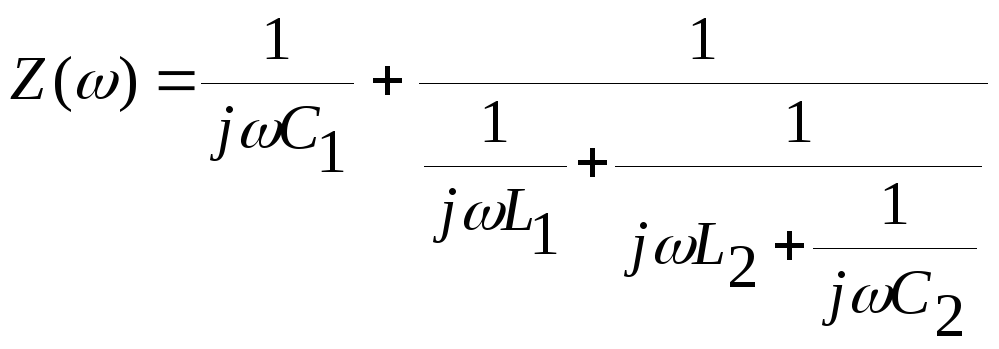
Для 2хполюсника 4:

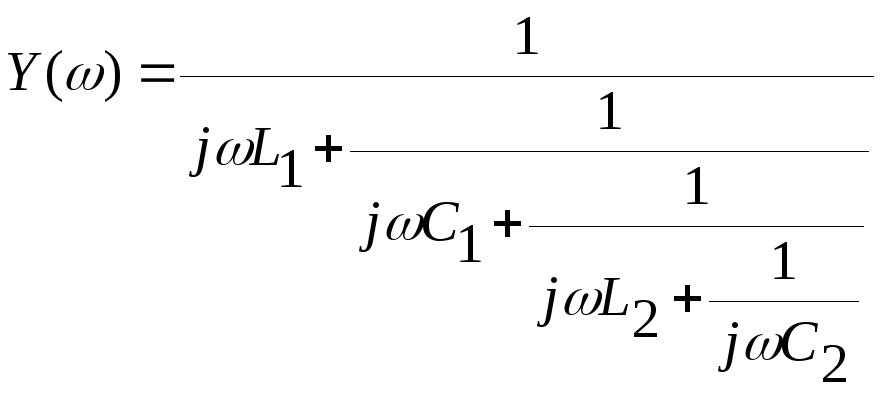
Общее выр-е для сопр-я 2хполюсников, пропускающих пост. ток:

Для схемы 2хполюсника 5:

Для 2хполюсника 6:

Для 2хполюсника 7:

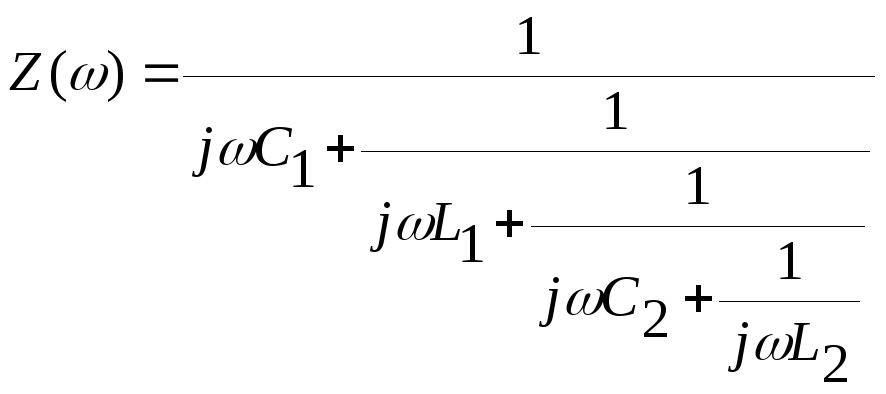
Для 2хполюсника 8:

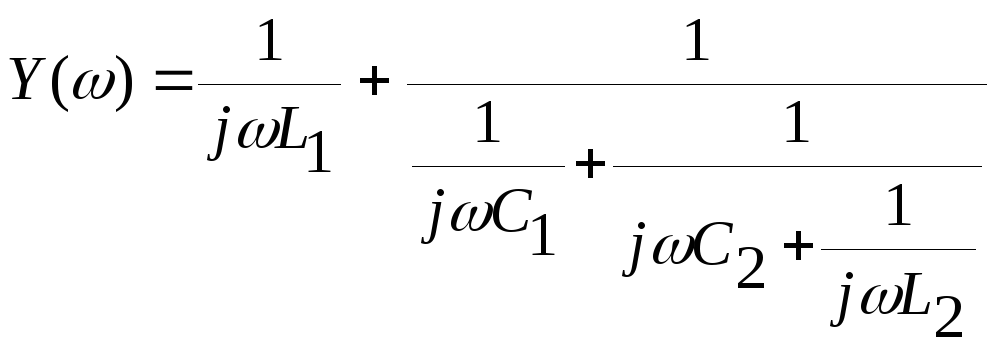
7. Электрическая цепь как 4хполюсник. Ур-я 4хполюсника с z-параметрами. Физ. Смысл параметров. Связь между параметрами в случаях симметричности и обратимости. Схемы замещения.

4хполюсная цепь с 2мя входами (или входом и выходом)хар-ся связями между напряжениями U₁, U₂ и токами I₁, I₂.

Эти связи можно представить по-разному в зависимости от того, какие 2е из величин заданы. Ур-я с параметрами Z: Пусть заданы токи I₁, I₂, надо найти U₁, U₂. Если схема разветвленной цепи, рассматриваемой как 4хполюсник, известна, для нее можно составить с-му ур-й узловых напряжений: ;.

Δ – определитель матрицы проводимости к.з. цепи

Δ₁₁ и Δ₁₂ – его алгебраические дополнения.

Коэффициенты при токах – сопротивления, поэтому:

; .

Z₁₁ – вх. сопр. 4хполюсника, измеренное со стороны входа 1 при разомкнутом входе 2; Z₂₂ – вх. сопр. 4хполюсника, измеренное со стороны входа 2 при разомкнутом входе 1; Z₁₂, Z₂₁ – сопр. передачи, измеренные при размыкании обоих входов.

Данные ур-я наз-ют уравнениями 4хполюсника. Все вместе сопр-я Z_ij – сопротивления (параметры) холостого хода 4хполюсника.

Представленная 4хполюсником цепь, содержащая только пассивные элементы, обладает свойством обратимости. В этом случае Z₁₂=Z₂₁, а 4хполюсник называют обратимым (взаимным).

Схему двухконтурной цепи, соответствующую ур-ям обратимого 4хполюсника, называют схемой замещения Т-обратимого 4хполюсника.

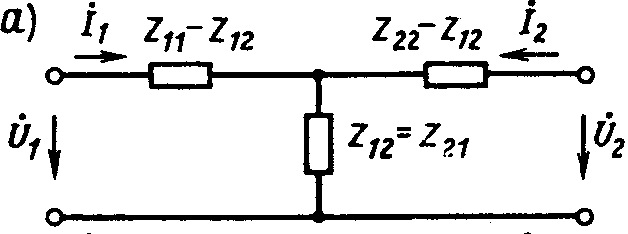Она содержит три сопр-я, кот.

однозначно определяются 3мя

независимыми параметрами

4хполюсника.

4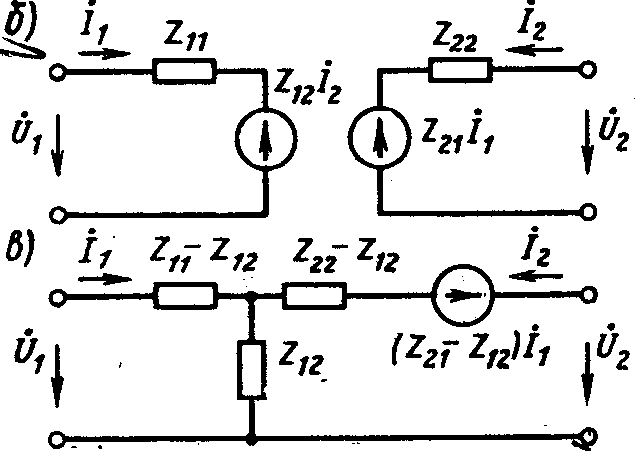хполюсних называютсимметричным, если равны его вх. сопр-я Z₁₁=Z₂₂. У симметричного обратимого 4хполюсника независимы только 2 параметра, остальные определяются из Z₁₂=Z₂₁ и Z₁₁=Z₂₂. Схема замещения 4хполюсника:

Ур-я 4хполюсника в матричной форме:

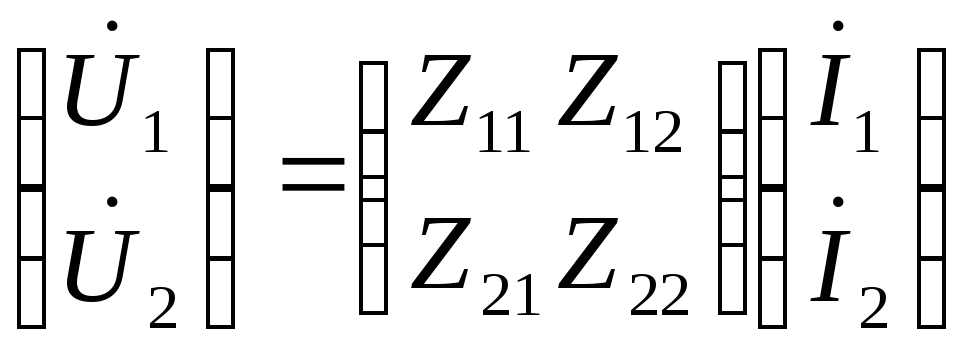или

Матрицу (Z) называют матрицей сопротивлений х.х. 4хполюсника.

8. Ур-я 4хполюсника с y-параметрами. Физ. Смысл параметров. Связь между параметрами в случаях симметричности и обратимости. Схемы замещения.

Ур-я 4хполюсника;можно решить относительно токовI₁ и I₂:

;

Обозначим,,,. Тогда:

; (1), гдеY₁₁ – вх. проводимость 4хполюсника, измеренная на входе при закороченном выходе; Y₂₂ – вх. проводимость, измеренная на выходе при закороченном входе; Y₁₂, Y₂₁ – проводимость передачи, измеренная при закороченных входах.

Д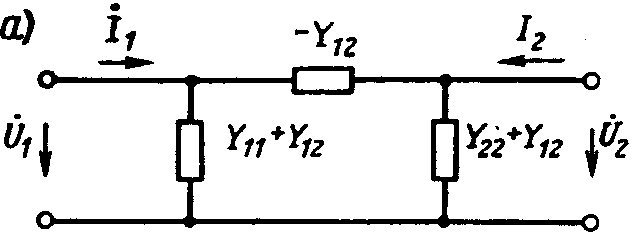ля обратимого 4хполюсникаY₁₂=Y₂₁. Схема замещения П-обратимого 4хполюсника:

У обратимого симметричного 4хполюсниканезависимы 2 параметра: входная проводимость и проводимость передачи, остальные определяем из уравнений: Y₁₂=Y₂₁ и Y₁₁=Y₂₂. Варианты 2хузловых схем, соответствующих ур-ям (1), с зависимыми источниками тока:

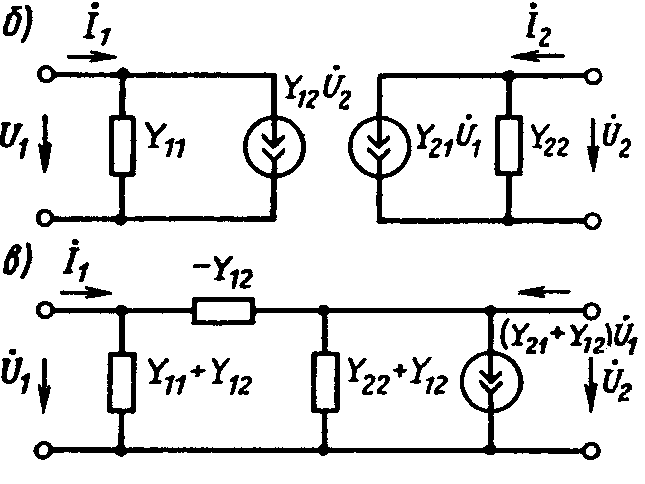
Уравнения (1) в матричной форме:

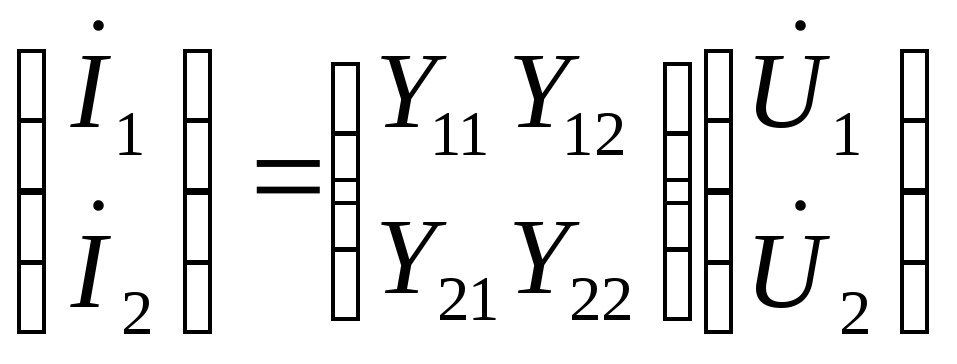или

Матрицу (Y) называют матрицей проводимостей короткого замыкания 4хполюсника.