7. Отражение экстремалей Краткие теоретические сведения

Рассмотрим задачу вариационного исчисления для функционала (1.1), зависящего от функции одной переменной и её производной. Пусть для этого функционала заданы граничные условия (1.2) и дополнительное требование: экстремальy(x) касается заданной кривойy(x) в неизвестной точкеM₀(x₀,y₀), гдеx₀[x₁,x₂] (рис.7.1). В точкеM₀(x₀,y₀) экстремаль не обязательно должна быть гладкой.

Рис. 7.10. Отражение экстремалей

Выведем необходимые условия экстремума для этой вариационной задачи. Так как функционал J(y) достигает экстремума на интервале [x₁,x₂], то он достигает также экстремума и на интервалах [x₁,x₀]и [x₀,x₂]. Следовательно, на каждом из этих интервалов экстремаль должна удовлетворять дифференциальному уравнению Эйлера (1.5).Решения этого уравнения на левом y^l(x) и на правоминтервалах y^r(x) содержат по 2 произвольные постоянные:C₁^l,C₂^lиC₁^r,C₂^r. Кроме того, неизвестны также 2 координаты точки касанияx₀,y₀. Для опредения этих 6 неизвестных мы имеем уравнения:

1. граничное условие на левом конце y^l(x₁)y₁;

2. граничное условие на правом конце y^r(x₂)y₂;

3. y^l(x) проходит через точкуM₀:y^l(x₀)y₀;

4. y^r(x) также проходит черезM₀:y^l(x₀)y₀;

5. точка M₀лежит на линииy(x):y₀(x₀).

Недостающее 6-е уравнение получим из необходимого условия экстремума функционала: J0. Вариация функционала на каждом из двух участковJ₁иJ₂вызывается вариацией функцииy(x) (вместе с её производнойy(x)) и вариацией точкиx₀. В главе 6 было выведено условие трансверсальности (6.7) для функционала с подвижной правой границей. В нашей задаче этоJ₁:

. (7.0)

Аналогично

. (7.0)

Приравнивая сумму этих вариаций нулю и учитывая, что x₀– произвольная, получим недостающее 6-е уравнение:

. (7.0)

Это условие является условием трансверсальности для задачи отражения. Его смысл следующий: если точку x₀двигать по линииy(x)и находить паруэкстремалей (решений уравнения Эйлера)y^l(x) иy^r(x), удовлетворяющих граничным условиям, то доставлять экстремум функционалу будет та пара функций, которая удовлетворяет условию трансверсальности (7.3).

Задача для самостоятельного решения.Выведите условия трансвер­сальности для задачи отражения функционала (2.1), зависящего от двух функций. Рассмотрите случаи, когда экстремаль отражается от заданной поверхности (вариант 1) и от заданной линии (вариант 2).

Пример выполнения заданий

Найти экстремаль функционала, рассмотренного ранее в примере 1a, при тех же граничных условиях, и при дополнительном требовании: экстремаль касается заданной линии в точке M₀(x₀,y₀). Сравнить решение с 1a.

(7.0)

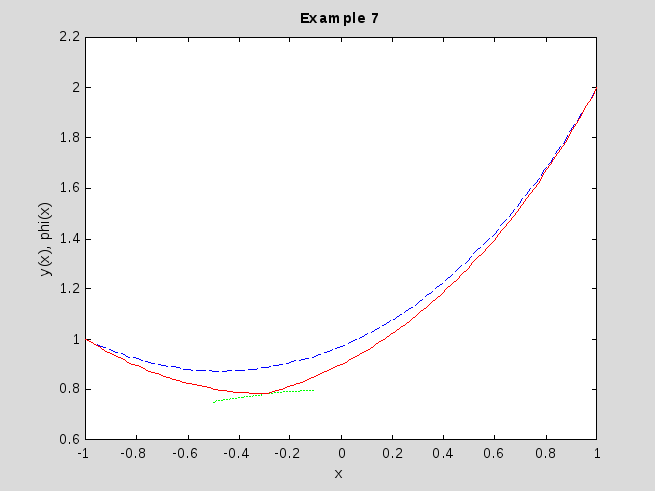
Рис. 7.11. Решение примера 7

Ответ.Экстремаль функционала (7.4) имеет вид

(7.0)

График экстремали показан на рис.7.2 сплошной красной линией. Штриховая синяя линия – решение примера 1a, зелёным цветом показан участок линии, которой касается экстремаль.

Задание

Для функционала 1aнайти экстремаль при дополнительном условии, что эта экстремаль касается заданной линии.

Варианты заданий

Вариант 1. Вариант 2.

Вариант 3. Вариант 4.

Вариант 5. Вариант 6.

Вариант 7. Вариант 8.

Вариант 9. Вариант 10.

Вариант 11. Вариант 12.

Вариант 13. Вариант 14.

Вариант 15. Вариант 16.

Вариант 17. Вариант 18.

Вариант 19. Вариант 20.

Вариант 21. Вариант 22.

Вариант 23. Вариант 24.

Вариант 25. Вариант 26.

Вариант 27. Вариант 28.

Вариант 29. Вариант 30.

8. Преломление экстремалей

Краткие теоретические сведения

Пусть кривая y(x) разделяет плоскостьxOyна две области, и точкиM₁(x₁,y₁) иM₂(x₂,y₂) расположены по разные стороны от этой кривой (рис.8.1).

Рис. 8.12. Преломление экстремалей

Рассмотрим задачу вариационного исчисления для функционала

. (8.0)

Он отличается от функционала, рассмотренного в главе 7 тем, что в нём подынтегральные функции слева и справа от точки M₀(x₀,y₀) – разные. Для вывода необходимого условия экстремума этого функционала воспользуемся результатами главы 7. Каждая из кривых y^l(x),y^r(x) является решением уравнения Эйлера для своей функцииFи содержит по 2 произвольные постоянные:C₁^l,C₂^lиC₁^r,C₂^r. Для нахождения этих 4-х констант и 2-х координат точки преломленияM₀(x₀,y₀) у нас есть уравнения:

6. граничное условие на левом конце y^l(x₁)y₁;

7. граничное условие на правом конце y^r(x₂)y₂;

8. y^l(x) проходит через точкуM₀:y^l(x₀)y₀;

9. y^r(x) также проходит черезM₀:y^l(x₀)y₀;

10. точка M₀лежит на линииy(x):y₀(x₀).

Недостающее 6-е уравнение получим из необходимого условия экстремума функционала:J0. Оно отличается от (7.3) тем, что в левую и правую части равенства входят разные функцииF:

. (8.0)

Уравнение (8.2) является условием трансверсальности для задачи преломления. Его смысл: если точкуx₀двигать по линииy(x)и находить паруэкстремалей (решений уравнения Эйлера)y^l(x) иy^r(x), удовлетворяющих граничным условиям, то доставлять экстремум функционалу будет та пара функций, которая удовлетворяет условию трансверсальности (8.2).

Задача для самостоятельного решения.Выведите условие трансверсальности для задачи преломления функционала (2.1), зависящего от двух функций, когда экстремаль преломляется на заданной поверхности.