Примеры выполнения заданий Пример 5a

Найти экстремаль функционала (1.6), рассмотренного ранее в примере1a, при том же самом граничном условии на левом конце, и при незаданном граничном условии на правом конце. Сравнить решение с решением задачи 1a.

Рис. 5.1. Решение примера 5a

Ответ.Естественное граничное условие на правом конце имеет вид

. (5.0)

После подстановки произвольных постоянных экстремаль

. (5.0)

График её приведен на рис.5.1 сплошной красной линией. Пунктирная синяя линия – решение примера 1a.

Пример 5b

Найти экстремаль функционала (2.4), рассмотренного ранее в примере 2, при тех же самых граничных условиях на левом конце, и при незаданных граничных условиях на правом конце.Сравнить решение с решением примера 2.

Рис. 5.2. Решение примера 5b – функция y(x)

Затем на новом рисунке строим двумерные графики функций z(x), также сплошной красной линией для примера5bи пунктирной синей – для примера2.

Рис. 5.3. Решение примера 5b – функция z(x)

И, наконец, строим трёхмерный график: сплошная красная линия – решение примера5b, а пунктирная синяя – примера2. Выбираем точку просмотра. Показываем сетку и контур.

Рис. 5.4. Решение примера 5b в виде пространственной кривой

Ответ.Естественные граничные условия имеют вид

(5.0)

После подстановки произвольных постоянных уравнения экстремали

(5.0)

На рис.5.2–5.4 показаны соответственно функции y(x), z(x), и графики пространственных кривых.

Задание

Для своего варианта заданий 1aи2найти экстремали, если граничные условия на правом конце не заданы. Сравнить полученные решения с решениями примеров1aи2.

6. Условие трансверсальности Краткие теоретические сведения

Рассмотрим задачу вариационного исчисления для функционала (1.1). Пусть на левом конце задано граничное условие:y(x₁)y₁; а на правом концеx₂график функции проходит через точкуM₂(x₂,y₂), лежащую на заданной линииy(x) (рис.6.1):

Рис. 6.5. Вариационная задача с подвижным правым концом

Выведем необходимое условие экстремума для такого функционала. Так как J(y) достигает экстремума на классе функций с варьируемой правой точкойM₂(x₂,y₂), то он тем более будет достигать экстремума на более узком классе функций – с неподвижной правой точкой. Следовательно, экстремаль должна удовлетворять уравнению Эйлера (1.5). Решение этого уравнения содержит 2 произвольные постоянныеC₁ и C₂, которые нужно определить. Неизвестны также 2 координаты точки сопряженияM₂(x₂,y₂). Для нахождения этих 4-х неизвестных у нас есть условия:

1. граничное условие на левом конце: y(x₁)y₁;

2. экстремаль проходит через неизвестную точку M₂(x₂,y₂):y(x₂)y₂;

3. точка M₂(x₂,y₂) лежит на линии – ограничении:y₂(x₂).

Недостающее четвёртое уравнение выведем из необходимого условия экстремума J0. Вариация функционала вызывается вариацией функцииy(x) (вместе с её производнойy(x))и вариацией правой точкиx₂:

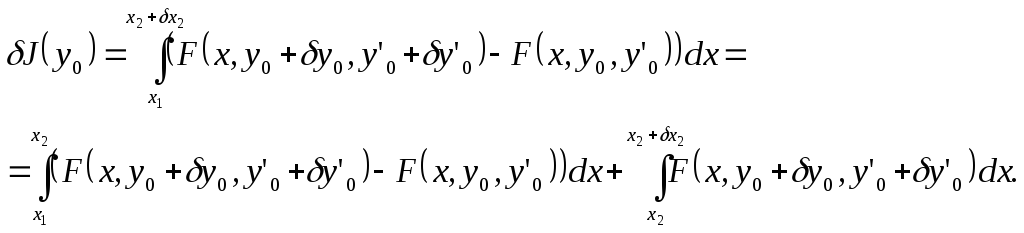(6.0)

Первое слагаемое мы нашли в главе 5 – смотри (5.1):

. (6.0)

Второй интеграл вычисляется на малом участке, поэтому воспользуемся теоремой о среднем. В силу непрерывности подынтегральной функции с точностью до бесконечно малых высшего порядка этот интеграл равен

. (6.0)

Таким образом, необходимое условие экстремума имеет вид

. (6.0)

Из рис.6.2видно, что величинасвязана сy₂соотношением

. (6.0)

Рис. 6.6. Связь между и y₂

Учитывая, что y₂ (x₂)x₂, запишем необходимое условие экстремума:

. (6.0)

В силу произвольности x₂получаем недостающее 4-е уравнение:

. (6.0)

Оно называется условием трансверсальности. Смысл его такой: если двигать точку M₂(x₂,y₂) по линииy(x), и по полученным двум точкам строить экстремали, то из всех экстремалей доставлять экстремум функционалу будет та, которая удовлетворяет условию трансверсальности (6.7).

Таким образом, для решения данной вариационной задачи нужно решить дифференциальное уравнение Эйлера, а затем найти произвольные постоянные C₁,C₂и координаты точкиM₂(x₂,y₂) из решения системы 4-х нелинейных уравнений

(6.0)

Рассмотрим теперь функционал (2.1), зависящий от двух функций y(x),z(x).

.(6.0)

Пусть для него задано только граничное условие при xx₁, а приxx₂экстремаль (пространственная линия) проходит через точкуM₂(x₂,y₂,z₂), лежащую на заданной поверхности или линии.

И в этом случае, если какая-либо кривая доставляет экстремум функционалу на классе функций с подвижной правой точкой, то она тем более будет доставлять ему экстремум на более узком классе функций: с неподвижной правой точкой. Следо­вательно, экстремаль должна удовлетворять системе уравнений Эйлера (2.3). Однако граничных условий для нахождения всех 4-х произвольных постоянных недостаточ­но. Недостающие уравнения получим из необходимого условия экстремума: J0.

(6.0)

В первом слагаемом разложим функцию Fв ряд Тейлора в окрестности экстремали, удержим только линейные члены, и проинтегрируем по частям. Так как искомые функции удовлетворяют системе уравнений Эйлера и граничному условию на левом конце, то первое слагаемое будет:

(6.0)

Для второго слагаемого используем теорему о среднем:

. (6.0)

Необходимое условие экстремума функционала (6.9) имеет вид

. (6.0)

Учитывая, что соотношение (6.5) имеет место и для функции z(x):

, (6.0)

запишем результат

. (6.0)

Отсюда можно вывести условия трансверсальности для различных случаев граничных условий на правом конце.

Пусть, например, правая точка M₂(x₂,y₂,z₂) лежит на заданной поверхностиz(x,y). В этом случае в выражении (6.15)x₂иy₂независимые, аz₂находится дифференцированием уравнения поверхности:z₂_x(x₂,y₂)x₂_y(x₂,y₂)y₂. Подставим эти выражения в (6.15), и приравняем нулю коэффициенты при независимыхx₂иy₂. Получаем условия трансверсальности для этого случая:

(6.0)

Для нахождения 4-х произвольных постоянных и 3-х координат точки M₂ мы имеем систему 7-ми нелинейных уравнений:

• 2 граничных условия на левом конце;

• 2 граничных условия на неизвестном правом конце;

• точка M₂находится на поверхностиz(x,y);

• 2 условия трансверсальности (6.16).

Пусть теперь правая точка M₂(x₂,y₂,z₂) находится на заданной линии

(6.0)

В этом случае в (6.15) независимым будет только x₂, а y₂ и z₂ находятся дифференцированием уравнений (6.17): y₂(x₂)x₂; z₂(x₂)x₂. Подставим эти выражения в (6.15). Приравнивая нулю коэффициент при независимой x₂, получим условие трансверсальности для данного вида граничных условий на правом конце:

. (6.0)

Для нахождения 4-х произвольных постоянных и 3-х координат точки M₂ мы в этом случае будем иметь такую систему 7-ми нелинейных уравнений:

• 2 граничных условия на левом конце;

• 2 граничных условия на неизвестном правом конце;

• точка M₂находится на линии (6.15) (2 уравнения);

• условие трансверсальности (6.18).

Задача для самостоятельного решения.Выведите условие трансверсальнос­ти для функционала (3.1), зависящего от функции и её производных 1-го и 2-го поряд­ка, когда граничные условия (3.2) заданы только на левом конце интервалаx₁, а пра­вый конец движется по заданной линииy(x), причём уголмежду экстремалью и кривойy(x) в точке сопряженияx₂задан (вариант 1) или произвольный (вариант 2).