Задание

Решить примеры 1a,2и3методом начальных параметров. Сравнить решения с аналитическими.

2. Численные методы 2. Метод конечных разностей

3. Краткие теоретические сведения

В методе конечных разностей (МКР) экстремаль аппроксимируется кусочно-линейной функцией. Варьируются ординаты y(x) в заданных точках, и функционал становится функцией этих неизвестных ординатy₁,y₂, ….

Рассмотрим применение МКР к вариационной задаче для функционала (1.1, 1.2). Разобьём интервал [x₁,x₂]на n участков одинаковой длины x(x₂x₁)/n. Будем обозначать точки деления x_k. То есть граничные точки в этом примере в дальнейшем будем обозначать x₀иx_n. Функционал Jбудет равен сумме функционалов на отдельных участкахJ_k. Так как участки малые, применим для вычисления интегралов формулу касательных: каждый изJ_kравен подынтегральной функции, вычисленной в средней точке, и умноженной на ширину интервала:

.(12.0)

Функционал (1.1) будет функцией неизвестных ординат y₁,y₂, …,y_n-1:

.(12.0)

Значения y₀иy_nизвестны – это заданные граничные условия. Для нахождения экстремума продифференцируемJпо переменнымy₁,y₂, …,y_n-1, приравняем производные нулю и решим полученную систему уравнений. При вычисленииJ/y_k учтём, что отy_kзависят только 2 слагаемых формулы (12.2):J_kиJ_k+1.

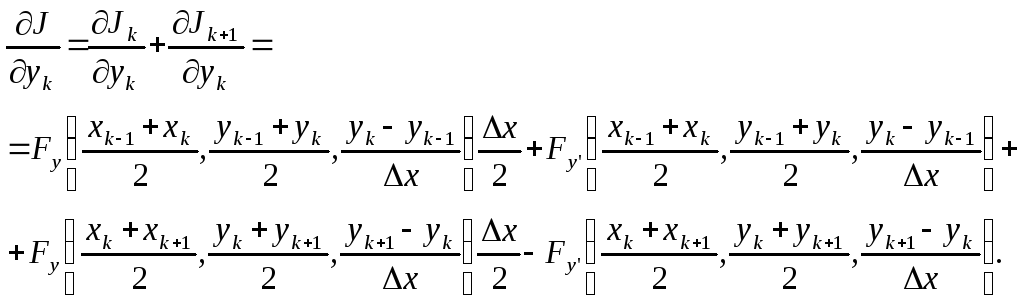(12.0)

После сокращения на x получим систему линейных алгебраических уравнений, которая своей структурой напоминает уравнение Эйлера (1.5):

(12.0)

Вместо F_y, которая фигурирует в уравнении Эйлера (1.5), в уравнении (12.4) – полусумма значенийF_yна интервалах, примыкающих к точкеx_k. ВместоdF_y'/dx– отношение разности величинF_y'справа и слева от точкиx_kк ширине интервалаx. Таким образом, (12.4) можно рассматривать как конечноразностный аналог уравнения Эйлера (1.5).

Аналогично выглядит конечноразностная аппроксимация уравнения Эйлера-Остроградского (4.6). Разобьём областьDна n участков вдоль осиOx: x(x₂x₁)/nи наm участков вдоль осиOy: y(y₂y₁)/m. Будем обозначать узлы сетки x_i,y_k. Граничные точки в этом примере будут x₀,x_n, y₀,y_m. МКР-аппроксимацияуравнения Эйлера-Остроградского (4.6) имеет вид

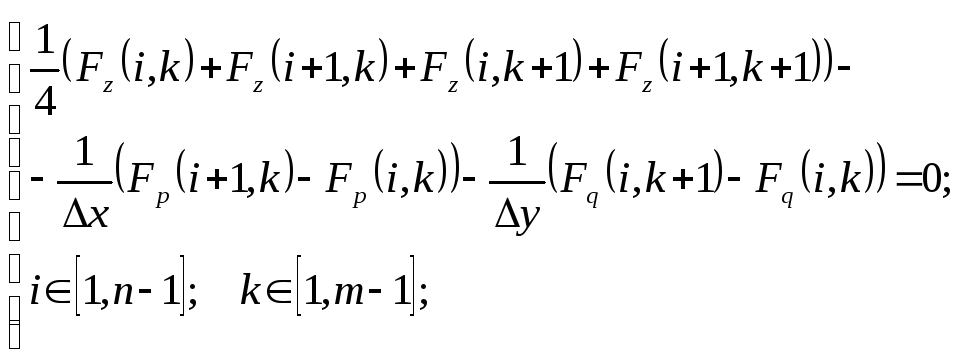(12.0)

где аргументы (i,k) для любой функции означают

.(12.0)

4. Примеры выполнения заданий

5. Пример 12a

Решить методом конечных разностей пример 1a. Сравнить решение с аналитическим.Построить графики.

Рис. 12.22. Решение примера 12a

Ответ.Для 10 интервалов разбиения система уравнений МКР имеет вид

(12.0)

при этом в 1-е уравнение входит y₀=1, а в 9-е уравнениеy₁₀=2. График экстремали показан на рис.12.1 сплошной красной линией, он практически сливается с теоретическим решением – штриховой синей линией.

6. Пример 12b

Решить МКР пример 4. Сравнить с решением МКЭ.Построить график.

Программу для этого примера напишем на основе программы для примера 4с использованием программы для примера12a. Введём исходные данные и вычислим частные производныеF_z,F_p,F_q.

Рис. 12.23. Решение примера 12b

Ответ.Для сетки 2040 система уравнений МКР вида (12.3) имеет вид

(12.0)

при этом входящие в (12.8) величины zприi=1,i=20,k=1,k=40 находятся из граничного условия в соответствующей точке. График экстремальной поверхности показан на рисунке в зоне вывода. Видно, что он очень похож на поверхность, построенной по МКЭ в главе4.